VERINA: Benchmarking Verifiable Code Generation

Large language models (LLMs) are increasingly integrated in software development, but ensuring correctness in LLM-generated code remains challenging and often requires costly manual review. Verifiable code generation -- jointly generating code, specifications, and proofs of code-specification alignment -- offers a promising path to address this limitation and further unleash LLMs' benefits in coding. Yet, there exists a significant gap in evaluation: current benchmarks often lack support for end-to-end verifiable code generation. In this paper, we introduce Verina (Verifiable Code Generation Arena), a high-quality benchmark enabling a comprehensive and modular evaluation of code, specification, and proof generation as well as their compositions. Verina consists of 189 manually curated coding tasks in Lean, with detailed problem descriptions, reference implementations, formal specifications, and extensive test suites. Our extensive evaluation of state-of-the-art LLMs reveals significant challenges in verifiable code generation, especially in proof generation, underscoring the need for improving LLM-based theorem provers in verification domains. The best model, OpenAI o4-mini, generates only 61.4% correct code, 51.0% sound and complete specifications, and 3.6% successful proofs, with one trial per task. We hope Verina will catalyze progress in verifiable code generation by providing a rigorous and comprehensive benchmark. We release our dataset on https://huggingface.co/datasets/sunblaze-ucb/verina and our evaluation code on https://github.com/sunblaze-ucb/verina.

Proving Olympiad Inequalities by Synergizing LLMs and Symbolic Reasoning

Large language models (LLMs) can prove mathematical theorems formally by generating proof steps (\textit{a.k.a.} tactics) within a proof system. However, the space of possible tactics is vast and complex, while the available training data for formal proofs is limited, posing a significant challenge to LLM-based tactic generation. To address this, we introduce a neuro-symbolic tactic generator that synergizes the mathematical intuition learned by LLMs with domain-specific insights encoded by symbolic methods. The key aspect of this integration is identifying which parts of mathematical reasoning are best suited to LLMs and which to symbolic methods. While the high-level idea of neuro-symbolic integration is broadly applicable to various mathematical problems, in this paper, we focus specifically on Olympiad inequalities (Figure~1). We analyze how humans solve these problems and distill the techniques into two types of tactics: (1) scaling, handled by symbolic methods, and (2) rewriting, handled by LLMs. In addition, we combine symbolic tools with LLMs to prune and rank the proof goals for efficient proof search. We evaluate our framework on 161 challenging inequalities from multiple mathematics competitions, achieving state-of-the-art performance and significantly outperforming existing LLM and symbolic approaches without requiring additional training data.

Spectral Journey: How Transformers Predict the Shortest Path

Decoder-only transformers lead to a step-change in capability of large language models. However, opinions are mixed as to whether they are really planning or reasoning. A path to making progress in this direction is to study the model's behavior in a setting with carefully controlled data. Then interpret the learned representations and reverse-engineer the computation performed internally. We study decoder-only transformer language models trained from scratch to predict shortest paths on simple, connected and undirected graphs. In this setting, the representations and the dynamics learned by the model are interpretable. We present three major results: (1) Two-layer decoder-only language models can learn to predict shortest paths on simple, connected graphs containing up to 10 nodes. (2) Models learn a graph embedding that is correlated with the spectral decomposition of the line graph. (3) Following the insights, we discover a novel approximate path-finding algorithm Spectral Line Navigator (SLN) that finds shortest path by greedily selecting nodes in the space of spectral embedding of the line graph.

Goedel-Prover: A Frontier Model for Open-Source Automated Theorem Proving

We introduce Goedel-Prover, an open-source large language model (LLM) that achieves the state-of-the-art (SOTA) performance in automated formal proof generation for mathematical problems. The key challenge in this field is the scarcity of formalized math statements and proofs, which we tackle in the following ways. We train statement formalizers to translate the natural language math problems from Numina into formal language (Lean 4), creating a dataset of 1.64 million formal statements. LLMs are used to check that the formal statements accurately preserve the content of the original natural language problems. We then iteratively build a large dataset of formal proofs by training a series of provers. Each prover succeeds in proving many statements that the previous ones could not, and these new proofs are added to the training set for the next prover. The final prover outperforms all existing open-source models in whole-proof generation. On the miniF2F benchmark, it achieves a 57.6% success rate (Pass@32), exceeding the previous best open-source model by 7.6%. On PutnamBench, Goedel-Prover successfully solves 7 problems (Pass@512), ranking first on the leaderboard. Furthermore, it generates 29.7K formal proofs for Lean Workbook problems, nearly doubling the 15.7K produced by earlier works.

Formal Mathematical Reasoning: A New Frontier in AI

AI for Mathematics (AI4Math) is not only intriguing intellectually but also crucial for AI-driven discovery in science, engineering, and beyond. Extensive efforts on AI4Math have mirrored techniques in NLP, in particular, training large language models on carefully curated math datasets in text form. As a complementary yet less explored avenue, formal mathematical reasoning is grounded in formal systems such as proof assistants, which can verify the correctness of reasoning and provide automatic feedback. In this position paper, we advocate for formal mathematical reasoning and argue that it is indispensable for advancing AI4Math to the next level. In recent years, we have seen steady progress in using AI to perform formal reasoning, including core tasks such as theorem proving and autoformalization, as well as emerging applications such as verifiable generation of code and hardware designs. However, significant challenges remain to be solved for AI to truly master mathematics and achieve broader impact. We summarize existing progress, discuss open challenges, and envision critical milestones to measure future success. At this inflection point for formal mathematical reasoning, we call on the research community to come together to drive transformative advancements in this field.

Autoformalizing Euclidean Geometry

Autoformalization involves automatically translating informal math into formal theorems and proofs that are machine-verifiable. Euclidean geometry provides an interesting and controllable domain for studying autoformalization. In this paper, we introduce a neuro-symbolic framework for autoformalizing Euclidean geometry, which combines domain knowledge, SMT solvers, and large language models (LLMs). One challenge in Euclidean geometry is that informal proofs rely on diagrams, leaving gaps in texts that are hard to formalize. To address this issue, we use theorem provers to fill in such diagrammatic information automatically, so that the LLM only needs to autoformalize the explicit textual steps, making it easier for the model. We also provide automatic semantic evaluation for autoformalized theorem statements. We construct LeanEuclid, an autoformalization benchmark consisting of problems from Euclid's Elements and the UniGeo dataset formalized in the Lean proof assistant. Experiments with GPT-4 and GPT-4V show the capability and limitations of state-of-the-art LLMs on autoformalizing geometry problems. The data and code are available at https://github.com/loganrjmurphy/LeanEuclid.

Towards Large Language Models as Copilots for Theorem Proving in Lean

Theorem proving is an important challenge for large language models (LLMs), as formal proofs can be checked rigorously by proof assistants such as Lean, leaving no room for hallucination. Existing LLM-based provers try to prove theorems in a fully autonomous mode without human intervention. In this mode, they struggle with novel and challenging theorems, for which human insights may be critical. In this paper, we explore LLMs as copilots that assist humans in proving theorems. We introduce Lean Copilot, a framework for running LLM inference in Lean. It enables programmers to build various LLM-based proof automation tools that integrate seamlessly into the workflow of Lean users. Using Lean Copilot, we build tools for suggesting proof steps (tactic suggestion), completing intermediate proof goals (proof search), and selecting relevant premises (premise selection) using LLMs. Users can use our pretrained models or bring their own ones that run either locally (with or without GPUs) or on the cloud. Experimental results demonstrate the effectiveness of our method in assisting humans and automating theorem proving process compared to existing rule-based proof automation in Lean. We open source all codes under a permissive MIT license to facilitate further research.

SciGLM: Training Scientific Language Models with Self-Reflective Instruction Annotation and Tuning

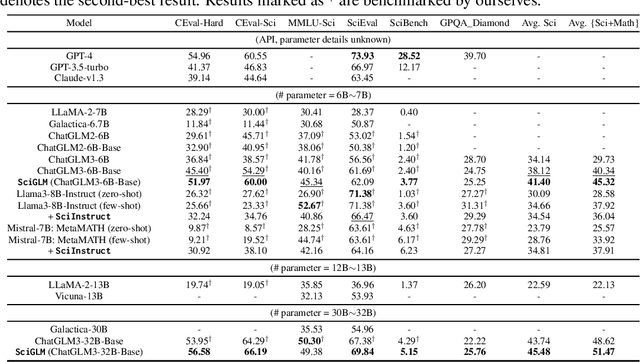
\label{sec:abstract} Large Language Models (LLMs) have shown promise in assisting scientific discovery. However, such applications are currently limited by LLMs' deficiencies in understanding intricate scientific concepts, deriving symbolic equations, and solving advanced numerical calculations. To bridge these gaps, we introduce SciGLM, a suite of scientific language models able to conduct college-level scientific reasoning. Central to our approach is a novel self-reflective instruction annotation framework to address the data scarcity challenge in the science domain. This framework leverages existing LLMs to generate step-by-step reasoning for unlabelled scientific questions, followed by a process of self-reflective critic-and-revise. Applying this framework, we curated SciInstruct, a diverse and high-quality dataset encompassing mathematics, physics, chemistry, and formal proofs. We fine-tuned the ChatGLM family of language models with SciInstruct, enhancing their capabilities in scientific and mathematical reasoning. Remarkably, SciGLM consistently improves both the base model (ChatGLM3-6B-Base) and larger-scale models (12B and 32B), without sacrificing the language understanding capabilities of the base model. This makes SciGLM a suitable foundational model to facilitate diverse scientific discovery tasks. For the benefit of the wider research community, we release SciInstruct, SciGLM, alongside a self-reflective framework and fine-tuning code at \url{https://github.com/THUDM/SciGLM}.

LeanDojo: Theorem Proving with Retrieval-Augmented Language Models

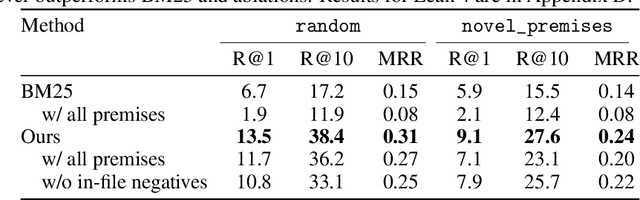
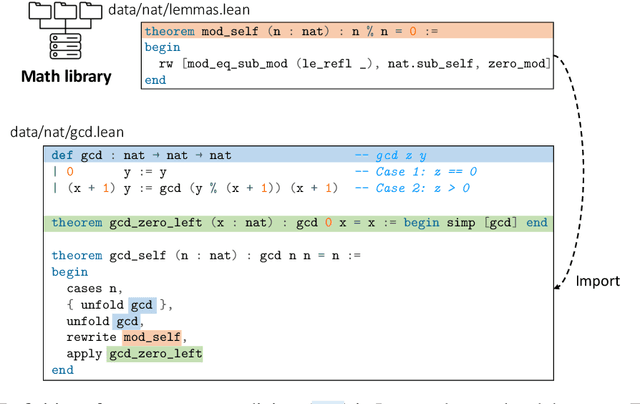
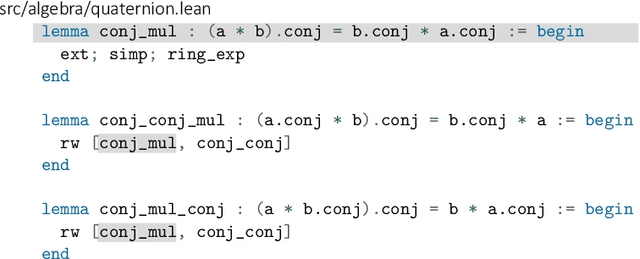
Large language models (LLMs) have shown promise in proving formal theorems using proof assistants such as Lean. However, existing methods are difficult to reproduce or build on, due to private code, data, and large compute requirements. This has created substantial barriers to research on machine learning methods for theorem proving. This paper removes these barriers by introducing LeanDojo: an open-source Lean playground consisting of toolkits, data, models, and benchmarks. LeanDojo extracts data from Lean and enables interaction with the proof environment programmatically. It contains fine-grained annotations of premises in proofs, providing valuable data for premise selection: a key bottleneck in theorem proving. Using this data, we develop ReProver (Retrieval-Augmented Prover): the first LLM-based prover that is augmented with retrieval for selecting premises from a vast math library. It is inexpensive and needs only one GPU week of training. Our retriever leverages LeanDojo's program analysis capability to identify accessible premises and hard negative examples, which makes retrieval much more effective. Furthermore, we construct a new benchmark consisting of 96,962 theorems and proofs extracted from Lean's math library. It features challenging data split requiring the prover to generalize to theorems relying on novel premises that are never used in training. We use this benchmark for training and evaluation, and experimental results demonstrate the effectiveness of ReProver over non-retrieval baselines and GPT-4. We thus provide the first set of open-source LLM-based theorem provers without any proprietary datasets and release it under a permissive MIT license to facilitate further research.

Infinite Photorealistic Worlds using Procedural Generation

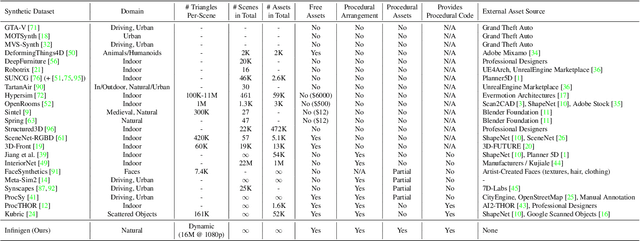
We introduce Infinigen, a procedural generator of photorealistic 3D scenes of the natural world. Infinigen is entirely procedural: every asset, from shape to texture, is generated from scratch via randomized mathematical rules, using no external source and allowing infinite variation and composition. Infinigen offers broad coverage of objects and scenes in the natural world including plants, animals, terrains, and natural phenomena such as fire, cloud, rain, and snow. Infinigen can be used to generate unlimited, diverse training data for a wide range of computer vision tasks including object detection, semantic segmentation, optical flow, and 3D reconstruction. We expect Infinigen to be a useful resource for computer vision research and beyond. Please visit https://infinigen.org for videos, code and pre-generated data.