Zhaoyu Li
Variational Bayesian Personalized Ranking
Mar 14, 2025Abstract:Recommendation systems have found extensive applications across diverse domains. However, the training data available typically comprises implicit feedback, manifested as user clicks and purchase behaviors, rather than explicit declarations of user preferences. This type of training data presents three main challenges for accurate ranking prediction: First, the unobservable nature of user preferences makes likelihood function modeling inherently difficult. Second, the resulting false positives (FP) and false negatives (FN) introduce noise into the learning process, disrupting parameter learning. Third, data bias arises as observed interactions tend to concentrate on a few popular items, exacerbating the feedback loop of popularity bias. To address these issues, we propose Variational BPR, a novel and easily implementable learning objective that integrates key components for enhancing collaborative filtering: likelihood optimization, noise reduction, and popularity debiasing. Our approach involves decomposing the pairwise loss under the ELBO-KL framework and deriving its variational lower bound to establish a manageable learning objective for approximate inference. Within this bound, we introduce an attention-based latent interest prototype contrastive mechanism, replacing instance-level contrastive learning, to effectively reduce noise from problematic samples. The process of deriving interest prototypes implicitly incorporates a flexible hard sample mining strategy, capable of simultaneously identifying hard positive and hard negative samples. Furthermore, we demonstrate that this hard sample mining strategy promotes feature distribution uniformity, thereby alleviating popularity bias. Empirically, we demonstrate the effectiveness of Variational BPR on popular backbone recommendation models. The code and data are available at: https://github.com/liubin06/VariationalBPR
Proving Olympiad Inequalities by Synergizing LLMs and Symbolic Reasoning
Feb 19, 2025



Abstract:Large language models (LLMs) can prove mathematical theorems formally by generating proof steps (\textit{a.k.a.} tactics) within a proof system. However, the space of possible tactics is vast and complex, while the available training data for formal proofs is limited, posing a significant challenge to LLM-based tactic generation. To address this, we introduce a neuro-symbolic tactic generator that synergizes the mathematical intuition learned by LLMs with domain-specific insights encoded by symbolic methods. The key aspect of this integration is identifying which parts of mathematical reasoning are best suited to LLMs and which to symbolic methods. While the high-level idea of neuro-symbolic integration is broadly applicable to various mathematical problems, in this paper, we focus specifically on Olympiad inequalities (Figure~1). We analyze how humans solve these problems and distill the techniques into two types of tactics: (1) scaling, handled by symbolic methods, and (2) rewriting, handled by LLMs. In addition, we combine symbolic tools with LLMs to prune and rank the proof goals for efficient proof search. We evaluate our framework on 161 challenging inequalities from multiple mathematics competitions, achieving state-of-the-art performance and significantly outperforming existing LLM and symbolic approaches without requiring additional training data.
Decoupling Training-Free Guided Diffusion by ADMM
Nov 18, 2024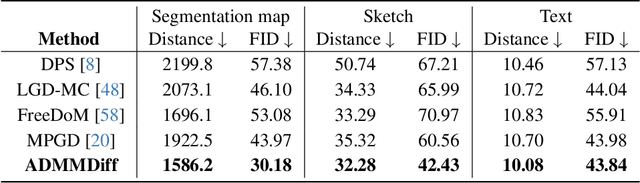
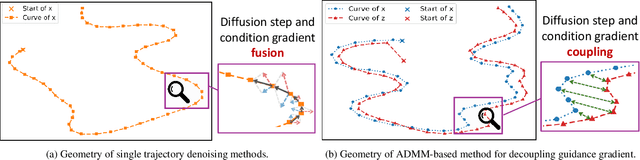


Abstract:In this paper, we consider the conditional generation problem by guiding off-the-shelf unconditional diffusion models with differentiable loss functions in a plug-and-play fashion. While previous research has primarily focused on balancing the unconditional diffusion model and the guided loss through a tuned weight hyperparameter, we propose a novel framework that distinctly decouples these two components. Specifically, we introduce two variables ${x}$ and ${z}$, to represent the generated samples governed by the unconditional generation model and the guidance function, respectively. This decoupling reformulates conditional generation into two manageable subproblems, unified by the constraint ${x} = {z}$. Leveraging this setup, we develop a new algorithm based on the Alternating Direction Method of Multipliers (ADMM) to adaptively balance these components. Additionally, we establish the equivalence between the diffusion reverse step and the proximal operator of ADMM and provide a detailed convergence analysis of our algorithm under certain mild assumptions. Our experiments demonstrate that our proposed method ADMMDiff consistently generates high-quality samples while ensuring strong adherence to the conditioning criteria. It outperforms existing methods across a range of conditional generation tasks, including image generation with various guidance and controllable motion synthesis.
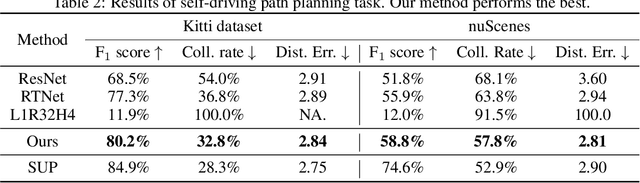
LogiCity: Advancing Neuro-Symbolic AI with Abstract Urban Simulation
Nov 01, 2024



Abstract:Recent years have witnessed the rapid development of Neuro-Symbolic (NeSy) AI systems, which integrate symbolic reasoning into deep neural networks. However, most of the existing benchmarks for NeSy AI fail to provide long-horizon reasoning tasks with complex multi-agent interactions. Furthermore, they are usually constrained by fixed and simplistic logical rules over limited entities, making them far from real-world complexities. To address these crucial gaps, we introduce LogiCity, the first simulator based on customizable first-order logic (FOL) for an urban-like environment with multiple dynamic agents. LogiCity models diverse urban elements using semantic and spatial concepts, such as IsAmbulance(X) and IsClose(X, Y). These concepts are used to define FOL rules that govern the behavior of various agents. Since the concepts and rules are abstractions, they can be universally applied to cities with any agent compositions, facilitating the instantiation of diverse scenarios. Besides, a key feature of LogiCity is its support for user-configurable abstractions, enabling customizable simulation complexities for logical reasoning. To explore various aspects of NeSy AI, LogiCity introduces two tasks, one features long-horizon sequential decision-making, and the other focuses on one-step visual reasoning, varying in difficulty and agent behaviors. Our extensive evaluation reveals the advantage of NeSy frameworks in abstract reasoning. Moreover, we highlight the significant challenges of handling more complex abstractions in long-horizon multi-agent scenarios or under high-dimensional, imbalanced data. With its flexible design, various features, and newly raised challenges, we believe LogiCity represents a pivotal step forward in advancing the next generation of NeSy AI. All the code and data are open-sourced at our website.
Neuro-symbolic Learning Yielding Logical Constraints
Oct 28, 2024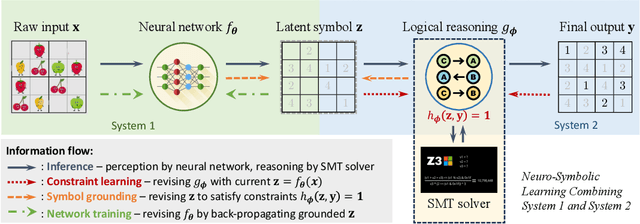
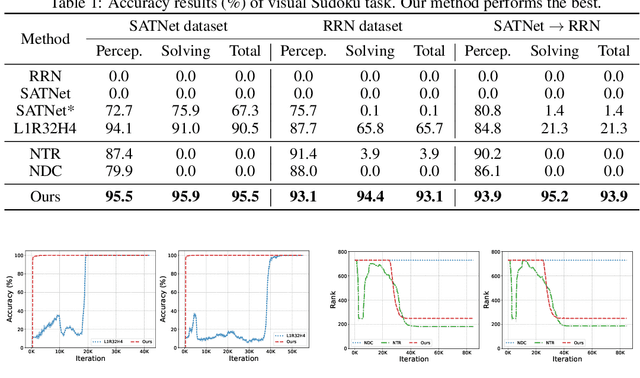
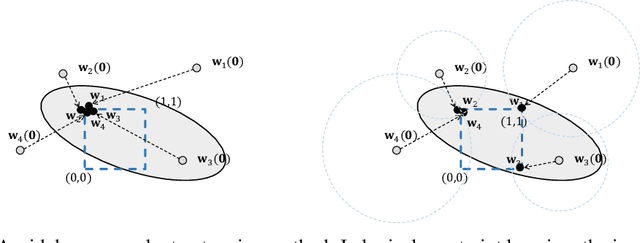
Abstract:Neuro-symbolic systems combine the abilities of neural perception and logical reasoning. However, end-to-end learning of neuro-symbolic systems is still an unsolved challenge. This paper proposes a natural framework that fuses neural network training, symbol grounding, and logical constraint synthesis into a coherent and efficient end-to-end learning process. The capability of this framework comes from the improved interactions between the neural and the symbolic parts of the system in both the training and inference stages. Technically, to bridge the gap between the continuous neural network and the discrete logical constraint, we introduce a difference-of-convex programming technique to relax the logical constraints while maintaining their precision. We also employ cardinality constraints as the language for logical constraint learning and incorporate a trust region method to avoid the degeneracy of logical constraint in learning. Both theoretical analyses and empirical evaluations substantiate the effectiveness of the proposed framework.
Autoformalize Mathematical Statements by Symbolic Equivalence and Semantic Consistency
Oct 28, 2024
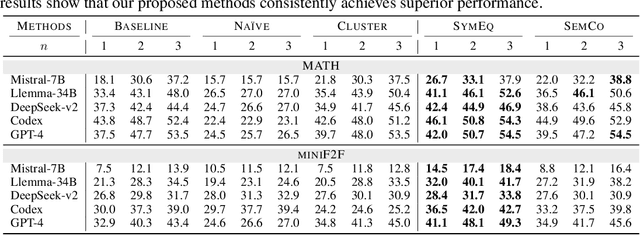

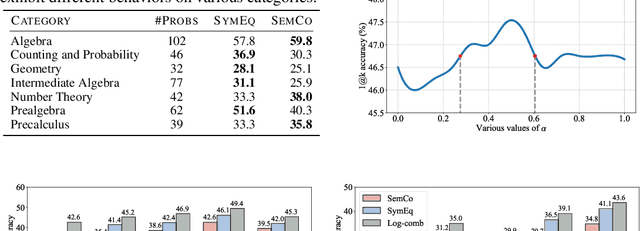
Abstract:Autoformalization, the task of automatically translating natural language descriptions into a formal language, poses a significant challenge across various domains, especially in mathematics. Recent advancements in large language models (LLMs) have unveiled their promising capabilities to formalize even competition-level math problems. However, we observe a considerable discrepancy between pass@1 and pass@k accuracies in LLM-generated formalizations. To address this gap, we introduce a novel framework that scores and selects the best result from k autoformalization candidates based on two complementary self-consistency methods: symbolic equivalence and semantic consistency. Elaborately, symbolic equivalence identifies the logical homogeneity among autoformalization candidates using automated theorem provers, and semantic consistency evaluates the preservation of the original meaning by informalizing the candidates and computing the similarity between the embeddings of the original and informalized texts. Our extensive experiments on the MATH and miniF2F datasets demonstrate that our approach significantly enhances autoformalization accuracy, achieving up to 0.22-1.35x relative improvements across various LLMs and baseline methods.
APPL: A Prompt Programming Language for Harmonious Integration of Programs and Large Language Model Prompts
Jun 19, 2024Abstract:Large Language Models (LLMs) have become increasingly capable of handling diverse tasks with the aid of well-crafted prompts and integration of external tools, but as task complexity rises, the workflow involving LLMs can be complicated and thus challenging to implement and maintain. To address this challenge, we propose APPL, A Prompt Programming Language that acts as a bridge between computer programs and LLMs, allowing seamless embedding of prompts into Python functions, and vice versa. APPL provides an intuitive and Python-native syntax, an efficient parallelized runtime with asynchronous semantics, and a tracing module supporting effective failure diagnosis and replaying without extra costs. We demonstrate that APPL programs are intuitive, concise, and efficient through three representative scenarios: Chain-of-Thought with self-consistency (CoT-SC), ReAct tool use agent, and multi-agent chat. Experiments on three parallelizable workflows further show that APPL can effectively parallelize independent LLM calls, with a significant speedup ratio that almost matches the estimation.
Autoformalizing Euclidean Geometry
May 27, 2024



Abstract:Autoformalization involves automatically translating informal math into formal theorems and proofs that are machine-verifiable. Euclidean geometry provides an interesting and controllable domain for studying autoformalization. In this paper, we introduce a neuro-symbolic framework for autoformalizing Euclidean geometry, which combines domain knowledge, SMT solvers, and large language models (LLMs). One challenge in Euclidean geometry is that informal proofs rely on diagrams, leaving gaps in texts that are hard to formalize. To address this issue, we use theorem provers to fill in such diagrammatic information automatically, so that the LLM only needs to autoformalize the explicit textual steps, making it easier for the model. We also provide automatic semantic evaluation for autoformalized theorem statements. We construct LeanEuclid, an autoformalization benchmark consisting of problems from Euclid's Elements and the UniGeo dataset formalized in the Lean proof assistant. Experiments with GPT-4 and GPT-4V show the capability and limitations of state-of-the-art LLMs on autoformalizing geometry problems. The data and code are available at https://github.com/loganrjmurphy/LeanEuclid.
Learning Reliable Logical Rules with SATNet
Oct 03, 2023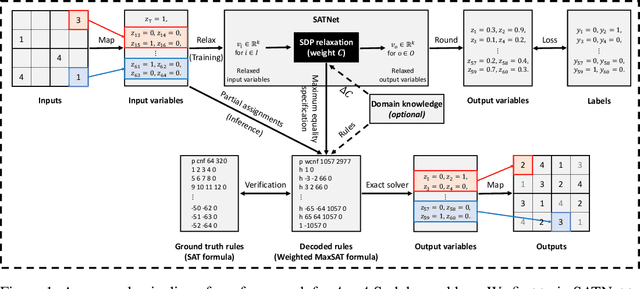
Abstract:Bridging logical reasoning and deep learning is crucial for advanced AI systems. In this work, we present a new framework that addresses this goal by generating interpretable and verifiable logical rules through differentiable learning, without relying on pre-specified logical structures. Our approach builds upon SATNet, a differentiable MaxSAT solver that learns the underlying rules from input-output examples. Despite its efficacy, the learned weights in SATNet are not straightforwardly interpretable, failing to produce human-readable rules. To address this, we propose a novel specification method called "maximum equality", which enables the interchangeability between the learned weights of SATNet and a set of propositional logical rules in weighted MaxSAT form. With the decoded weighted MaxSAT formula, we further introduce several effective verification techniques to validate it against the ground truth rules. Experiments on stream transformations and Sudoku problems show that our decoded rules are highly reliable: using exact solvers on them could achieve 100% accuracy, whereas the original SATNet fails to give correct solutions in many cases. Furthermore, we formally verify that our decoded logical rules are functionally equivalent to the ground truth ones.
G4SATBench: Benchmarking and Advancing SAT Solving with Graph Neural Networks
Sep 29, 2023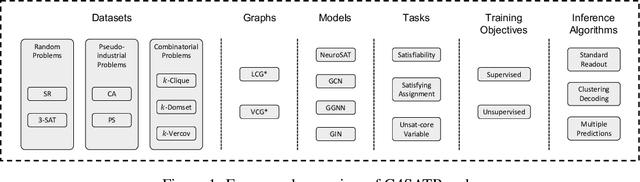

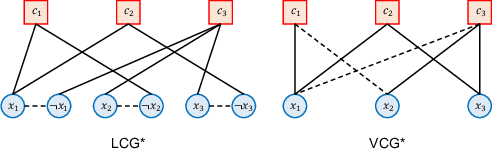
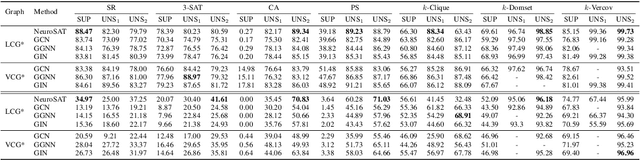
Abstract:Graph neural networks (GNNs) have recently emerged as a promising approach for solving the Boolean Satisfiability Problem (SAT), offering potential alternatives to traditional backtracking or local search SAT solvers. However, despite the growing volume of literature in this field, there remains a notable absence of a unified dataset and a fair benchmark to evaluate and compare existing approaches. To address this crucial gap, we present G4SATBench, the first benchmark study that establishes a comprehensive evaluation framework for GNN-based SAT solvers. In G4SATBench, we meticulously curate a large and diverse set of SAT datasets comprising 7 problems with 3 difficulty levels and benchmark a broad range of GNN models across various prediction tasks, training objectives, and inference algorithms. To explore the learning abilities and comprehend the strengths and limitations of GNN-based SAT solvers, we also compare their solving processes with the heuristics in search-based SAT solvers. Our empirical results provide valuable insights into the performance of GNN-based SAT solvers and further suggest that existing GNN models can effectively learn a solving strategy akin to greedy local search but struggle to learn backtracking search in the latent space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge