Chris J. Maddison
Measuring Scientific Capabilities of Language Models with a Systems Biology Dry Lab
Jul 02, 2025
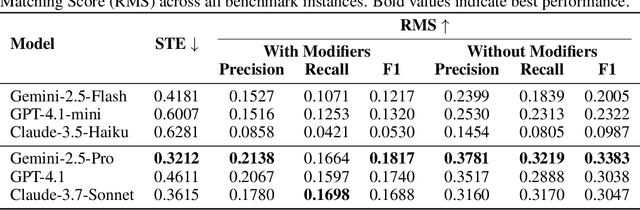
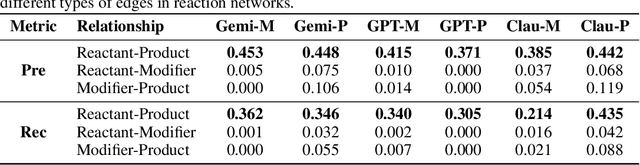
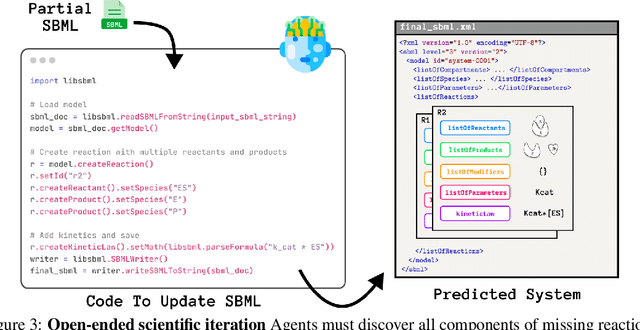
Abstract:Designing experiments and result interpretations are core scientific competencies, particularly in biology, where researchers perturb complex systems to uncover the underlying systems. Recent efforts to evaluate the scientific capabilities of large language models (LLMs) fail to test these competencies because wet-lab experimentation is prohibitively expensive: in expertise, time and equipment. We introduce SciGym, a first-in-class benchmark that assesses LLMs' iterative experiment design and analysis abilities in open-ended scientific discovery tasks. SciGym overcomes the challenge of wet-lab costs by running a dry lab of biological systems. These models, encoded in Systems Biology Markup Language, are efficient for generating simulated data, making them ideal testbeds for experimentation on realistically complex systems. We evaluated six frontier LLMs on 137 small systems, and released a total of 350 systems. Our evaluation shows that while more capable models demonstrated superior performance, all models' performance declined significantly as system complexity increased, suggesting substantial room for improvement in the scientific capabilities of LLM agents.
BioReason: Incentivizing Multimodal Biological Reasoning within a DNA-LLM Model
May 29, 2025



Abstract:Unlocking deep, interpretable biological reasoning from complex genomic data is a major AI challenge hindering scientific discovery. Current DNA foundation models, despite strong sequence representation, struggle with multi-step reasoning and lack inherent transparent, biologically intuitive explanations. We introduce BioReason, a pioneering architecture that, for the first time, deeply integrates a DNA foundation model with a Large Language Model (LLM). This novel connection enables the LLM to directly process and reason with genomic information as a fundamental input, fostering a new form of multimodal biological understanding. BioReason's sophisticated multi-step reasoning is developed through supervised fine-tuning and targeted reinforcement learning, guiding the system to generate logical, biologically coherent deductions. On biological reasoning benchmarks including KEGG-based disease pathway prediction - where accuracy improves from 88% to 97% - and variant effect prediction, BioReason demonstrates an average 15% performance gain over strong single-modality baselines. BioReason reasons over unseen biological entities and articulates decision-making through interpretable, step-by-step biological traces, offering a transformative approach for AI in biology that enables deeper mechanistic insights and accelerates testable hypothesis generation from genomic data. Data, code, and checkpoints are publicly available at https://github.com/bowang-lab/BioReason
Enumerate-Conjecture-Prove: Formally Solving Answer-Construction Problems in Math Competitions
May 24, 2025Abstract:Mathematical reasoning lies at the heart of artificial intelligence, underpinning applications in education, program verification, and research-level mathematical discovery. Mathematical competitions, in particular, present two challenging problem types: theorem-proving, requiring rigorous proofs of stated conclusions, and answer-construction, involving hypothesizing and formally verifying mathematical objects. Large Language Models (LLMs) effectively generate creative candidate answers but struggle with formal verification, while symbolic provers ensure rigor but cannot efficiently handle creative conjecture generation. We introduce the Enumerate-Conjecture-Prove (ECP) framework, a modular neuro-symbolic method integrating LLM-based enumeration and pattern-driven conjecturing with formal theorem proving. We present ConstructiveBench, a dataset of 3,431 answer-construction problems in various math competitions with verified Lean formalizations. On the ConstructiveBench dataset, ECP improves the accuracy of answer construction from the Chain-of-Thought (CoT) baseline of 14.54% to 45.06% with the gpt-4.1-mini model. Moreover, combining with ECP's constructed answers, the state-of-the-art DeepSeek-Prover-V2-7B model generates correct proofs for 858 of the 3,431 constructive problems in Lean, achieving 25.01% accuracy, compared to 9.86% for symbolic-only baselines. Our code and dataset are publicly available at GitHub and HuggingFace, respectively.
Reasoning to Learn from Latent Thoughts
Mar 24, 2025Abstract:Compute scaling for language model (LM) pretraining has outpaced the growth of human-written texts, leading to concerns that data will become the bottleneck to LM scaling. To continue scaling pretraining in this data-constrained regime, we propose that explicitly modeling and inferring the latent thoughts that underlie the text generation process can significantly improve pretraining data efficiency. Intuitively, our approach views web text as the compressed final outcome of a verbose human thought process and that the latent thoughts contain important contextual knowledge and reasoning steps that are critical to data-efficient learning. We empirically demonstrate the effectiveness of our approach through data-constrained continued pretraining for math. We first show that synthetic data approaches to inferring latent thoughts significantly improve data efficiency, outperforming training on the same amount of raw data (5.7\% $\rightarrow$ 25.4\% on MATH). Furthermore, we demonstrate latent thought inference without a strong teacher, where an LM bootstraps its own performance by using an EM algorithm to iteratively improve the capability of the trained LM and the quality of thought-augmented pretraining data. We show that a 1B LM can bootstrap its performance across at least three iterations and significantly outperform baselines trained on raw data, with increasing gains from additional inference compute when performing the E-step. The gains from inference scaling and EM iterations suggest new opportunities for scaling data-constrained pretraining.
On the Efficiency of ERM in Feature Learning
Nov 18, 2024Abstract:Given a collection of feature maps indexed by a set $\mathcal{T}$, we study the performance of empirical risk minimization (ERM) on regression problems with square loss over the union of the linear classes induced by these feature maps. This setup aims at capturing the simplest instance of feature learning, where the model is expected to jointly learn from the data an appropriate feature map and a linear predictor. We start by studying the asymptotic quantiles of the excess risk of sequences of empirical risk minimizers. Remarkably, we show that when the set $\mathcal{T}$ is not too large and when there is a unique optimal feature map, these quantiles coincide, up to a factor of two, with those of the excess risk of the oracle procedure, which knows a priori this optimal feature map and deterministically outputs an empirical risk minimizer from the associated optimal linear class. We complement this asymptotic result with a non-asymptotic analysis that quantifies the decaying effect of the global complexity of the set $\mathcal{T}$ on the excess risk of ERM, and relates it to the size of the sublevel sets of the suboptimality of the feature maps. As an application of our results, we obtain new guarantees on the performance of the best subset selection procedure in sparse linear regression under general assumptions.
End-To-End Causal Effect Estimation from Unstructured Natural Language Data
Jul 09, 2024
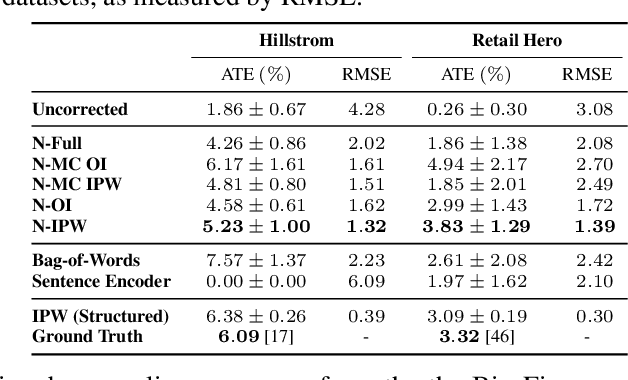


Abstract:Knowing the effect of an intervention is critical for human decision-making, but current approaches for causal effect estimation rely on manual data collection and structuring, regardless of the causal assumptions. This increases both the cost and time-to-completion for studies. We show how large, diverse observational text data can be mined with large language models (LLMs) to produce inexpensive causal effect estimates under appropriate causal assumptions. We introduce NATURAL, a novel family of causal effect estimators built with LLMs that operate over datasets of unstructured text. Our estimators use LLM conditional distributions (over variables of interest, given the text data) to assist in the computation of classical estimators of causal effect. We overcome a number of technical challenges to realize this idea, such as automating data curation and using LLMs to impute missing information. We prepare six (two synthetic and four real) observational datasets, paired with corresponding ground truth in the form of randomized trials, which we used to systematically evaluate each step of our pipeline. NATURAL estimators demonstrate remarkable performance, yielding causal effect estimates that fall within 3 percentage points of their ground truth counterparts, including on real-world Phase 3/4 clinical trials. Our results suggest that unstructured text data is a rich source of causal effect information, and NATURAL is a first step towards an automated pipeline to tap this resource.
APPL: A Prompt Programming Language for Harmonious Integration of Programs and Large Language Model Prompts
Jun 19, 2024Abstract:Large Language Models (LLMs) have become increasingly capable of handling diverse tasks with the aid of well-crafted prompts and integration of external tools, but as task complexity rises, the workflow involving LLMs can be complicated and thus challenging to implement and maintain. To address this challenge, we propose APPL, A Prompt Programming Language that acts as a bridge between computer programs and LLMs, allowing seamless embedding of prompts into Python functions, and vice versa. APPL provides an intuitive and Python-native syntax, an efficient parallelized runtime with asynchronous semantics, and a tracing module supporting effective failure diagnosis and replaying without extra costs. We demonstrate that APPL programs are intuitive, concise, and efficient through three representative scenarios: Chain-of-Thought with self-consistency (CoT-SC), ReAct tool use agent, and multi-agent chat. Experiments on three parallelizable workflows further show that APPL can effectively parallelize independent LLM calls, with a significant speedup ratio that almost matches the estimation.
Minimax Linear Regression under the Quantile Risk
Jun 17, 2024Abstract:We study the problem of designing minimax procedures in linear regression under the quantile risk. We start by considering the realizable setting with independent Gaussian noise, where for any given noise level and distribution of inputs, we obtain the exact minimax quantile risk for a rich family of error functions and establish the minimaxity of OLS. This improves on the known lower bounds for the special case of square error, and provides us with a lower bound on the minimax quantile risk over larger sets of distributions. Under the square error and a fourth moment assumption on the distribution of inputs, we show that this lower bound is tight over a larger class of problems. Specifically, we prove a matching upper bound on the worst-case quantile risk of a variant of the recently proposed min-max regression procedure, thereby establishing its minimaxity, up to absolute constants. We illustrate the usefulness of our approach by extending this result to all $p$-th power error functions for $p \in (2, \infty)$. Along the way, we develop a generic analogue to the classical Bayesian method for lower bounding the minimax risk when working with the quantile risk, as well as a tight characterization of the quantiles of the smallest eigenvalue of the sample covariance matrix.
Out-Of-Context Prompting Boosts Fairness and Robustness in Large Language Model Predictions
Jun 11, 2024Abstract:Frontier Large Language Models (LLMs) are increasingly being deployed for high-stakes decision-making. On the other hand, these models are still consistently making predictions that contradict users' or society's expectations, e.g., hallucinating, or discriminating. Thus, it is important that we develop test-time strategies to improve their trustworthiness. Inspired by prior work, we leverage causality as a tool to formally encode two aspects of trustworthiness in LLMs: fairness and robustness. Under this perspective, existing test-time solutions explicitly instructing the model to be fair or robust implicitly depend on the LLM's causal reasoning capabilities. In this work, we explore the opposite approach. Instead of explicitly asking the LLM for trustworthiness, we design prompts to encode the underlying causal inference algorithm that will, by construction, result in more trustworthy predictions. Concretely, we propose out-of-context prompting as a test-time solution to encourage fairness and robustness in LLMs. Out-of-context prompting leverages the user's prior knowledge of the task's causal model to apply (random) counterfactual transformations and improve the model's trustworthiness. Empirically, we show that out-of-context prompting consistently improves the fairness and robustness of frontier LLMs across five different benchmark datasets without requiring additional data, finetuning or pre-training.
Finding Optimally Robust Data Mixtures via Concave Maximization
Jun 03, 2024Abstract:Training on mixtures of data distributions is now common in many modern machine learning pipelines, useful for performing well on several downstream tasks. Group distributionally robust optimization (group DRO) is one popular way to learn mixture weights for training a specific model class, but group DRO methods suffer for non-linear models due to non-convex loss functions and when the models are non-parametric. We address these challenges by proposing to solve a more general DRO problem, giving a method we call MixMax. MixMax selects mixture weights by maximizing a particular concave objective with entropic mirror ascent, and, crucially, we prove that optimally fitting this mixture distribution over the set of bounded predictors returns a group DRO optimal model. Experimentally, we tested MixMax on a sequence modeling task with transformers and on a variety of non-parametric learning problems. In all instances MixMax matched or outperformed the standard data mixing and group DRO baselines, and in particular, MixMax improved the performance of XGBoost over the only baseline, data balancing, for variations of the ACSIncome and CelebA annotations datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge