$τ^2$-Bench: Evaluating Conversational Agents in a Dual-Control Environment

Existing benchmarks for conversational AI agents simulate single-control environments, where only the AI agent can use tools to interact with the world, while the user remains a passive information provider. This differs from real-world scenarios like technical support, where users need to actively participate in modifying the state of the (shared) world. In order to address this gap, we introduce $\tau^2$-bench, with four key contributions: 1) A novel Telecom dual-control domain modeled as a Dec-POMDP, where both agent and user make use of tools to act in a shared, dynamic environment that tests both agent coordination and communication, 2) A compositional task generator that programmatically creates diverse, verifiable tasks from atomic components, ensuring domain coverage and controlled complexity, 3) A reliable user simulator tightly coupled with the environment, whose behavior is constrained by tools and observable states, improving simulation fidelity, 4) Fine-grained analysis of agent performance through multiple ablations including separating errors arising from reasoning vs communication/coordination. In particular, our experiments show significant performance drops when agents shift from no-user to dual-control, highlighting the challenges of guiding users. Overall, $\tau^2$-bench provides a controlled testbed for agents that must both reason effectively and guide user actions.

Extracting Interpretable Logic Rules from Graph Neural Networks

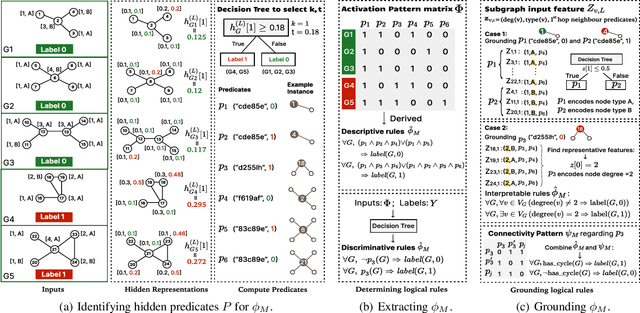
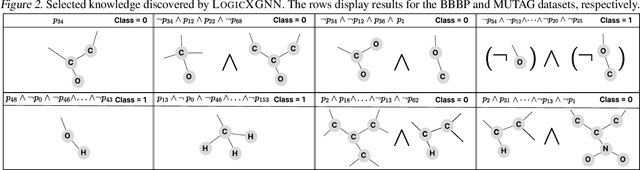
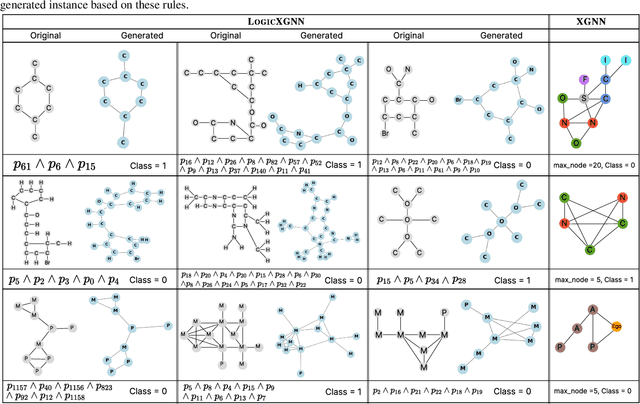
Graph neural networks (GNNs) operate over both input feature spaces and combinatorial graph structures, making it challenging to understand the rationale behind their predictions. As GNNs gain widespread popularity and demonstrate success across various domains, such as drug discovery, studying their interpretability has become a critical task. To address this, many explainability methods have been proposed, with recent efforts shifting from instance-specific explanations to global concept-based explainability. However, these approaches face several limitations, such as relying on predefined concepts and explaining only a limited set of patterns. To address this, we propose a novel framework, LOGICXGNN, for extracting interpretable logic rules from GNNs. LOGICXGNN is model-agnostic, efficient, and data-driven, eliminating the need for predefined concepts. More importantly, it can serve as a rule-based classifier and even outperform the original neural models. Its interpretability facilitates knowledge discovery, as demonstrated by its ability to extract detailed and accurate chemistry knowledge that is often overlooked by existing methods. Another key advantage of LOGICXGNN is its ability to generate new graph instances in a controlled and transparent manner, offering significant potential for applications such as drug design. We empirically demonstrate these merits through experiments on real-world datasets such as MUTAG and BBBP.

Learning Interpretable Logic Rules from Deep Vision Models

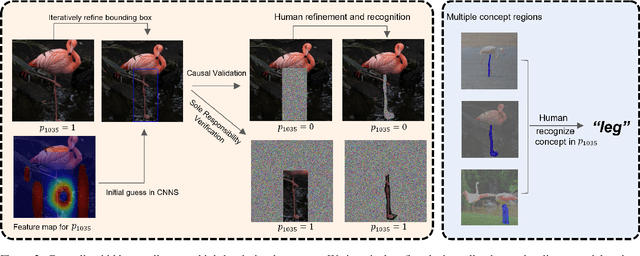
We propose a general framework called VisionLogic to extract interpretable logic rules from deep vision models, with a focus on image classification tasks. Given any deep vision model that uses a fully connected layer as the output head, VisionLogic transforms neurons in the last layer into predicates and grounds them into vision concepts using causal validation. In this way, VisionLogic can provide local explanations for single images and global explanations for specific classes in the form of logic rules. Compared to existing interpretable visualization tools such as saliency maps, VisionLogic addresses several key challenges, including the lack of causal explanations, overconfidence in visualizations, and ambiguity in interpretation. VisionLogic also facilitates the study of visual concepts encoded by predicates, particularly how they behave under perturbation -- an area that remains underexplored in the field of hidden semantics. Apart from providing better visual explanations and insights into the visual concepts learned by the model, we show that VisionLogic retains most of the neural network's discriminative power in an interpretable and transparent manner. We envision it as a bridge between complex model behavior and human-understandable explanations, providing trustworthy and actionable insights for real-world applications.

Proving Olympiad Inequalities by Synergizing LLMs and Symbolic Reasoning

Large language models (LLMs) can prove mathematical theorems formally by generating proof steps (\textit{a.k.a.} tactics) within a proof system. However, the space of possible tactics is vast and complex, while the available training data for formal proofs is limited, posing a significant challenge to LLM-based tactic generation. To address this, we introduce a neuro-symbolic tactic generator that synergizes the mathematical intuition learned by LLMs with domain-specific insights encoded by symbolic methods. The key aspect of this integration is identifying which parts of mathematical reasoning are best suited to LLMs and which to symbolic methods. While the high-level idea of neuro-symbolic integration is broadly applicable to various mathematical problems, in this paper, we focus specifically on Olympiad inequalities (Figure~1). We analyze how humans solve these problems and distill the techniques into two types of tactics: (1) scaling, handled by symbolic methods, and (2) rewriting, handled by LLMs. In addition, we combine symbolic tools with LLMs to prune and rank the proof goals for efficient proof search. We evaluate our framework on 161 challenging inequalities from multiple mathematics competitions, achieving state-of-the-art performance and significantly outperforming existing LLM and symbolic approaches without requiring additional training data.

RAG-Verus: Repository-Level Program Verification with LLMs using Retrieval Augmented Generation

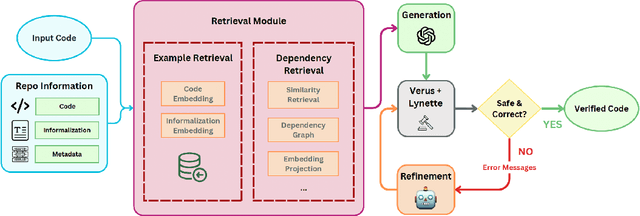
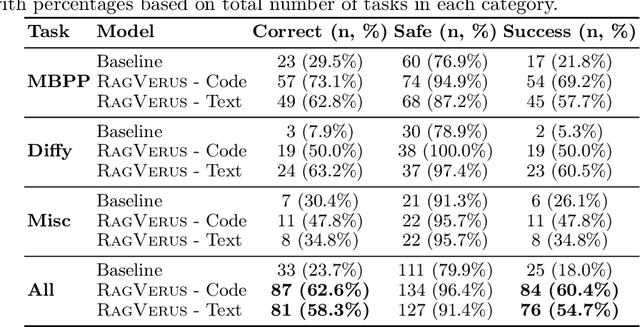
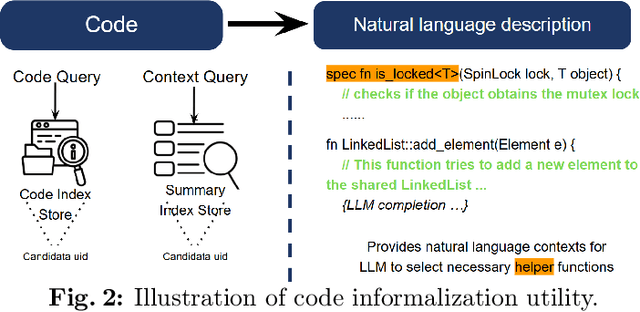
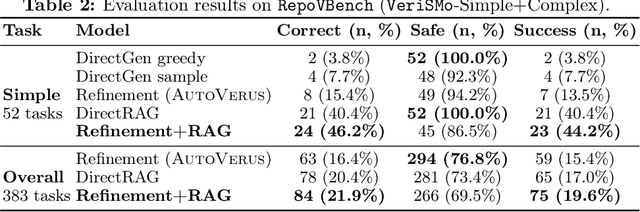
Scaling automated formal verification to real-world projects requires resolving cross-module dependencies and global contexts, which are challenges overlooked by existing function-centric methods. We introduce RagVerus, a framework that synergizes retrieval-augmented generation with context-aware prompting to automate proof synthesis for multi-module repositories, achieving a 27% relative improvement on our novel RepoVBench benchmark -- the first repository-level dataset for Verus with 383 proof completion tasks. RagVerus triples proof pass rates on existing benchmarks under constrained language model budgets, demonstrating a scalable and sample-efficient verification.

Decoding Interpretable Logic Rules from Neural Networks

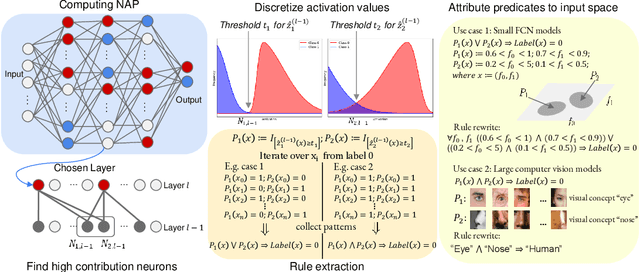
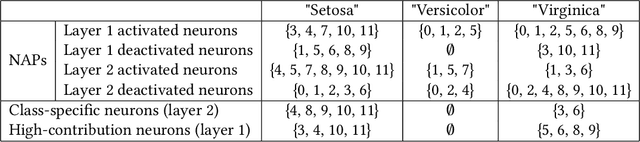
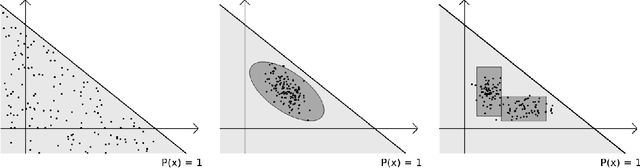
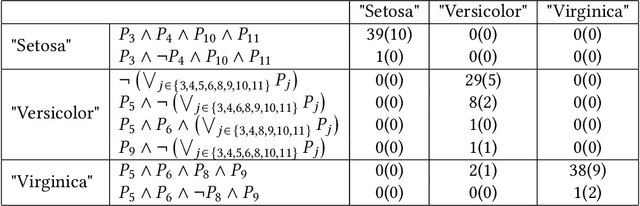
As deep neural networks continue to excel across various domains, their black-box nature has raised concerns about transparency and trust. In particular, interpretability has become increasingly essential for applications that demand high safety and knowledge rigor, such as drug discovery, autonomous driving, and genomics. However, progress in understanding even the simplest deep neural networks - such as fully connected networks - has been limited, despite their role as foundational elements in state-of-the-art models like ResNet and Transformer. In this paper, we address this challenge by introducing NeuroLogic, a novel approach for decoding interpretable logic rules from neural networks. NeuroLogic leverages neural activation patterns to capture the model's critical decision-making processes, translating them into logical rules represented by hidden predicates. Thanks to its flexible design in the grounding phase, NeuroLogic can be adapted to a wide range of neural networks. For simple fully connected neural networks, hidden predicates can be grounded in certain split patterns of original input features to derive decision-tree-like rules. For large, complex vision neural networks, NeuroLogic grounds hidden predicates into high-level visual concepts that are understandable to humans. Our empirical study demonstrates that NeuroLogic can extract global and interpretable rules from state-of-the-art models such as ResNet, a task at which existing work struggles. We believe NeuroLogic can help pave the way for understanding the black-box nature of neural networks.

Decoupling Training-Free Guided Diffusion by ADMM

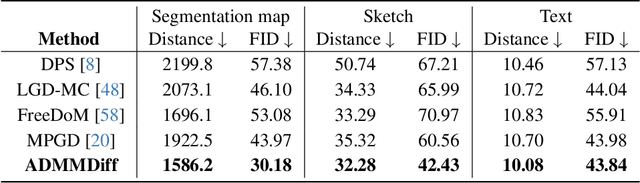
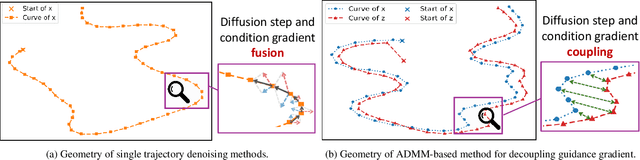
In this paper, we consider the conditional generation problem by guiding off-the-shelf unconditional diffusion models with differentiable loss functions in a plug-and-play fashion. While previous research has primarily focused on balancing the unconditional diffusion model and the guided loss through a tuned weight hyperparameter, we propose a novel framework that distinctly decouples these two components. Specifically, we introduce two variables ${x}$ and ${z}$, to represent the generated samples governed by the unconditional generation model and the guidance function, respectively. This decoupling reformulates conditional generation into two manageable subproblems, unified by the constraint ${x} = {z}$. Leveraging this setup, we develop a new algorithm based on the Alternating Direction Method of Multipliers (ADMM) to adaptively balance these components. Additionally, we establish the equivalence between the diffusion reverse step and the proximal operator of ADMM and provide a detailed convergence analysis of our algorithm under certain mild assumptions. Our experiments demonstrate that our proposed method ADMMDiff consistently generates high-quality samples while ensuring strong adherence to the conditioning criteria. It outperforms existing methods across a range of conditional generation tasks, including image generation with various guidance and controllable motion synthesis.

LogiCity: Advancing Neuro-Symbolic AI with Abstract Urban Simulation

Recent years have witnessed the rapid development of Neuro-Symbolic (NeSy) AI systems, which integrate symbolic reasoning into deep neural networks. However, most of the existing benchmarks for NeSy AI fail to provide long-horizon reasoning tasks with complex multi-agent interactions. Furthermore, they are usually constrained by fixed and simplistic logical rules over limited entities, making them far from real-world complexities. To address these crucial gaps, we introduce LogiCity, the first simulator based on customizable first-order logic (FOL) for an urban-like environment with multiple dynamic agents. LogiCity models diverse urban elements using semantic and spatial concepts, such as IsAmbulance(X) and IsClose(X, Y). These concepts are used to define FOL rules that govern the behavior of various agents. Since the concepts and rules are abstractions, they can be universally applied to cities with any agent compositions, facilitating the instantiation of diverse scenarios. Besides, a key feature of LogiCity is its support for user-configurable abstractions, enabling customizable simulation complexities for logical reasoning. To explore various aspects of NeSy AI, LogiCity introduces two tasks, one features long-horizon sequential decision-making, and the other focuses on one-step visual reasoning, varying in difficulty and agent behaviors. Our extensive evaluation reveals the advantage of NeSy frameworks in abstract reasoning. Moreover, we highlight the significant challenges of handling more complex abstractions in long-horizon multi-agent scenarios or under high-dimensional, imbalanced data. With its flexible design, various features, and newly raised challenges, we believe LogiCity represents a pivotal step forward in advancing the next generation of NeSy AI. All the code and data are open-sourced at our website.

Library Learning Doesn't: The Curious Case of the Single-Use "Library"

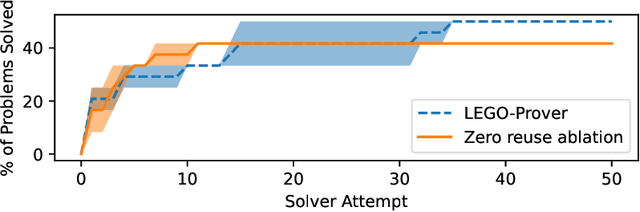
Advances in Large Language Models (LLMs) have spurred a wave of LLM library learning systems for mathematical reasoning. These systems aim to learn a reusable library of tools, such as formal Isabelle lemmas or Python programs that are tailored to a family of tasks. Many of these systems are inspired by the human structuring of knowledge into reusable and extendable concepts, but do current methods actually learn reusable libraries of tools? We study two library learning systems for mathematics which both reported increased accuracy: LEGO-Prover and TroVE. We find that function reuse is extremely infrequent on miniF2F and MATH. Our followup ablation experiments suggest that, rather than reuse, self-correction and self-consistency are the primary drivers of the observed performance gains. Our code and data are available at https://github.com/ikb-a/curious-case

APPL: A Prompt Programming Language for Harmonious Integration of Programs and Large Language Model Prompts

Large Language Models (LLMs) have become increasingly capable of handling diverse tasks with the aid of well-crafted prompts and integration of external tools, but as task complexity rises, the workflow involving LLMs can be complicated and thus challenging to implement and maintain. To address this challenge, we propose APPL, A Prompt Programming Language that acts as a bridge between computer programs and LLMs, allowing seamless embedding of prompts into Python functions, and vice versa. APPL provides an intuitive and Python-native syntax, an efficient parallelized runtime with asynchronous semantics, and a tracing module supporting effective failure diagnosis and replaying without extra costs. We demonstrate that APPL programs are intuitive, concise, and efficient through three representative scenarios: Chain-of-Thought with self-consistency (CoT-SC), ReAct tool use agent, and multi-agent chat. Experiments on three parallelizable workflows further show that APPL can effectively parallelize independent LLM calls, with a significant speedup ratio that almost matches the estimation.