Learning Interpretable Logic Rules from Deep Vision Models

We propose a general framework called VisionLogic to extract interpretable logic rules from deep vision models, with a focus on image classification tasks. Given any deep vision model that uses a fully connected layer as the output head, VisionLogic transforms neurons in the last layer into predicates and grounds them into vision concepts using causal validation. In this way, VisionLogic can provide local explanations for single images and global explanations for specific classes in the form of logic rules. Compared to existing interpretable visualization tools such as saliency maps, VisionLogic addresses several key challenges, including the lack of causal explanations, overconfidence in visualizations, and ambiguity in interpretation. VisionLogic also facilitates the study of visual concepts encoded by predicates, particularly how they behave under perturbation -- an area that remains underexplored in the field of hidden semantics. Apart from providing better visual explanations and insights into the visual concepts learned by the model, we show that VisionLogic retains most of the neural network's discriminative power in an interpretable and transparent manner. We envision it as a bridge between complex model behavior and human-understandable explanations, providing trustworthy and actionable insights for real-world applications.

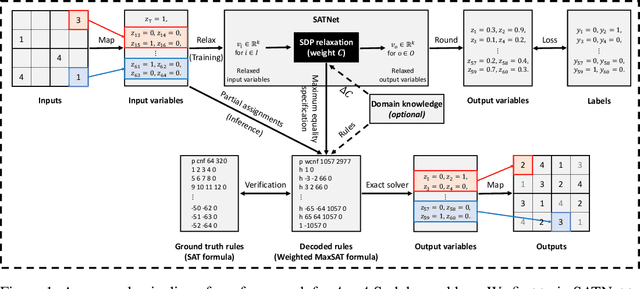
Learning Reliable Logical Rules with SATNet

Bridging logical reasoning and deep learning is crucial for advanced AI systems. In this work, we present a new framework that addresses this goal by generating interpretable and verifiable logical rules through differentiable learning, without relying on pre-specified logical structures. Our approach builds upon SATNet, a differentiable MaxSAT solver that learns the underlying rules from input-output examples. Despite its efficacy, the learned weights in SATNet are not straightforwardly interpretable, failing to produce human-readable rules. To address this, we propose a novel specification method called "maximum equality", which enables the interchangeability between the learned weights of SATNet and a set of propositional logical rules in weighted MaxSAT form. With the decoded weighted MaxSAT formula, we further introduce several effective verification techniques to validate it against the ground truth rules. Experiments on stream transformations and Sudoku problems show that our decoded rules are highly reliable: using exact solvers on them could achieve 100% accuracy, whereas the original SATNet fails to give correct solutions in many cases. Furthermore, we formally verify that our decoded logical rules are functionally equivalent to the ground truth ones.