Fast T2T: Optimization Consistency Speeds Up Diffusion-Based Training-to-Testing Solving for Combinatorial Optimization

Diffusion models have recently advanced Combinatorial Optimization (CO) as a powerful backbone for neural solvers. However, their iterative sampling process requiring denoising across multiple noise levels incurs substantial overhead. We propose to learn direct mappings from different noise levels to the optimal solution for a given instance, facilitating high-quality generation with minimal shots. This is achieved through an optimization consistency training protocol, which, for a given instance, minimizes the difference among samples originating from varying generative trajectories and time steps relative to the optimal solution. The proposed model enables fast single-step solution generation while retaining the option of multi-step sampling to trade for sampling quality, which offers a more effective and efficient alternative backbone for neural solvers. In addition, within the training-to-testing (T2T) framework, to bridge the gap between training on historical instances and solving new instances, we introduce a novel consistency-based gradient search scheme during the test stage, enabling more effective exploration of the solution space learned during training. It is achieved by updating the latent solution probabilities under objective gradient guidance during the alternation of noise injection and denoising steps. We refer to this model as Fast T2T. Extensive experiments on two popular tasks, the Traveling Salesman Problem (TSP) and Maximal Independent Set (MIS), demonstrate the superiority of Fast T2T regarding both solution quality and efficiency, even outperforming LKH given limited time budgets. Notably, Fast T2T with merely one-step generation and one-step gradient search can mostly outperform the SOTA diffusion-based counterparts that require hundreds of steps, while achieving tens of times speedup.

GMTR: Graph Matching Transformers

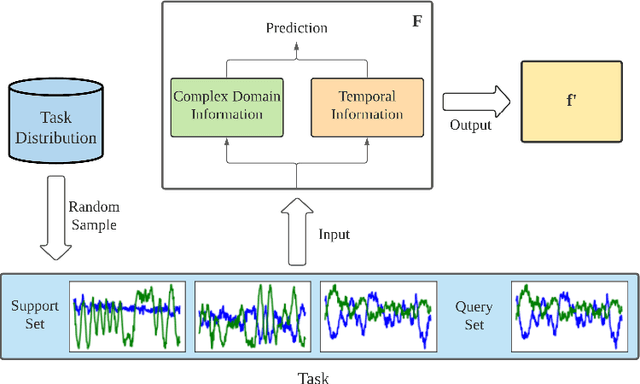
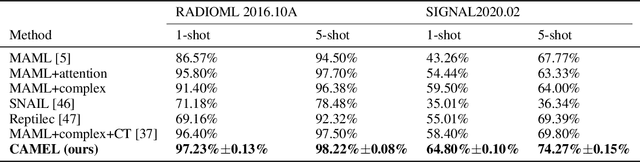
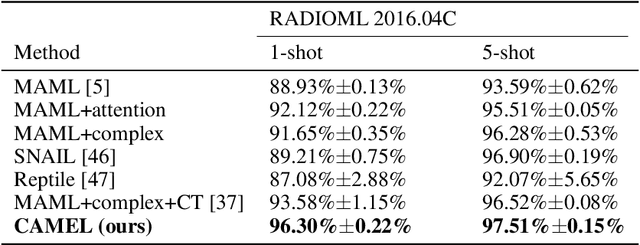
Vision transformers (ViTs) have recently been used for visual matching beyond object detection and segmentation. However, the original grid dividing strategy of ViTs neglects the spatial information of the keypoints, limiting the sensitivity to local information. Therefore, we propose \textbf{QueryTrans} (Query Transformer), which adopts a cross-attention module and keypoints-based center crop strategy for better spatial information extraction. We further integrate the graph attention module and devise a transformer-based graph matching approach \textbf{GMTR} (Graph Matching TRansformers) whereby the combinatorial nature of GM is addressed by a graph transformer neural GM solver. On standard GM benchmarks, GMTR shows competitive performance against the SOTA frameworks. Specifically, on Pascal VOC, GMTR achieves $\mathbf{83.6\%}$ accuracy, $\mathbf{0.9\%}$ higher than the SOTA framework. On Spair-71k, GMTR shows great potential and outperforms most of the previous works. Meanwhile, on Pascal VOC, QueryTrans improves the accuracy of NGMv2 from $80.1\%$ to $\mathbf{83.3\%}$, and BBGM from $79.0\%$ to $\mathbf{84.5\%}$. On Spair-71k, QueryTrans improves NGMv2 from $80.6\%$ to $\mathbf{82.5\%}$, and BBGM from $82.1\%$ to $\mathbf{83.9\%}$. Source code will be made publicly available.

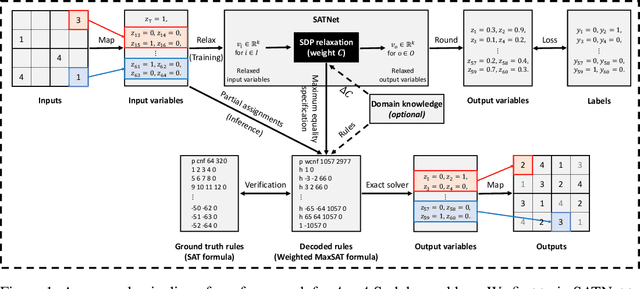
Learning Reliable Logical Rules with SATNet

Bridging logical reasoning and deep learning is crucial for advanced AI systems. In this work, we present a new framework that addresses this goal by generating interpretable and verifiable logical rules through differentiable learning, without relying on pre-specified logical structures. Our approach builds upon SATNet, a differentiable MaxSAT solver that learns the underlying rules from input-output examples. Despite its efficacy, the learned weights in SATNet are not straightforwardly interpretable, failing to produce human-readable rules. To address this, we propose a novel specification method called "maximum equality", which enables the interchangeability between the learned weights of SATNet and a set of propositional logical rules in weighted MaxSAT form. With the decoded weighted MaxSAT formula, we further introduce several effective verification techniques to validate it against the ground truth rules. Experiments on stream transformations and Sudoku problems show that our decoded rules are highly reliable: using exact solvers on them could achieve 100% accuracy, whereas the original SATNet fails to give correct solutions in many cases. Furthermore, we formally verify that our decoded logical rules are functionally equivalent to the ground truth ones.

G4SATBench: Benchmarking and Advancing SAT Solving with Graph Neural Networks

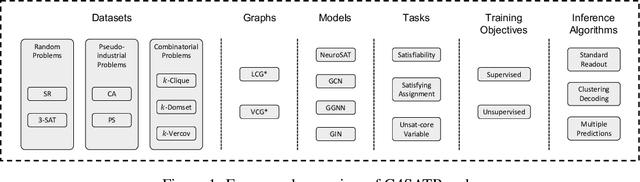
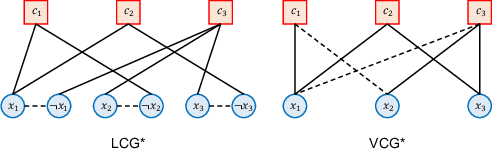
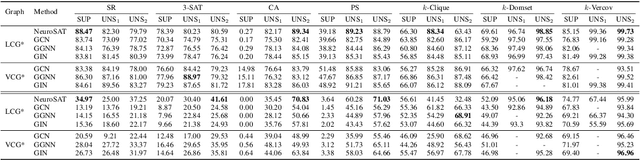
Graph neural networks (GNNs) have recently emerged as a promising approach for solving the Boolean Satisfiability Problem (SAT), offering potential alternatives to traditional backtracking or local search SAT solvers. However, despite the growing volume of literature in this field, there remains a notable absence of a unified dataset and a fair benchmark to evaluate and compare existing approaches. To address this crucial gap, we present G4SATBench, the first benchmark study that establishes a comprehensive evaluation framework for GNN-based SAT solvers. In G4SATBench, we meticulously curate a large and diverse set of SAT datasets comprising 7 problems with 3 difficulty levels and benchmark a broad range of GNN models across various prediction tasks, training objectives, and inference algorithms. To explore the learning abilities and comprehend the strengths and limitations of GNN-based SAT solvers, we also compare their solving processes with the heuristics in search-based SAT solvers. Our empirical results provide valuable insights into the performance of GNN-based SAT solvers and further suggest that existing GNN models can effectively learn a solving strategy akin to greedy local search but struggle to learn backtracking search in the latent space.