On the Efficiency of ERM in Feature Learning

Given a collection of feature maps indexed by a set $\mathcal{T}$, we study the performance of empirical risk minimization (ERM) on regression problems with square loss over the union of the linear classes induced by these feature maps. This setup aims at capturing the simplest instance of feature learning, where the model is expected to jointly learn from the data an appropriate feature map and a linear predictor. We start by studying the asymptotic quantiles of the excess risk of sequences of empirical risk minimizers. Remarkably, we show that when the set $\mathcal{T}$ is not too large and when there is a unique optimal feature map, these quantiles coincide, up to a factor of two, with those of the excess risk of the oracle procedure, which knows a priori this optimal feature map and deterministically outputs an empirical risk minimizer from the associated optimal linear class. We complement this asymptotic result with a non-asymptotic analysis that quantifies the decaying effect of the global complexity of the set $\mathcal{T}$ on the excess risk of ERM, and relates it to the size of the sublevel sets of the suboptimality of the feature maps. As an application of our results, we obtain new guarantees on the performance of the best subset selection procedure in sparse linear regression under general assumptions.

Minimax Linear Regression under the Quantile Risk

We study the problem of designing minimax procedures in linear regression under the quantile risk. We start by considering the realizable setting with independent Gaussian noise, where for any given noise level and distribution of inputs, we obtain the exact minimax quantile risk for a rich family of error functions and establish the minimaxity of OLS. This improves on the known lower bounds for the special case of square error, and provides us with a lower bound on the minimax quantile risk over larger sets of distributions. Under the square error and a fourth moment assumption on the distribution of inputs, we show that this lower bound is tight over a larger class of problems. Specifically, we prove a matching upper bound on the worst-case quantile risk of a variant of the recently proposed min-max regression procedure, thereby establishing its minimaxity, up to absolute constants. We illustrate the usefulness of our approach by extending this result to all $p$-th power error functions for $p \in (2, \infty)$. Along the way, we develop a generic analogue to the classical Bayesian method for lower bounding the minimax risk when working with the quantile risk, as well as a tight characterization of the quantiles of the smallest eigenvalue of the sample covariance matrix.

Optimal Excess Risk Bounds for Empirical Risk Minimization on $p$-norm Linear Regression

We study the performance of empirical risk minimization on the $p$-norm linear regression problem for $p \in (1, \infty)$. We show that, in the realizable case, under no moment assumptions, and up to a distribution-dependent constant, $O(d)$ samples are enough to exactly recover the target. Otherwise, for $p \in [2, \infty)$, and under weak moment assumptions on the target and the covariates, we prove a high probability excess risk bound on the empirical risk minimizer whose leading term matches, up to a constant that depends only on $p$, the asymptotically exact rate. We extend this result to the case $p \in (1, 2)$ under mild assumptions that guarantee the existence of the Hessian of the risk at its minimizer.

Contrastive Learning Can Find An Optimal Basis For Approximately View-Invariant Functions

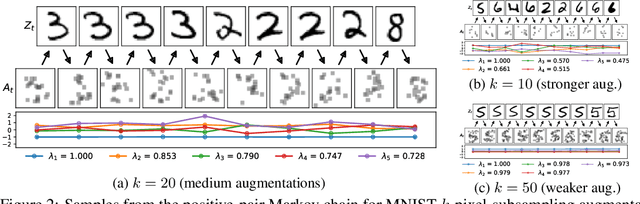
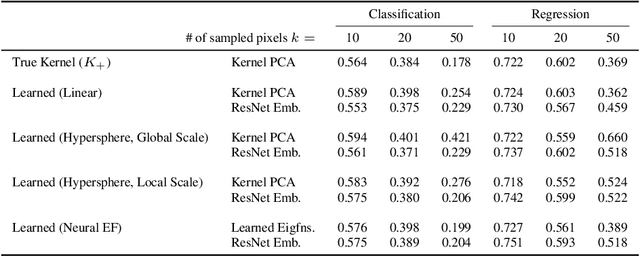
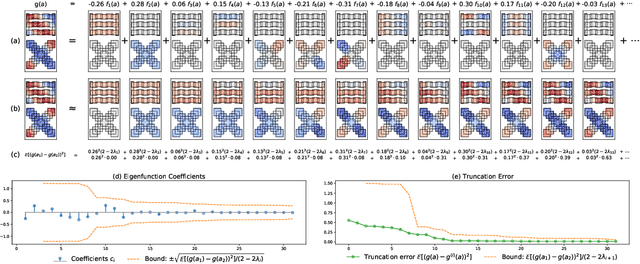
Contrastive learning is a powerful framework for learning self-supervised representations that generalize well to downstream supervised tasks. We show that multiple existing contrastive learning methods can be reinterpreted as learning kernel functions that approximate a fixed positive-pair kernel. We then prove that a simple representation obtained by combining this kernel with PCA provably minimizes the worst-case approximation error of linear predictors, under a straightforward assumption that positive pairs have similar labels. Our analysis is based on a decomposition of the target function in terms of the eigenfunctions of a positive-pair Markov chain, and a surprising equivalence between these eigenfunctions and the output of Kernel PCA. We give generalization bounds for downstream linear prediction using our Kernel PCA representation, and show empirically on a set of synthetic tasks that applying Kernel PCA to contrastive learning models can indeed approximately recover the Markov chain eigenfunctions, although the accuracy depends on the kernel parameterization as well as on the augmentation strength.

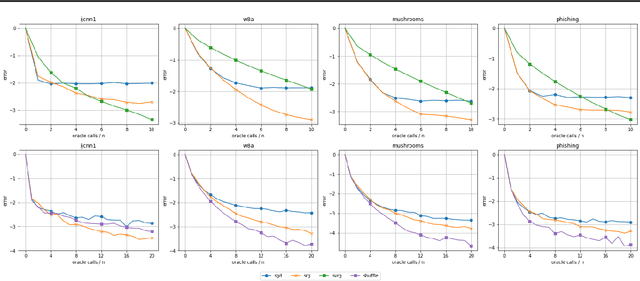
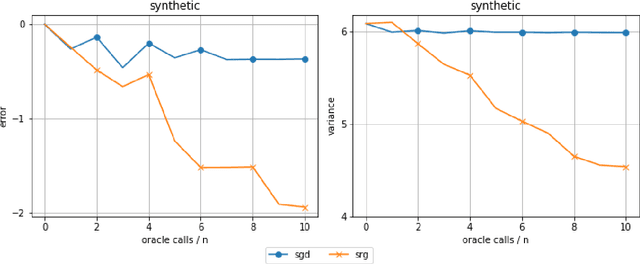
Stochastic Reweighted Gradient Descent

Despite the strong theoretical guarantees that variance-reduced finite-sum optimization algorithms enjoy, their applicability remains limited to cases where the memory overhead they introduce (SAG/SAGA), or the periodic full gradient computation they require (SVRG/SARAH) are manageable. A promising approach to achieving variance reduction while avoiding these drawbacks is the use of importance sampling instead of control variates. While many such methods have been proposed in the literature, directly proving that they improve the convergence of the resulting optimization algorithm has remained elusive. In this work, we propose an importance-sampling-based algorithm we call SRG (stochastic reweighted gradient). We analyze the convergence of SRG in the strongly-convex case and show that, while it does not recover the linear rate of control variates methods, it provably outperforms SGD. We pay particular attention to the time and memory overhead of our proposed method, and design a specialized red-black tree allowing its efficient implementation. Finally, we present empirical results to support our findings.

Adaptive Importance Sampling for Finite-Sum Optimization and Sampling with Decreasing Step-Sizes

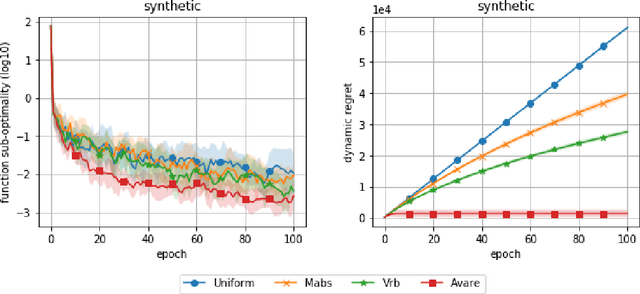
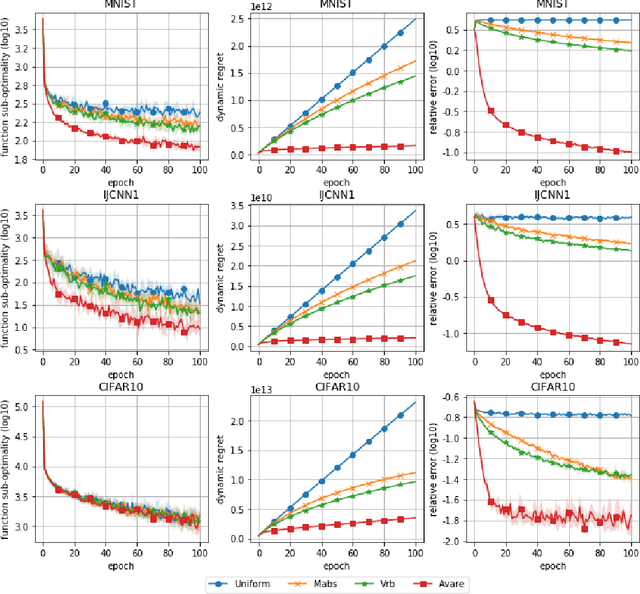
Reducing the variance of the gradient estimator is known to improve the convergence rate of stochastic gradient-based optimization and sampling algorithms. One way of achieving variance reduction is to design importance sampling strategies. Recently, the problem of designing such schemes was formulated as an online learning problem with bandit feedback, and algorithms with sub-linear static regret were designed. In this work, we build on this framework and propose Avare, a simple and efficient algorithm for adaptive importance sampling for finite-sum optimization and sampling with decreasing step-sizes. Under standard technical conditions, we show that Avare achieves $\mathcal{O}(T^{2/3})$ and $\mathcal{O}(T^{5/6})$ dynamic regret for SGD and SGLD respectively when run with $\mathcal{O}(1/t)$ step sizes. We achieve this dynamic regret bound by leveraging our knowledge of the dynamics defined by the algorithm, and combining ideas from online learning and variance-reduced stochastic optimization. We validate empirically the performance of our algorithm and identify settings in which it leads to significant improvements.