Accelerating Generalized Random Forests with Fixed-Point Trees

Generalized random forests arXiv:1610.01271 build upon the well-established success of conventional forests (Breiman, 2001) to offer a flexible and powerful non-parametric method for estimating local solutions of heterogeneous estimating equations. Estimators are constructed by leveraging random forests as an adaptive kernel weighting algorithm and implemented through a gradient-based tree-growing procedure. By expressing this gradient-based approximation as being induced from a single Newton-Raphson root-finding iteration, and drawing upon the connection between estimating equations and fixed-point problems arXiv:2110.11074, we propose a new tree-growing rule for generalized random forests induced from a fixed-point iteration type of approximation, enabling gradient-free optimization, and yielding substantial time savings for tasks involving even modest dimensionality of the target quantity (e.g. multiple/multi-level treatment effects). We develop an asymptotic theory for estimators obtained from forests whose trees are grown through the fixed-point splitting rule, and provide numerical simulations demonstrating that the estimators obtained from such forests are comparable to those obtained from the more costly gradient-based rule.

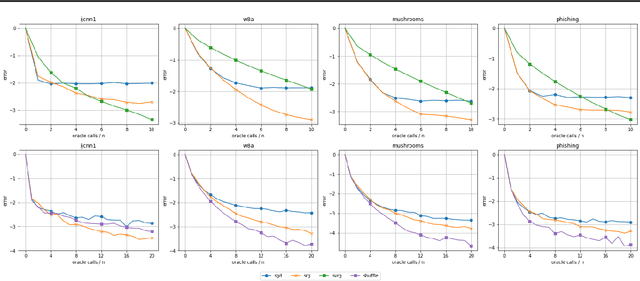
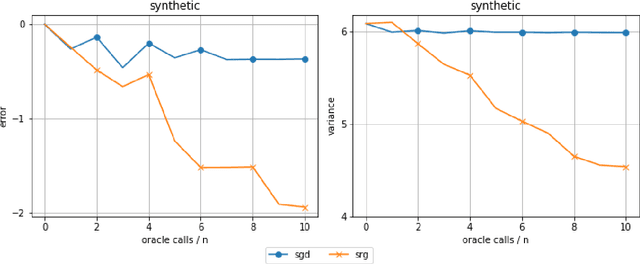
Stochastic Reweighted Gradient Descent

Despite the strong theoretical guarantees that variance-reduced finite-sum optimization algorithms enjoy, their applicability remains limited to cases where the memory overhead they introduce (SAG/SAGA), or the periodic full gradient computation they require (SVRG/SARAH) are manageable. A promising approach to achieving variance reduction while avoiding these drawbacks is the use of importance sampling instead of control variates. While many such methods have been proposed in the literature, directly proving that they improve the convergence of the resulting optimization algorithm has remained elusive. In this work, we propose an importance-sampling-based algorithm we call SRG (stochastic reweighted gradient). We analyze the convergence of SRG in the strongly-convex case and show that, while it does not recover the linear rate of control variates methods, it provably outperforms SGD. We pay particular attention to the time and memory overhead of our proposed method, and design a specialized red-black tree allowing its efficient implementation. Finally, we present empirical results to support our findings.

Adaptive Importance Sampling for Finite-Sum Optimization and Sampling with Decreasing Step-Sizes

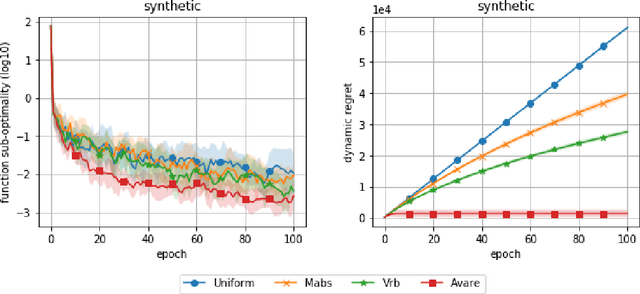
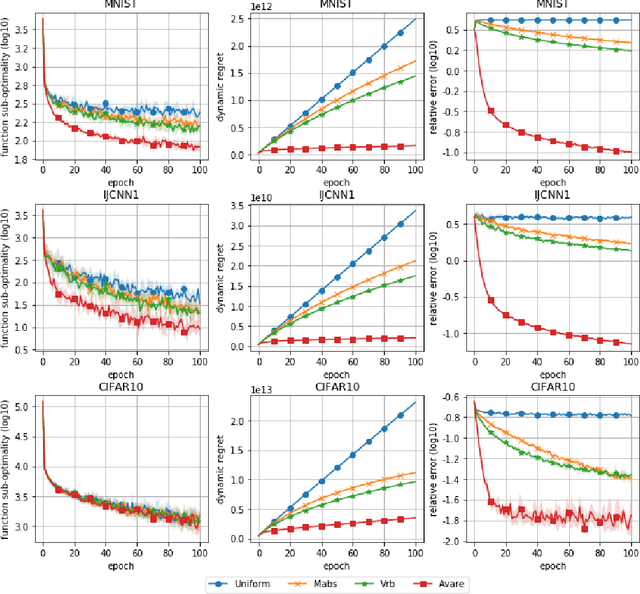
Reducing the variance of the gradient estimator is known to improve the convergence rate of stochastic gradient-based optimization and sampling algorithms. One way of achieving variance reduction is to design importance sampling strategies. Recently, the problem of designing such schemes was formulated as an online learning problem with bandit feedback, and algorithms with sub-linear static regret were designed. In this work, we build on this framework and propose Avare, a simple and efficient algorithm for adaptive importance sampling for finite-sum optimization and sampling with decreasing step-sizes. Under standard technical conditions, we show that Avare achieves $\mathcal{O}(T^{2/3})$ and $\mathcal{O}(T^{5/6})$ dynamic regret for SGD and SGLD respectively when run with $\mathcal{O}(1/t)$ step sizes. We achieve this dynamic regret bound by leveraging our knowledge of the dynamics defined by the algorithm, and combining ideas from online learning and variance-reduced stochastic optimization. We validate empirically the performance of our algorithm and identify settings in which it leads to significant improvements.