On the Efficiency of ERM in Feature Learning

Given a collection of feature maps indexed by a set $\mathcal{T}$, we study the performance of empirical risk minimization (ERM) on regression problems with square loss over the union of the linear classes induced by these feature maps. This setup aims at capturing the simplest instance of feature learning, where the model is expected to jointly learn from the data an appropriate feature map and a linear predictor. We start by studying the asymptotic quantiles of the excess risk of sequences of empirical risk minimizers. Remarkably, we show that when the set $\mathcal{T}$ is not too large and when there is a unique optimal feature map, these quantiles coincide, up to a factor of two, with those of the excess risk of the oracle procedure, which knows a priori this optimal feature map and deterministically outputs an empirical risk minimizer from the associated optimal linear class. We complement this asymptotic result with a non-asymptotic analysis that quantifies the decaying effect of the global complexity of the set $\mathcal{T}$ on the excess risk of ERM, and relates it to the size of the sublevel sets of the suboptimality of the feature maps. As an application of our results, we obtain new guarantees on the performance of the best subset selection procedure in sparse linear regression under general assumptions.

Robust Feature Learning for Multi-Index Models in High Dimensions

Recently, there have been numerous studies on feature learning with neural networks, specifically on learning single- and multi-index models where the target is a function of a low-dimensional projection of the input. Prior works have shown that in high dimensions, the majority of the compute and data resources are spent on recovering the low-dimensional projection; once this subspace is recovered, the remainder of the target can be learned independently of the ambient dimension. However, implications of feature learning in adversarial settings remain unexplored. In this work, we take the first steps towards understanding adversarially robust feature learning with neural networks. Specifically, we prove that the hidden directions of a multi-index model offer a Bayes optimal low-dimensional projection for robustness against $\ell_2$-bounded adversarial perturbations under the squared loss, assuming that the multi-index coordinates are statistically independent from the rest of the coordinates. Therefore, robust learning can be achieved by first performing standard feature learning, then robustly tuning a linear readout layer on top of the standard representations. In particular, we show that adversarially robust learning is just as easy as standard learning, in the sense that the additional number of samples needed to robustly learn multi-index models when compared to standard learning, does not depend on dimensionality.

Learning Multi-Index Models with Neural Networks via Mean-Field Langevin Dynamics

We study the problem of learning multi-index models in high-dimensions using a two-layer neural network trained with the mean-field Langevin algorithm. Under mild distributional assumptions on the data, we characterize the effective dimension $d_{\mathrm{eff}}$ that controls both sample and computational complexity by utilizing the adaptivity of neural networks to latent low-dimensional structures. When the data exhibit such a structure, $d_{\mathrm{eff}}$ can be significantly smaller than the ambient dimension. We prove that the sample complexity grows almost linearly with $d_{\mathrm{eff}}$, bypassing the limitations of the information and generative exponents that appeared in recent analyses of gradient-based feature learning. On the other hand, the computational complexity may inevitably grow exponentially with $d_{\mathrm{eff}}$ in the worst-case scenario. Motivated by improving computational complexity, we take the first steps towards polynomial time convergence of the mean-field Langevin algorithm by investigating a setting where the weights are constrained to be on a compact manifold with positive Ricci curvature, such as the hypersphere. There, we study assumptions under which polynomial time convergence is achievable, whereas similar assumptions in the Euclidean setting lead to exponential time complexity.

Minimax Linear Regression under the Quantile Risk

We study the problem of designing minimax procedures in linear regression under the quantile risk. We start by considering the realizable setting with independent Gaussian noise, where for any given noise level and distribution of inputs, we obtain the exact minimax quantile risk for a rich family of error functions and establish the minimaxity of OLS. This improves on the known lower bounds for the special case of square error, and provides us with a lower bound on the minimax quantile risk over larger sets of distributions. Under the square error and a fourth moment assumption on the distribution of inputs, we show that this lower bound is tight over a larger class of problems. Specifically, we prove a matching upper bound on the worst-case quantile risk of a variant of the recently proposed min-max regression procedure, thereby establishing its minimaxity, up to absolute constants. We illustrate the usefulness of our approach by extending this result to all $p$-th power error functions for $p \in (2, \infty)$. Along the way, we develop a generic analogue to the classical Bayesian method for lower bounding the minimax risk when working with the quantile risk, as well as a tight characterization of the quantiles of the smallest eigenvalue of the sample covariance matrix.

Pruning is Optimal for Learning Sparse Features in High-Dimensions

While it is commonly observed in practice that pruning networks to a certain level of sparsity can improve the quality of the features, a theoretical explanation of this phenomenon remains elusive. In this work, we investigate this by demonstrating that a broad class of statistical models can be optimally learned using pruned neural networks trained with gradient descent, in high-dimensions. We consider learning both single-index and multi-index models of the form $y = \sigma^*(\boldsymbol{V}^{\top} \boldsymbol{x}) + \epsilon$, where $\sigma^*$ is a degree-$p$ polynomial, and $\boldsymbol{V} \in \mathbbm{R}^{d \times r}$ with $r \ll d$, is the matrix containing relevant model directions. We assume that $\boldsymbol{V}$ satisfies a certain $\ell_q$-sparsity condition for matrices and show that pruning neural networks proportional to the sparsity level of $\boldsymbol{V}$ improves their sample complexity compared to unpruned networks. Furthermore, we establish Correlational Statistical Query (CSQ) lower bounds in this setting, which take the sparsity level of $\boldsymbol{V}$ into account. We show that if the sparsity level of $\boldsymbol{V}$ exceeds a certain threshold, training pruned networks with a gradient descent algorithm achieves the sample complexity suggested by the CSQ lower bound. In the same scenario, however, our results imply that basis-independent methods such as models trained via standard gradient descent initialized with rotationally invariant random weights can provably achieve only suboptimal sample complexity.

A Separation in Heavy-Tailed Sampling: Gaussian vs. Stable Oracles for Proximal Samplers

We study the complexity of heavy-tailed sampling and present a separation result in terms of obtaining high-accuracy versus low-accuracy guarantees i.e., samplers that require only $O(\log(1/\varepsilon))$ versus $\Omega(\text{poly}(1/\varepsilon))$ iterations to output a sample which is $\varepsilon$-close to the target in $\chi^2$-divergence. Our results are presented for proximal samplers that are based on Gaussian versus stable oracles. We show that proximal samplers based on the Gaussian oracle have a fundamental barrier in that they necessarily achieve only low-accuracy guarantees when sampling from a class of heavy-tailed targets. In contrast, proximal samplers based on the stable oracle exhibit high-accuracy guarantees, thereby overcoming the aforementioned limitation. We also prove lower bounds for samplers under the stable oracle and show that our upper bounds cannot be fundamentally improved.

Sampling from the Mean-Field Stationary Distribution

We study the complexity of sampling from the stationary distribution of a mean-field SDE, or equivalently, the complexity of minimizing a functional over the space of probability measures which includes an interaction term. Our main insight is to decouple the two key aspects of this problem: (1) approximation of the mean-field SDE via a finite-particle system, via uniform-in-time propagation of chaos, and (2) sampling from the finite-particle stationary distribution, via standard log-concave samplers. Our approach is conceptually simpler and its flexibility allows for incorporating the state-of-the-art for both algorithms and theory. This leads to improved guarantees in numerous settings, including better guarantees for optimizing certain two-layer neural networks in the mean-field regime.

Optimal Excess Risk Bounds for Empirical Risk Minimization on $p$-norm Linear Regression

We study the performance of empirical risk minimization on the $p$-norm linear regression problem for $p \in (1, \infty)$. We show that, in the realizable case, under no moment assumptions, and up to a distribution-dependent constant, $O(d)$ samples are enough to exactly recover the target. Otherwise, for $p \in [2, \infty)$, and under weak moment assumptions on the target and the covariates, we prove a high probability excess risk bound on the empirical risk minimizer whose leading term matches, up to a constant that depends only on $p$, the asymptotically exact rate. We extend this result to the case $p \in (1, 2)$ under mild assumptions that guarantee the existence of the Hessian of the risk at its minimizer.

Beyond Labeling Oracles: What does it mean to steal ML models?

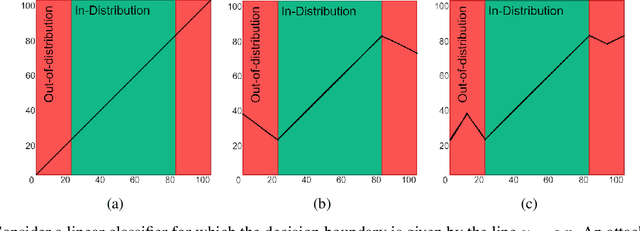
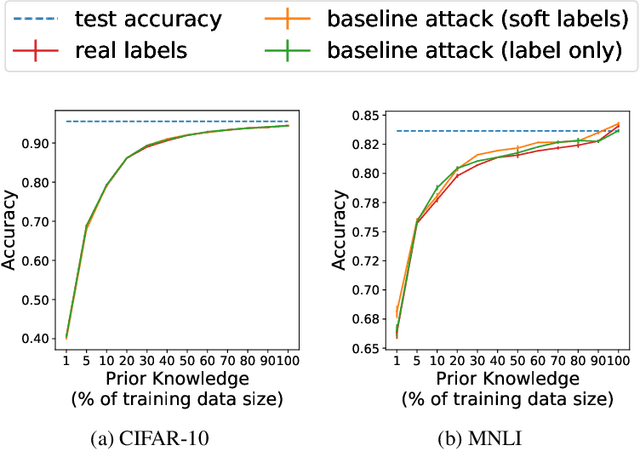
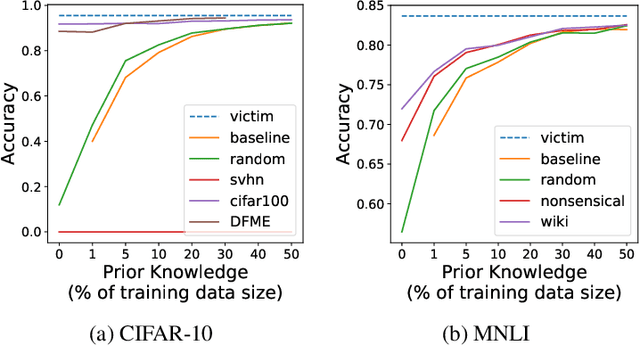
Model extraction attacks are designed to steal trained models with only query access, as is often provided through APIs that ML-as-a-Service providers offer. ML models are expensive to train, in part because data is hard to obtain, and a primary incentive for model extraction is to acquire a model while incurring less cost than training from scratch. Literature on model extraction commonly claims or presumes that the attacker is able to save on both data acquisition and labeling costs. We show that the attacker often does not. This is because current attacks implicitly rely on the adversary being able to sample from the victim model's data distribution. We thoroughly evaluate factors influencing the success of model extraction. We discover that prior knowledge of the attacker, i.e. access to in-distribution data, dominates other factors like the attack policy the adversary follows to choose which queries to make to the victim model API. Thus, an adversary looking to develop an equally capable model with a fixed budget has little practical incentive to perform model extraction, since for the attack to work they need to collect in-distribution data, saving only on the cost of labeling. With low labeling costs in the current market, the usefulness of such attacks is questionable. Ultimately, we demonstrate that the effect of prior knowledge needs to be explicitly decoupled from the attack policy. To this end, we propose a benchmark to evaluate attack policy directly.

Gradient-Based Feature Learning under Structured Data

Recent works have demonstrated that the sample complexity of gradient-based learning of single index models, i.e. functions that depend on a 1-dimensional projection of the input data, is governed by their information exponent. However, these results are only concerned with isotropic data, while in practice the input often contains additional structure which can implicitly guide the algorithm. In this work, we investigate the effect of a spiked covariance structure and reveal several interesting phenomena. First, we show that in the anisotropic setting, the commonly used spherical gradient dynamics may fail to recover the true direction, even when the spike is perfectly aligned with the target direction. Next, we show that appropriate weight normalization that is reminiscent of batch normalization can alleviate this issue. Further, by exploiting the alignment between the (spiked) input covariance and the target, we obtain improved sample complexity compared to the isotropic case. In particular, under the spiked model with a suitably large spike, the sample complexity of gradient-based training can be made independent of the information exponent while also outperforming lower bounds for rotationally invariant kernel methods.