Rod Flow: A Continuous-Time Model for Gradient Descent at the Edge of Stability

How can we understand gradient-based training over non-convex landscapes? The edge of stability phenomenon, introduced in Cohen et al. (2021), indicates that the answer is not so simple: namely, gradient descent (GD) with large step sizes often diverges away from the gradient flow. In this regime, the "Central Flow", recently proposed in Cohen et al. (2025), provides an accurate ODE approximation to the GD dynamics over many architectures. In this work, we propose Rod Flow, an alternative ODE approximation, which carries the following advantages: (1) it rests on a principled derivation stemming from a physical picture of GD iterates as an extended one-dimensional object -- a "rod"; (2) it better captures GD dynamics for simple toy examples and matches the accuracy of Central Flow for representative neural network architectures, and (3) is explicit and cheap to compute. Theoretically, we prove that Rod Flow correctly predicts the critical sharpness threshold and explains self-stabilization in quartic potentials. We validate our theory with a range of numerical experiments.

High-accuracy sampling for diffusion models and log-concave distributions

We present algorithms for diffusion model sampling which obtain $δ$-error in $\mathrm{polylog}(1/δ)$ steps, given access to $\widetilde O(δ)$-accurate score estimates in $L^2$. This is an exponential improvement over all previous results. Specifically, under minimal data assumptions, the complexity is $\widetilde O(d\,\mathrm{polylog}(1/δ))$ where $d$ is the dimension of the data; under a non-uniform $L$-Lipschitz condition, the complexity is $\widetilde O(\sqrt{dL}\,\mathrm{polylog}(1/δ))$; and if the data distribution has intrinsic dimension $d_\star$, then the complexity reduces to $\widetilde O(d_\star\,\mathrm{polylog}(1/δ))$. Our approach also yields the first $\mathrm{polylog}(1/δ)$ complexity sampler for general log-concave distributions using only gradient evaluations.

Theory and computation for structured variational inference

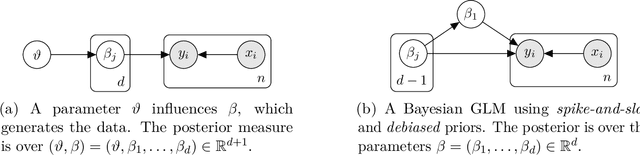
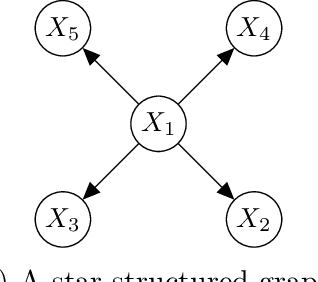
Structured variational inference constitutes a core methodology in modern statistical applications. Unlike mean-field variational inference, the approximate posterior is assumed to have interdependent structure. We consider the natural setting of star-structured variational inference, where a root variable impacts all the other ones. We prove the first results for existence, uniqueness, and self-consistency of the variational approximation. In turn, we derive quantitative approximation error bounds for the variational approximation to the posterior, extending prior work from the mean-field setting to the star-structured setting. We also develop a gradient-based algorithm with provable guarantees for computing the variational approximation using ideas from optimal transport theory. We explore the implications of our results for Gaussian measures and hierarchical Bayesian models, including generalized linear models with location family priors and spike-and-slab priors with one-dimensional debiasing. As a by-product of our analysis, we develop new stability results for star-separable transport maps which might be of independent interest.

Sublinear iterations can suffice even for DDPMs

SDE-based methods such as denoising diffusion probabilistic models (DDPMs) have shown remarkable success in real-world sample generation tasks. Prior analyses of DDPMs have been focused on the exponential Euler discretization, showing guarantees that generally depend at least linearly on the dimension or initial Fisher information. Inspired by works in log-concave sampling (Shen and Lee, 2019), we analyze an integrator -- the denoising diffusion randomized midpoint method (DDRaM) -- that leverages an additional randomized midpoint to better approximate the SDE. Using a recently-developed analytic framework called the "shifted composition rule", we show that this algorithm enjoys favorable discretization properties under appropriate smoothness assumptions, with sublinear $\widetilde{O}(\sqrt{d})$ score evaluations needed to ensure convergence. This is the first sublinear complexity bound for pure DDPM sampling -- prior works which obtained such bounds worked instead with ODE-based sampling and had to make modifications to the sampler which deviate from how they are used in practice. We also provide experimental validation of the advantages of our method, showing that it performs well in practice with pre-trained image synthesis models.

Gaussian mixture layers for neural networks

The mean-field theory for two-layer neural networks considers infinitely wide networks that are linearly parameterized by a probability measure over the parameter space. This nonparametric perspective has significantly advanced both the theoretical and conceptual understanding of neural networks, with substantial efforts made to validate its applicability to networks of moderate width. In this work, we explore the opposite direction, investigating whether dynamics can be directly implemented over probability measures. Specifically, we employ Gaussian mixture models as a flexible and expressive parametric family of distributions together with the theory of Wasserstein gradient flows to derive training dynamics for such measures. Our approach introduces a new type of layer -- the Gaussian mixture (GM) layer -- that can be integrated into neural network architectures. As a proof of concept, we validate our proposal through experiments on simple classification tasks, where a GM layer achieves test performance comparable to that of a two-layer fully connected network. Furthermore, we examine the behavior of these dynamics and demonstrate numerically that GM layers exhibit markedly different behavior compared to classical fully connected layers, even when the latter are large enough to be considered in the mean-field regime.

DDPM Score Matching and Distribution Learning

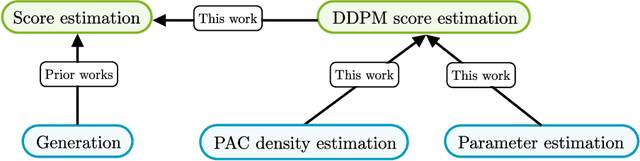
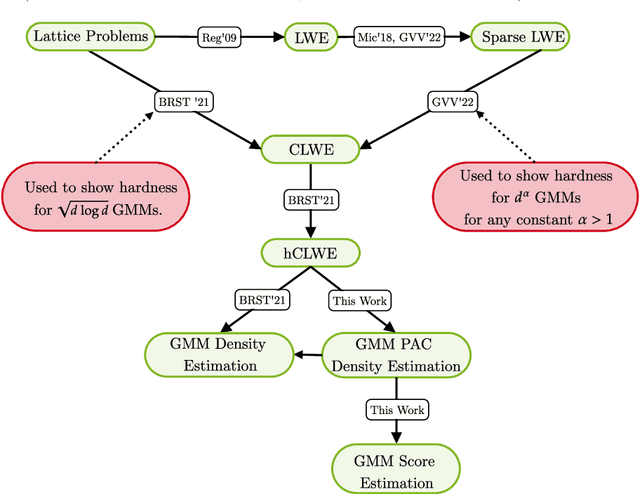
Score estimation is the backbone of score-based generative models (SGMs), especially denoising diffusion probabilistic models (DDPMs). A key result in this area shows that with accurate score estimates, SGMs can efficiently generate samples from any realistic data distribution (Chen et al., ICLR'23; Lee et al., ALT'23). This distribution learning result, where the learned distribution is implicitly that of the sampler's output, does not explain how score estimation relates to classical tasks of parameter and density estimation. This paper introduces a framework that reduces score estimation to these two tasks, with various implications for statistical and computational learning theory: Parameter Estimation: Koehler et al. (ICLR'23) demonstrate that a score-matching variant is statistically inefficient for the parametric estimation of multimodal densities common in practice. In contrast, we show that under mild conditions, denoising score-matching in DDPMs is asymptotically efficient. Density Estimation: By linking generation to score estimation, we lift existing score estimation guarantees to $(\epsilon,\delta)$-PAC density estimation, i.e., a function approximating the target log-density within $\epsilon$ on all but a $\delta$-fraction of the space. We provide (i) minimax rates for density estimation over H\"older classes and (ii) a quasi-polynomial PAC density estimation algorithm for the classical Gaussian location mixture model, building on and addressing an open problem from Gatmiry et al. (arXiv'24). Lower Bounds for Score Estimation: Our framework offers the first principled method to prove computational lower bounds for score estimation across general distributions. As an application, we establish cryptographic lower bounds for score estimation in general Gaussian mixture models, conceptually recovering Song's (NeurIPS'24) result and advancing his key open problem.

Shifted Composition III: Local Error Framework for KL Divergence

Coupling arguments are a central tool for bounding the deviation between two stochastic processes, but traditionally have been limited to Wasserstein metrics. In this paper, we apply the shifted composition rule--an information-theoretic principle introduced in our earlier work--in order to adapt coupling arguments to the Kullback-Leibler (KL) divergence. Our framework combine the strengths of two previously disparate approaches: local error analysis and Girsanov's theorem. Akin to the former, it yields tight bounds by incorporating the so-called weak error, and is user-friendly in that it only requires easily verified local assumptions; and akin to the latter, it yields KL divergence guarantees and applies beyond Wasserstein contractivity. We apply this framework to the problem of sampling from a target distribution $\pi$. Here, the two stochastic processes are the Langevin diffusion and an algorithmic discretization thereof. Our framework provides a unified analysis when $\pi$ is assumed to be strongly log-concave (SLC), weakly log-concave (WLC), or to satisfy a log-Sobolev inequality (LSI). Among other results, this yields KL guarantees for the randomized midpoint discretization of the Langevin diffusion. Notably, our result: (1) yields the optimal $\tilde O(\sqrt d/\epsilon)$ rate in the SLC and LSI settings; (2) is the first result to hold beyond the 2-Wasserstein metric in the SLC setting; and (3) is the first result to hold in \emph{any} metric in the WLC and LSI settings.

Statistical optimal transport

We present an introduction to the field of statistical optimal transport, based on lectures given at \'Ecole d'\'Et\'e de Probabilit\'es de Saint-Flour XLIX.

Sampling from the Mean-Field Stationary Distribution

We study the complexity of sampling from the stationary distribution of a mean-field SDE, or equivalently, the complexity of minimizing a functional over the space of probability measures which includes an interaction term. Our main insight is to decouple the two key aspects of this problem: (1) approximation of the mean-field SDE via a finite-particle system, via uniform-in-time propagation of chaos, and (2) sampling from the finite-particle stationary distribution, via standard log-concave samplers. Our approach is conceptually simpler and its flexibility allows for incorporating the state-of-the-art for both algorithms and theory. This leads to improved guarantees in numerous settings, including better guarantees for optimizing certain two-layer neural networks in the mean-field regime.

Fast parallel sampling under isoperimetry

We show how to sample in parallel from a distribution $\pi$ over $\mathbb R^d$ that satisfies a log-Sobolev inequality and has a smooth log-density, by parallelizing the Langevin (resp. underdamped Langevin) algorithms. We show that our algorithm outputs samples from a distribution $\hat\pi$ that is close to $\pi$ in Kullback--Leibler (KL) divergence (resp. total variation (TV) distance), while using only $\log(d)^{O(1)}$ parallel rounds and $\widetilde{O}(d)$ (resp. $\widetilde O(\sqrt d)$) gradient evaluations in total. This constitutes the first parallel sampling algorithms with TV distance guarantees. For our main application, we show how to combine the TV distance guarantees of our algorithms with prior works and obtain RNC sampling-to-counting reductions for families of discrete distribution on the hypercube $\{\pm 1\}^n$ that are closed under exponential tilts and have bounded covariance. Consequently, we obtain an RNC sampler for directed Eulerian tours and asymmetric determinantal point processes, resolving open questions raised in prior works.