Mean Estimation from Coarse Data: Characterizations and Efficient Algorithms

Coarse data arise when learners observe only partial information about samples; namely, a set containing the sample rather than its exact value. This occurs naturally through measurement rounding, sensor limitations, and lag in economic systems. We study Gaussian mean estimation from coarse data, where each true sample $x$ is drawn from a $d$-dimensional Gaussian distribution with identity covariance, but is revealed only through the set of a partition containing $x$. When the coarse samples, roughly speaking, have ``low'' information, the mean cannot be uniquely recovered from observed samples (i.e., the problem is not identifiable). Recent work by Fotakis, Kalavasis, Kontonis, and Tzamos [FKKT21] established that sample-efficient mean estimation is possible when the unknown mean is identifiable and the partition consists of only convex sets. Moreover, they showed that without convexity, mean estimation becomes NP-hard. However, two fundamental questions remained open: (1) When is the mean identifiable under convex partitions? (2) Is computationally efficient estimation possible under identifiability and convex partitions? This work resolves both questions. [...]

Linear Regression with Unknown Truncation Beyond Gaussian Features

In truncated linear regression, samples $(x,y)$ are shown only when the outcome $y$ falls inside a certain survival set $S^\star$ and the goal is to estimate the unknown $d$-dimensional regressor $w^\star$. This problem has a long history of study in Statistics and Machine Learning going back to the works of (Galton, 1897; Tobin, 1958) and more recently in, e.g., (Daskalakis et al., 2019; 2021; Lee et al., 2023; 2024). Despite this long history, however, most prior works are limited to the special case where $S^\star$ is precisely known. The more practically relevant case, where $S^\star$ is unknown and must be learned from data, remains open: indeed, here the only available algorithms require strong assumptions on the distribution of the feature vectors (e.g., Gaussianity) and, even then, have a $d^{\mathrm{poly} (1/\varepsilon)}$ run time for achieving $\varepsilon$ accuracy. In this work, we give the first algorithm for truncated linear regression with unknown survival set that runs in $\mathrm{poly} (d/\varepsilon)$ time, by only requiring that the feature vectors are sub-Gaussian. Our algorithm relies on a novel subroutine for efficiently learning unions of a bounded number of intervals using access to positive examples (without any negative examples) under a certain smoothness condition. This learning guarantee adds to the line of works on positive-only PAC learning and may be of independent interest.

Learning Mixture Models via Efficient High-dimensional Sparse Fourier Transforms

In this work, we give a ${\rm poly}(d,k)$ time and sample algorithm for efficiently learning the parameters of a mixture of $k$ spherical distributions in $d$ dimensions. Unlike all previous methods, our techniques apply to heavy-tailed distributions and include examples that do not even have finite covariances. Our method succeeds whenever the cluster distributions have a characteristic function with sufficiently heavy tails. Such distributions include the Laplace distribution but crucially exclude Gaussians. All previous methods for learning mixture models relied implicitly or explicitly on the low-degree moments. Even for the case of Laplace distributions, we prove that any such algorithm must use super-polynomially many samples. Our method thus adds to the short list of techniques that bypass the limitations of the method of moments. Somewhat surprisingly, our algorithm does not require any minimum separation between the cluster means. This is in stark contrast to spherical Gaussian mixtures where a minimum $\ell_2$-separation is provably necessary even information-theoretically [Regev and Vijayaraghavan '17]. Our methods compose well with existing techniques and allow obtaining ''best of both worlds" guarantees for mixtures where every component either has a heavy-tailed characteristic function or has a sub-Gaussian tail with a light-tailed characteristic function. Our algorithm is based on a new approach to learning mixture models via efficient high-dimensional sparse Fourier transforms. We believe that this method will find more applications to statistical estimation. As an example, we give an algorithm for consistent robust mean estimation against noise-oblivious adversaries, a model practically motivated by the literature on multiple hypothesis testing. It was formally proposed in a recent Master's thesis by one of the authors, and has already inspired follow-up works.

What Makes Treatment Effects Identifiable? Characterizations and Estimators Beyond Unconfoundedness

Most of the widely used estimators of the average treatment effect (ATE) in causal inference rely on the assumptions of unconfoundedness and overlap. Unconfoundedness requires that the observed covariates account for all correlations between the outcome and treatment. Overlap requires the existence of randomness in treatment decisions for all individuals. Nevertheless, many types of studies frequently violate unconfoundedness or overlap, for instance, observational studies with deterministic treatment decisions -- popularly known as Regression Discontinuity designs -- violate overlap. In this paper, we initiate the study of general conditions that enable the identification of the average treatment effect, extending beyond unconfoundedness and overlap. In particular, following the paradigm of statistical learning theory, we provide an interpretable condition that is sufficient and nearly necessary for the identification of ATE. Moreover, this condition characterizes the identification of the average treatment effect on the treated (ATT) and can be used to characterize other treatment effects as well. To illustrate the utility of our condition, we present several well-studied scenarios where our condition is satisfied and, hence, we prove that ATE can be identified in regimes that prior works could not capture. For example, under mild assumptions on the data distributions, this holds for the models proposed by Tan (2006) and Rosenbaum (2002), and the Regression Discontinuity design model introduced by Thistlethwaite and Campbell (1960). For each of these scenarios, we also show that, under natural additional assumptions, ATE can be estimated from finite samples. We believe these findings open new avenues for bridging learning-theoretic insights and causal inference methodologies, particularly in observational studies with complex treatment mechanisms.

DDPM Score Matching and Distribution Learning

Score estimation is the backbone of score-based generative models (SGMs), especially denoising diffusion probabilistic models (DDPMs). A key result in this area shows that with accurate score estimates, SGMs can efficiently generate samples from any realistic data distribution (Chen et al., ICLR'23; Lee et al., ALT'23). This distribution learning result, where the learned distribution is implicitly that of the sampler's output, does not explain how score estimation relates to classical tasks of parameter and density estimation. This paper introduces a framework that reduces score estimation to these two tasks, with various implications for statistical and computational learning theory: Parameter Estimation: Koehler et al. (ICLR'23) demonstrate that a score-matching variant is statistically inefficient for the parametric estimation of multimodal densities common in practice. In contrast, we show that under mild conditions, denoising score-matching in DDPMs is asymptotically efficient. Density Estimation: By linking generation to score estimation, we lift existing score estimation guarantees to $(\epsilon,\delta)$-PAC density estimation, i.e., a function approximating the target log-density within $\epsilon$ on all but a $\delta$-fraction of the space. We provide (i) minimax rates for density estimation over H\"older classes and (ii) a quasi-polynomial PAC density estimation algorithm for the classical Gaussian location mixture model, building on and addressing an open problem from Gatmiry et al. (arXiv'24). Lower Bounds for Score Estimation: Our framework offers the first principled method to prove computational lower bounds for score estimation across general distributions. As an application, we establish cryptographic lower bounds for score estimation in general Gaussian mixture models, conceptually recovering Song's (NeurIPS'24) result and advancing his key open problem.

Can SGD Select Good Fishermen? Local Convergence under Self-Selection Biases and Beyond

We revisit the problem of estimating $k$ linear regressors with self-selection bias in $d$ dimensions with the maximum selection criterion, as introduced by Cherapanamjeri, Daskalakis, Ilyas, and Zampetakis [CDIZ23, STOC'23]. Our main result is a $\operatorname{poly}(d,k,1/\varepsilon) + {k}^{O(k)}$ time algorithm for this problem, which yields an improvement in the running time of the algorithms of [CDIZ23] and [GM24, arXiv]. We achieve this by providing the first local convergence algorithm for self-selection, thus resolving the main open question of [CDIZ23]. To obtain this algorithm, we reduce self-selection to a seemingly unrelated statistical problem called coarsening. Coarsening occurs when one does not observe the exact value of the sample but only some set (a subset of the sample space) that contains the exact value. Inference from coarse samples arises in various real-world applications due to rounding by humans and algorithms, limited precision of instruments, and lag in multi-agent systems. Our reduction to coarsening is intuitive and relies on the geometry of the self-selection problem, which enables us to bypass the limitations of previous analytic approaches. To demonstrate its applicability, we provide a local convergence algorithm for linear regression under another self-selection criterion, which is related to second-price auction data. Further, we give the first polynomial time local convergence algorithm for coarse Gaussian mean estimation given samples generated from a convex partition. Previously, only a sample-efficient algorithm was known due to Fotakis, Kalavasis, Kontonis, and Tzamos [FKKT21, COLT'21].

Does Generation Require Memorization? Creative Diffusion Models using Ambient Diffusion

There is strong empirical evidence that the state-of-the-art diffusion modeling paradigm leads to models that memorize the training set, especially when the training set is small. Prior methods to mitigate the memorization problem often lead to a decrease in image quality. Is it possible to obtain strong and creative generative models, i.e., models that achieve high generation quality and low memorization? Despite the current pessimistic landscape of results, we make significant progress in pushing the trade-off between fidelity and memorization. We first provide theoretical evidence that memorization in diffusion models is only necessary for denoising problems at low noise scales (usually used in generating high-frequency details). Using this theoretical insight, we propose a simple, principled method to train the diffusion models using noisy data at large noise scales. We show that our method significantly reduces memorization without decreasing the image quality, for both text-conditional and unconditional models and for a variety of data availability settings.

Characterizations of Language Generation With Breadth

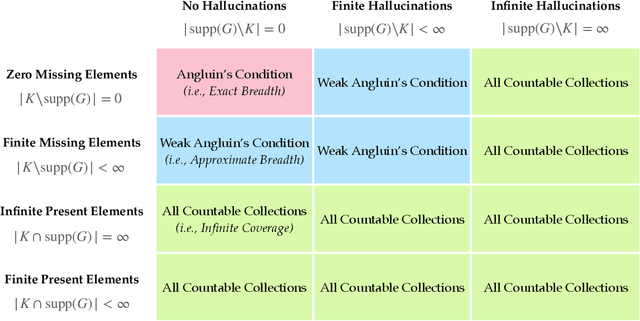
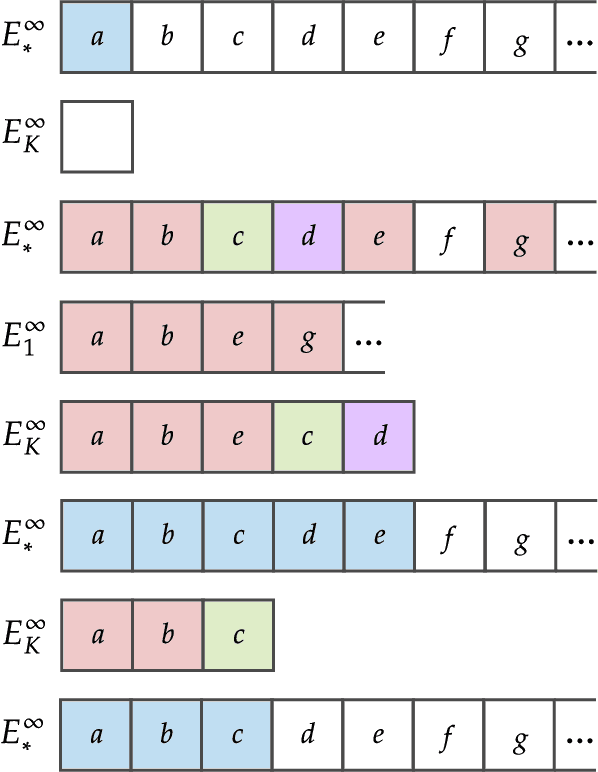
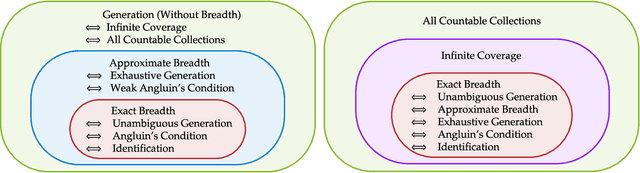
We study language generation in the limit, introduced by Kleinberg and Mullainathan [KM24], building on classical works of Gold [Gol67] and Angluin [Ang79]. [KM24] proposed an algorithm that generates strings from any countable language collection in the limit. While their algorithm eventually outputs strings from the target language $K$, it sacrifices breadth, i.e., the ability to generate all strings in $K$. A key open question in [KM24] is whether this trade-off between consistency and breadth is inherrent. Recent works proposed different notions of consistent generation with breadth. Kalavasis, Mehrotra, and Velegkas [KVM24] introduced three definitions: generation with exact breadth, approximate breadth, and unambiguous generation. Concurrently and independently, Charikar and Pabbaraju [CP24a] proposed exhaustive generation. Both works examined when generation with these notions of breadth is possible. Building on [CP24a, KVM24], we fully characterize language generation for these notions and their natural combinations. For exact breadth, we provide an unconditional lower bound, removing a technical condition from [KVM24] and extending the result of [CP24a] that holds for specific collections of languages. We show that generation with exact breadth is characterized by Angluin's condition for identification. We further introduce a weaker version of Angluin's condition that tightly characterizes both approximate breadth and exhaustive generation, proving their equivalence. Additionally, we show that unambiguous generation is also characterized by Angluin's condition as a special case of a broader result. Finally, we strengthen [KVM24] by giving unconditional lower bounds for stable generators, showing that Angluin's condition characterizes the previous breadth notions for stable generators. This shows a separation between stable and unstable generation with approximate breadth.

On the Limits of Language Generation: Trade-Offs Between Hallucination and Mode Collapse

Specifying all desirable properties of a language model is challenging, but certain requirements seem essential. Given samples from an unknown language, the trained model should produce valid strings not seen in training and be expressive enough to capture the language's full richness. Otherwise, outputting invalid strings constitutes "hallucination," and failing to capture the full range leads to "mode collapse." We ask if a language model can meet both requirements. We investigate this within a statistical language generation setting building on Gold and Angluin. Here, the model receives random samples from a distribution over an unknown language K, which belongs to a possibly infinite collection of languages. The goal is to generate unseen strings from K. We say the model generates from K with consistency and breadth if, as training size increases, its output converges to all unseen strings in K. Kleinberg and Mullainathan [KM24] asked if consistency and breadth in language generation are possible. We answer this negatively: for a large class of language models, including next-token prediction models, this is impossible for most collections of candidate languages. This contrasts with [KM24]'s result, showing consistent generation without breadth is possible for any countable collection of languages. Our finding highlights that generation with breadth fundamentally differs from generation without breadth. As a byproduct, we establish near-tight bounds on the number of samples needed for generation with or without breadth. Finally, our results offer hope: consistent generation with breadth is achievable for any countable collection of languages when negative examples (strings outside K) are available alongside positive ones. This suggests that post-training feedback, which encodes negative examples, can be crucial in reducing hallucinations while limiting mode collapse.

Barriers to Welfare Maximization with No-Regret Learning

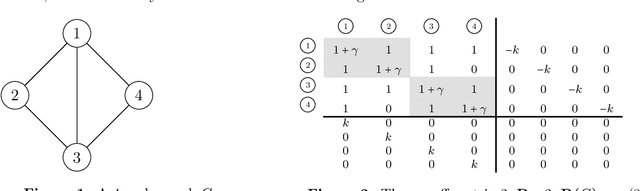
A celebrated result in the interface of online learning and game theory guarantees that the repeated interaction of no-regret players leads to a coarse correlated equilibrium (CCE) -- a natural game-theoretic solution concept. Despite the rich history of this foundational problem and the tremendous interest it has received in recent years, a basic question still remains open: how many iterations are needed for no-regret players to approximate an equilibrium? In this paper, we establish the first computational lower bounds for that problem in two-player (general-sum) games under the constraint that the CCE reached approximates the optimal social welfare (or some other natural objective). From a technical standpoint, our approach revolves around proving lower bounds for computing a near-optimal $T$-sparse CCE -- a mixture of $T$ product distributions, thereby circumscribing the iteration complexity of no-regret learning even in the centralized model of computation. Our proof proceeds by extending a classical reduction of Gilboa and Zemel [1989] for optimal Nash to sparse (approximate) CCE. In particular, we show that the inapproximability of maximum clique precludes attaining any non-trivial sparsity in polynomial time. Moreover, we strengthen our hardness results to apply in the low-precision regime as well via the planted clique conjecture.