Language Generation with Infinite Contamination

We study language generation in the limit, where an algorithm observes an adversarial enumeration of strings from an unknown target language $K$ and must eventually generate new, unseen strings from $K$. Kleinberg and Mullainathan [KM24] proved that generation is achievable in surprisingly general settings. But their generator suffers from ``mode collapse,'' producing from an ever-smaller subset of the target. To address this, Kleinberg and Wei [KW25] require the generator's output to be ``dense'' in the target language. They showed that generation with density, surprisingly, remains achievable at the same generality. Both results assume perfect data: no noisy insertions and no omissions. This raises a central question: how much contamination can generation tolerate? Recent works made partial progress on this question by studying (non-dense) generation with either finite amounts of noise (but no omissions) or omissions (but no noise). We characterize robustness under contaminated enumerations: 1. Generation under Contamination: Language generation in the limit is achievable for all countable collections iff the fraction of contaminated examples converges to zero. When this fails, we characterize which collections are generable. 2. Dense Generation under Contamination: Dense generation is strictly less robust to contamination than generation. As a byproduct, we resolve an open question of Raman and Raman [ICML25] by showing that generation is possible with only membership oracle access under finitely many contaminated examples. Finally, we introduce a beyond-worst-case model inspired by curriculum learning and prove that dense generation is achievable even with infinite contamination provided the fraction of contaminated examples converges to zero. This suggests curriculum learning may be crucial for learning from noisy web data.

Private Statistical Estimation via Truncation

We introduce a novel framework for differentially private (DP) statistical estimation via data truncation, addressing a key challenge in DP estimation when the data support is unbounded. Traditional approaches rely on problem-specific sensitivity analysis, limiting their applicability. By leveraging techniques from truncated statistics, we develop computationally efficient DP estimators for exponential family distributions, including Gaussian mean and covariance estimation, achieving near-optimal sample complexity. Previous works on exponential families only consider bounded or one-dimensional families. Our approach mitigates sensitivity through truncation while carefully correcting for the introduced bias using maximum likelihood estimation and DP stochastic gradient descent. Along the way, we establish improved uniform convergence guarantees for the log-likelihood function of exponential families, which may be of independent interest. Our results provide a general blueprint for DP algorithm design via truncated statistics.

Can SGD Select Good Fishermen? Local Convergence under Self-Selection Biases and Beyond

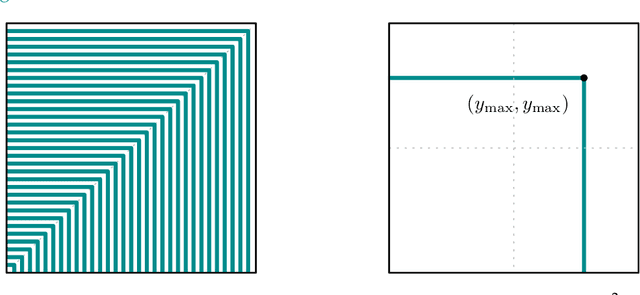
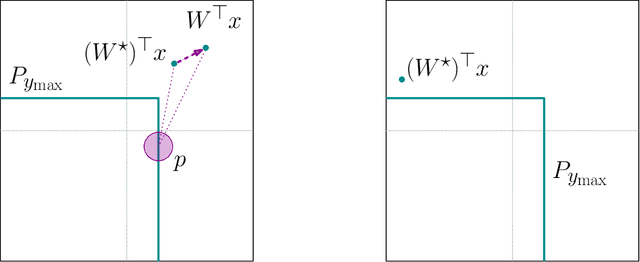
We revisit the problem of estimating $k$ linear regressors with self-selection bias in $d$ dimensions with the maximum selection criterion, as introduced by Cherapanamjeri, Daskalakis, Ilyas, and Zampetakis [CDIZ23, STOC'23]. Our main result is a $\operatorname{poly}(d,k,1/\varepsilon) + {k}^{O(k)}$ time algorithm for this problem, which yields an improvement in the running time of the algorithms of [CDIZ23] and [GM24, arXiv]. We achieve this by providing the first local convergence algorithm for self-selection, thus resolving the main open question of [CDIZ23]. To obtain this algorithm, we reduce self-selection to a seemingly unrelated statistical problem called coarsening. Coarsening occurs when one does not observe the exact value of the sample but only some set (a subset of the sample space) that contains the exact value. Inference from coarse samples arises in various real-world applications due to rounding by humans and algorithms, limited precision of instruments, and lag in multi-agent systems. Our reduction to coarsening is intuitive and relies on the geometry of the self-selection problem, which enables us to bypass the limitations of previous analytic approaches. To demonstrate its applicability, we provide a local convergence algorithm for linear regression under another self-selection criterion, which is related to second-price auction data. Further, we give the first polynomial time local convergence algorithm for coarse Gaussian mean estimation given samples generated from a convex partition. Previously, only a sample-efficient algorithm was known due to Fotakis, Kalavasis, Kontonis, and Tzamos [FKKT21, COLT'21].

On the Computational Landscape of Replicable Learning

We study computational aspects of algorithmic replicability, a notion of stability introduced by Impagliazzo, Lei, Pitassi, and Sorrell [2022]. Motivated by a recent line of work that established strong statistical connections between replicability and other notions of learnability such as online learning, private learning, and SQ learning, we aim to understand better the computational connections between replicability and these learning paradigms. Our first result shows that there is a concept class that is efficiently replicably PAC learnable, but, under standard cryptographic assumptions, no efficient online learner exists for this class. Subsequently, we design an efficient replicable learner for PAC learning parities when the marginal distribution is far from uniform, making progress on a question posed by Impagliazzo et al. [2022]. To obtain this result, we design a replicable lifting framework inspired by Blanc, Lange, Malik, and Tan [2023] that transforms in a black-box manner efficient replicable PAC learners under the uniform marginal distribution over the Boolean hypercube to replicable PAC learners under any marginal distribution, with sample and time complexity that depends on a certain measure of the complexity of the distribution. Finally, we show that any pure DP learner can be transformed to a replicable one in time polynomial in the accuracy, confidence parameters and exponential in the representation dimension of the underlying hypothesis class.

Replicable Learning of Large-Margin Halfspaces

We provide efficient replicable algorithms for the problem of learning large-margin halfspaces. Our results improve upon the algorithms provided by Impagliazzo, Lei, Pitassi, and Sorrell [STOC, 2022]. We design the first dimension-independent replicable algorithms for this task which runs in polynomial time, is proper, and has strictly improved sample complexity compared to the one achieved by Impagliazzo et al. [2022] with respect to all the relevant parameters. Moreover, our first algorithm has sample complexity that is optimal with respect to the accuracy parameter $\epsilon$. We also design an SGD-based replicable algorithm that, in some parameters' regimes, achieves better sample and time complexity than our first algorithm. Departing from the requirement of polynomial time algorithms, using the DP-to-Replicability reduction of Bun, Gaboardi, Hopkins, Impagliazzo, Lei, Pitassi, Sorrell, and Sivakumar [STOC, 2023], we show how to obtain a replicable algorithm for large-margin halfspaces with improved sample complexity with respect to the margin parameter $\tau$, but running time doubly exponential in $1/\tau^2$ and worse sample complexity dependence on $\epsilon$ than one of our previous algorithms. We then design an improved algorithm with better sample complexity than all three of our previous algorithms and running time exponential in $1/\tau^{2}$.

Replicability in Reinforcement Learning

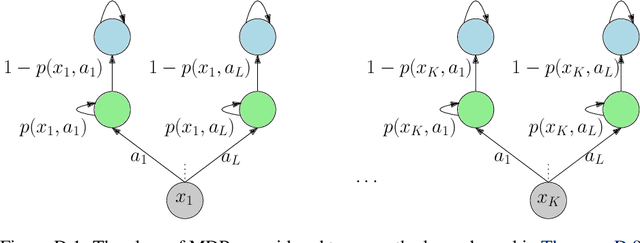
We initiate the mathematical study of replicability as an algorithmic property in the context of reinforcement learning (RL). We focus on the fundamental setting of discounted tabular MDPs with access to a generative model. Inspired by Impagliazzo et al. [2022], we say that an RL algorithm is replicable if, with high probability, it outputs the exact same policy after two executions on i.i.d. samples drawn from the generator when its internal randomness is the same. We first provide an efficient $\rho$-replicable algorithm for $(\varepsilon, \delta)$-optimal policy estimation with sample and time complexity $\widetilde O\left(\frac{N^3\cdot\log(1/\delta)}{(1-\gamma)^5\cdot\varepsilon^2\cdot\rho^2}\right)$, where $N$ is the number of state-action pairs. Next, for the subclass of deterministic algorithms, we provide a lower bound of order $\Omega\left(\frac{N^3}{(1-\gamma)^3\cdot\varepsilon^2\cdot\rho^2}\right)$. Then, we study a relaxed version of replicability proposed by Kalavasis et al. [2023] called TV indistinguishability. We design a computationally efficient TV indistinguishable algorithm for policy estimation whose sample complexity is $\widetilde O\left(\frac{N^2\cdot\log(1/\delta)}{(1-\gamma)^5\cdot\varepsilon^2\cdot\rho^2}\right)$. At the cost of $\exp(N)$ running time, we transform these TV indistinguishable algorithms to $\rho$-replicable ones without increasing their sample complexity. Finally, we introduce the notion of approximate-replicability where we only require that two outputted policies are close under an appropriate statistical divergence (e.g., Renyi) and show an improved sample complexity of $\widetilde O\left(\frac{N\cdot\log(1/\delta)}{(1-\gamma)^5\cdot\varepsilon^2\cdot\rho^2}\right)$.

Replicable Clustering

In this paper, we design replicable algorithms in the context of statistical clustering under the recently introduced notion of replicability. A clustering algorithm is replicable if, with high probability, it outputs the exact same clusters after two executions with datasets drawn from the same distribution when its internal randomness is shared across the executions. We propose such algorithms for the statistical $k$-medians, statistical $k$-means, and statistical $k$-centers problems by utilizing approximation routines for their combinatorial counterparts in a black-box manner. In particular, we demonstrate a replicable $O(1)$-approximation algorithm for statistical Euclidean $k$-medians ($k$-means) with $\operatorname{poly}(d)$ sample complexity. We also describe a $O(1)$-approximation algorithm with an additional $O(1)$-additive error for statistical Euclidean $k$-centers, albeit with $\exp(d)$ sample complexity.

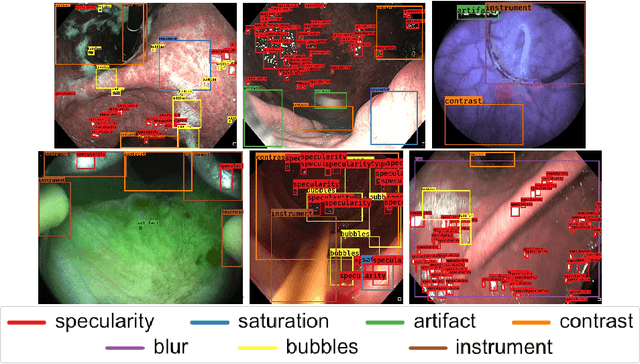
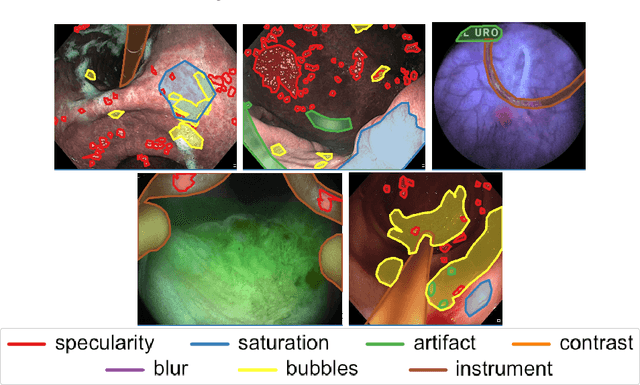
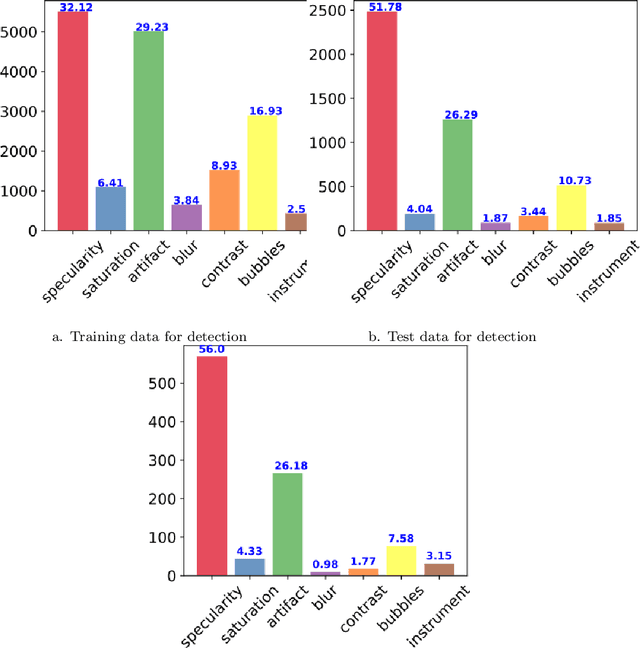
Endoscopy artifact detection (EAD 2019) challenge dataset

Endoscopic artifacts are a core challenge in facilitating the diagnosis and treatment of diseases in hollow organs. Precise detection of specific artifacts like pixel saturations, motion blur, specular reflections, bubbles and debris is essential for high-quality frame restoration and is crucial for realizing reliable computer-assisted tools for improved patient care. At present most videos in endoscopy are currently not analyzed due to the abundant presence of multi-class artifacts in video frames. Through the endoscopic artifact detection (EAD 2019) challenge, we address this key bottleneck problem by solving the accurate identification and localization of endoscopic frame artifacts to enable further key quantitative analysis of unusable video frames such as mosaicking and 3D reconstruction which is crucial for delivering improved patient care. This paper summarizes the challenge tasks and describes the dataset and evaluation criteria established in the EAD 2019 challenge.

A deep learning framework for quality assessment and restoration in video endoscopy

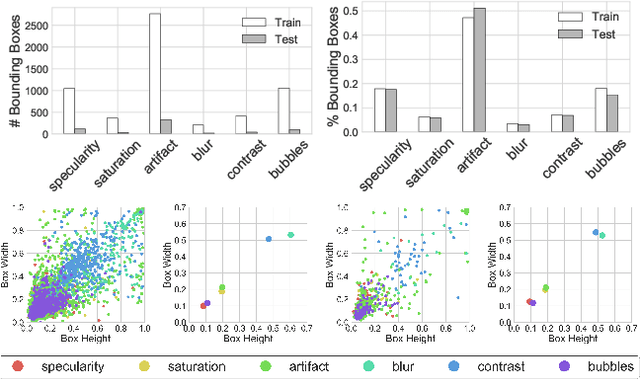
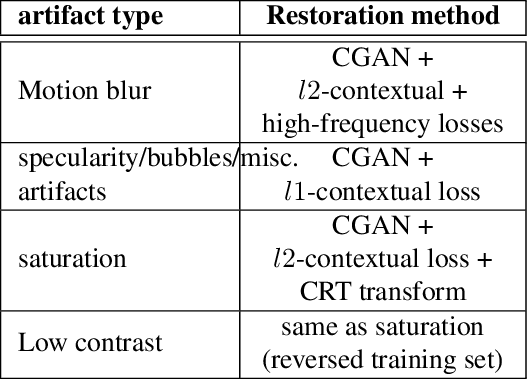
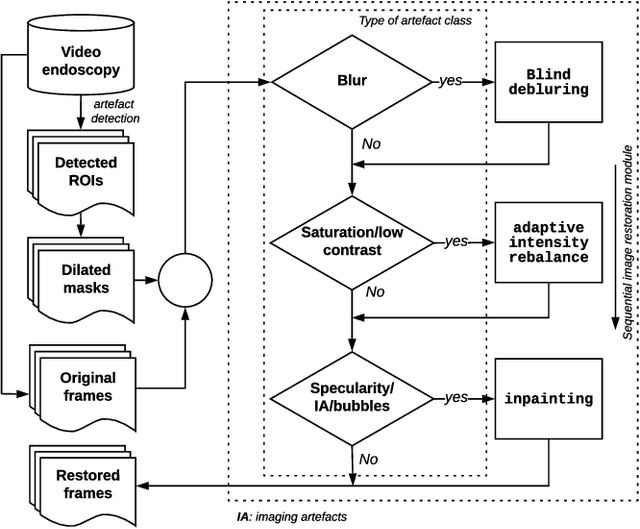
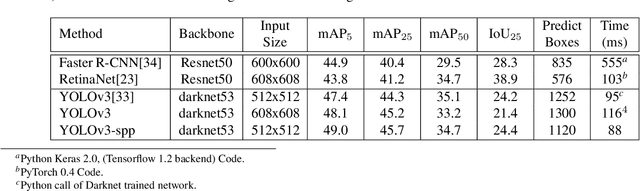
Endoscopy is a routine imaging technique used for both diagnosis and minimally invasive surgical treatment. Artifacts such as motion blur, bubbles, specular reflections, floating objects and pixel saturation impede the visual interpretation and the automated analysis of endoscopy videos. Given the widespread use of endoscopy in different clinical applications, we contend that the robust and reliable identification of such artifacts and the automated restoration of corrupted video frames is a fundamental medical imaging problem. Existing state-of-the-art methods only deal with the detection and restoration of selected artifacts. However, typically endoscopy videos contain numerous artifacts which motivates to establish a comprehensive solution. We propose a fully automatic framework that can: 1) detect and classify six different primary artifacts, 2) provide a quality score for each frame and 3) restore mildly corrupted frames. To detect different artifacts our framework exploits fast multi-scale, single stage convolutional neural network detector. We introduce a quality metric to assess frame quality and predict image restoration success. Generative adversarial networks with carefully chosen regularization are finally used to restore corrupted frames. Our detector yields the highest mean average precision (mAP at 5% threshold) of 49.0 and the lowest computational time of 88 ms allowing for accurate real-time processing. Our restoration models for blind deblurring, saturation correction and inpainting demonstrate significant improvements over previous methods. On a set of 10 test videos we show that our approach preserves an average of 68.7% which is 25% more frames than that retained from the raw videos.