Robust and differentially private stochastic linear bandits

In this paper, we study the stochastic linear bandit problem under the additional requirements of differential privacy, robustness and batched observations. In particular, we assume an adversary randomly chooses a constant fraction of the observed rewards in each batch, replacing them with arbitrary numbers. We present differentially private and robust variants of the arm elimination algorithm using logarithmic batch queries under two privacy models and provide regret bounds in both settings. In the first model, every reward in each round is reported by a potentially different client, which reduces to standard local differential privacy (LDP). In the second model, every action is "owned" by a different client, who may aggregate the rewards over multiple queries and privatize the aggregate response instead. To the best of our knowledge, our algorithms are the first simultaneously providing differential privacy and adversarial robustness in the stochastic linear bandits problem.

Replicable Clustering

In this paper, we design replicable algorithms in the context of statistical clustering under the recently introduced notion of replicability. A clustering algorithm is replicable if, with high probability, it outputs the exact same clusters after two executions with datasets drawn from the same distribution when its internal randomness is shared across the executions. We propose such algorithms for the statistical $k$-medians, statistical $k$-means, and statistical $k$-centers problems by utilizing approximation routines for their combinatorial counterparts in a black-box manner. In particular, we demonstrate a replicable $O(1)$-approximation algorithm for statistical Euclidean $k$-medians ($k$-means) with $\operatorname{poly}(d)$ sample complexity. We also describe a $O(1)$-approximation algorithm with an additional $O(1)$-additive error for statistical Euclidean $k$-centers, albeit with $\exp(d)$ sample complexity.

Reproducible Bandits

In this paper, we introduce the notion of reproducible policies in the context of stochastic bandits, one of the canonical problems in interactive learning. A policy in the bandit environment is called reproducible if it pulls, with high probability, the \emph{exact} same sequence of arms in two different and independent executions (i.e., under independent reward realizations). We show that not only do reproducible policies exist, but also they achieve almost the same optimal (non-reproducible) regret bounds in terms of the time horizon. More specifically, in the stochastic multi-armed bandits setting, we develop a policy with an optimal problem-dependent regret bound whose dependence on the reproducibility parameter is also optimal. Similarly, for stochastic linear bandits (with finitely and infinitely many arms) we develop reproducible policies that achieve the best-known problem-independent regret bounds with an optimal dependency on the reproducibility parameter. Our results show that even though randomization is crucial for the exploration-exploitation trade-off, an optimal balance can still be achieved while pulling the exact same arms in two different rounds of executions.

Smooth Anonymity for Sparse Binary Matrices

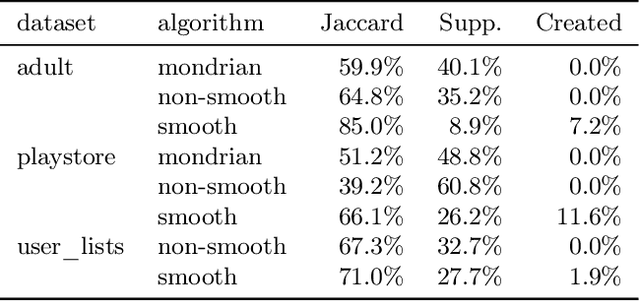
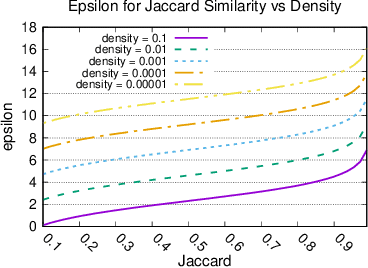
When working with user data providing well-defined privacy guarantees is paramount. In this work we aim to manipulate and share an entire sparse dataset with a third party privately. In fact, differential privacy has emerged as the gold standard of privacy, however, when it comes to sharing sparse datasets, as one of our main results, we prove that \emph{any} differentially private mechanism that maintains a reasonable similarity with the initial dataset is doomed to have a very weak privacy guarantee. Hence we need to opt for other privacy notions such as $k$-anonymity are better at preserving utility in this context. In this work we present a variation of $k$-anonymity, which we call smooth $k$-anonymity and design simple algorithms that efficiently provide smooth $k$-anonymity. We further perform an empirical evaluation to back our theoretical guarantees, and show that our algorithm improves the performance in downstream machine learning tasks on anonymized data.

Tackling Provably Hard Representative Selection via Graph Neural Networks

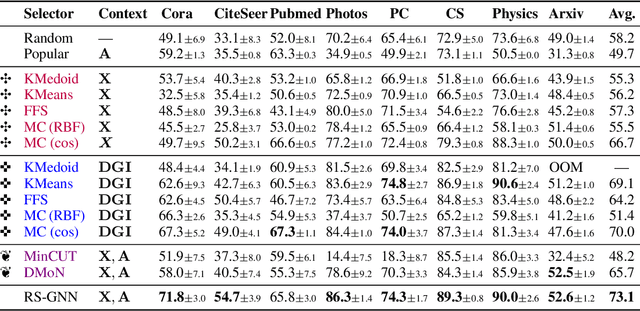
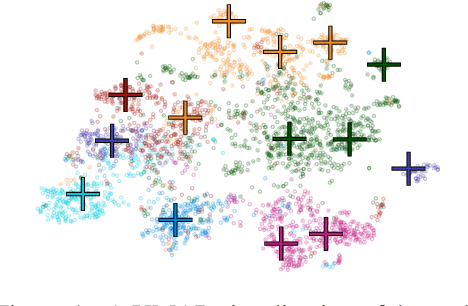
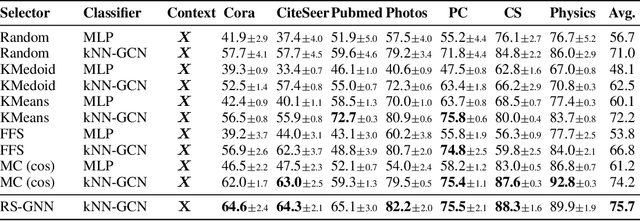
Representative selection (RS) is the problem of finding a small subset of exemplars from an unlabeled dataset, and has numerous applications in summarization, active learning, data compression and many other domains. In this paper, we focus on finding representatives that optimize the accuracy of a model trained on the selected representatives. We study RS for data represented as attributed graphs. We develop RS-GNN, a representation learning-based RS model based on Graph Neural Networks. Empirically, we demonstrate the effectiveness of RS-GNN on problems with predefined graph structures as well as problems with graphs induced from node feature similarities, by showing that RS-GNN achieves significant improvements over established baselines that optimize surrogate functions. Theoretically, we establish a new hardness result for RS by proving that RS is hard to approximate in polynomial time within any reasonable factor, which implies a significant gap between the optimum solution of widely-used surrogate functions and the actual accuracy of the model, and provides justification for the superiority of representation learning-based approaches such as RS-GNN over surrogate functions.

Improved Approximations for Euclidean $k$-means and $k$-median, via Nested Quasi-Independent Sets

Motivated by data analysis and machine learning applications, we consider the popular high-dimensional Euclidean $k$-median and $k$-means problems. We propose a new primal-dual algorithm, inspired by the classic algorithm of Jain and Vazirani and the recent algorithm of Ahmadian, Norouzi-Fard, Svensson, and Ward. Our algorithm achieves an approximation ratio of $2.406$ and $5.912$ for Euclidean $k$-median and $k$-means, respectively, improving upon the 2.633 approximation ratio of Ahmadian et al. and the 6.1291 approximation ratio of Grandoni, Ostrovsky, Rabani, Schulman, and Venkat. Our techniques involve a much stronger exploitation of the Euclidean metric than previous work on Euclidean clustering. In addition, we introduce a new method of removing excess centers using a variant of independent sets over graphs that we dub a "nested quasi-independent set". In turn, this technique may be of interest for other optimization problems in Euclidean and $\ell_p$ metric spaces.

Tight and Robust Private Mean Estimation with Few Users

In this work, we study high-dimensional mean estimation under user-level differential privacy, and attempt to design an $(\epsilon,\delta)$-differentially private mechanism using as few users as possible. In particular, we provide a nearly optimal trade-off between the number of users and the number of samples per user required for private mean estimation, even when the number of users is as low as $O(\frac{1}{\epsilon}\log\frac{1}{\delta})$. Interestingly our bound $O(\frac{1}{\epsilon}\log\frac{1}{\delta})$ on the number of users is independent of the dimension, unlike the previous work that depends polynomially on the dimension, solving a problem left open by Amin et al.~(ICML'2019). Our mechanism enjoys robustness up to the point that even if the information of $49\%$ of the users are corrupted, our final estimation is still approximately accurate. Finally, our results also apply to a broader range of problems such as learning discrete distributions, stochastic convex optimization, empirical risk minimization, and a variant of stochastic gradient descent via a reduction to differentially private mean estimation.

Label differential privacy via clustering

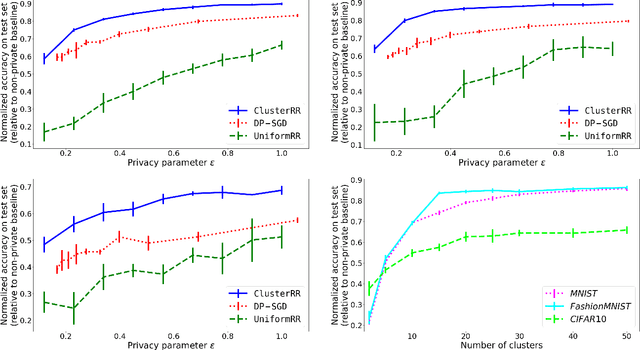
We present new mechanisms for \emph{label differential privacy}, a relaxation of differentially private machine learning that only protects the privacy of the labels in the training set. Our mechanisms cluster the examples in the training set using their (non-private) feature vectors, randomly re-sample each label from examples in the same cluster, and output a training set with noisy labels as well as a modified version of the true loss function. We prove that when the clusters are both large and high-quality, the model that minimizes the modified loss on the noisy training set converges to small excess risk at a rate that is comparable to the rate for non-private learning. We describe both a centralized mechanism in which the entire training set is stored by a trusted curator, and a distributed mechanism where each user stores a single labeled example and replaces her label with the label of a randomly selected user from the same cluster. We also describe a learning problem in which large clusters are necessary to achieve both strong privacy and either good precision or good recall. Our experiments show that randomizing the labels within each cluster significantly improves the privacy vs. accuracy trade-off compared to applying uniform randomized response to the labels, and also compared to learning a model via DP-SGD.

Almost Tight Approximation Algorithms for Explainable Clustering

Recently, due to an increasing interest for transparency in artificial intelligence, several methods of explainable machine learning have been developed with the simultaneous goal of accuracy and interpretability by humans. In this paper, we study a recent framework of explainable clustering first suggested by Dasgupta et al.~\cite{dasgupta2020explainable}. Specifically, we focus on the $k$-means and $k$-medians problems and provide nearly tight upper and lower bounds. First, we provide an $O(\log k \log \log k)$-approximation algorithm for explainable $k$-medians, improving on the best known algorithm of $O(k)$~\cite{dasgupta2020explainable} and nearly matching the known $\Omega(\log k)$ lower bound~\cite{dasgupta2020explainable}. In addition, in low-dimensional spaces $d \ll \log k$, we show that our algorithm also provides an $O(d \log^2 d)$-approximate solution for explainable $k$-medians. This improves over the best known bound of $O(d \log k)$ for low dimensions~\cite{laber2021explainable}, and is a constant for constant dimensional spaces. To complement this, we show a nearly matching $\Omega(d)$ lower bound. Next, we study the $k$-means problem in this context and provide an $O(k \log k)$-approximation algorithm for explainable $k$-means, improving over the $O(k^2)$ bound of Dasgupta et al. and the $O(d k \log k)$ bound of \cite{laber2021explainable}. To complement this we provide an almost tight $\Omega(k)$ lower bound, improving over the $\Omega(\log k)$ lower bound of Dasgupta et al. Given an approximate solution to the classic $k$-means and $k$-medians, our algorithm for $k$-medians runs in time $O(kd \log^2 k )$ and our algorithm for $k$-means runs in time $ O(k^2 d)$.

Feature Cross Search via Submodular Optimization

In this paper, we study feature cross search as a fundamental primitive in feature engineering. The importance of feature cross search especially for the linear model has been known for a while, with well-known textbook examples. In this problem, the goal is to select a small subset of features, combine them to form a new feature (called the crossed feature) by considering their Cartesian product, and find feature crosses to learn an \emph{accurate} model. In particular, we study the problem of maximizing a normalized Area Under the Curve (AUC) of the linear model trained on the crossed feature column. First, we show that it is not possible to provide an $n^{1/\log\log n}$-approximation algorithm for this problem unless the exponential time hypothesis fails. This result also rules out the possibility of solving this problem in polynomial time unless $\mathsf{P}=\mathsf{NP}$. On the positive side, by assuming the \naive\ assumption, we show that there exists a simple greedy $(1-1/e)$-approximation algorithm for this problem. This result is established by relating the AUC to the total variation of the commutator of two probability measures and showing that the total variation of the commutator is monotone and submodular. To show this, we relate the submodularity of this function to the positive semi-definiteness of a corresponding kernel matrix. Then, we use Bochner's theorem to prove the positive semi-definiteness by showing that its inverse Fourier transform is non-negative everywhere. Our techniques and structural results might be of independent interest.