Learning from Synthetic Data: Limitations of ERM

The prevalence and low cost of LLMs have led to a rise of synthetic content. From review sites to court documents, ``natural'' content has been contaminated by data points that appear similar to natural data, but are in fact LLM-generated. In this work we revisit fundamental learning theory questions in this, now ubiquitous, setting. We model this scenario as a sequence of learning tasks where the input is a mix of natural and synthetic data, and the learning algorithms are oblivious to the origin of any individual example. We study the possibilities and limitations of ERM in this setting. For the problem of estimating the mean of an arbitrary $d$-dimensional distribution, we find that while ERM converges to the true mean, it is outperformed by an algorithm that assigns non-uniform weights to examples from different generations of data. For the PAC learning setting, the disparity is even more stark. We find that ERM does not always converge to the true concept, echoing the model collapse literature. However, we show there are algorithms capable of learning the correct hypothesis for arbitrary VC classes and arbitrary amounts of contamination.

An Optimization Framework for Differentially Private Sparse Fine-Tuning

Differentially private stochastic gradient descent (DP-SGD) is broadly considered to be the gold standard for training and fine-tuning neural networks under differential privacy (DP). With the increasing availability of high-quality pre-trained model checkpoints (e.g., vision and language models), fine-tuning has become a popular strategy. However, despite recent progress in understanding and applying DP-SGD for private transfer learning tasks, significant challenges remain -- most notably, the performance gap between models fine-tuned with DP-SGD and their non-private counterparts. Sparse fine-tuning on private data has emerged as an alternative to full-model fine-tuning; recent work has shown that privately fine-tuning only a small subset of model weights and keeping the rest of the weights fixed can lead to better performance. In this work, we propose a new approach for sparse fine-tuning of neural networks under DP. Existing work on private sparse finetuning often used fixed choice of trainable weights (e.g., updating only the last layer), or relied on public model's weights to choose the subset of weights to modify. Such choice of weights remains suboptimal. In contrast, we explore an optimization-based approach, where our selection method makes use of the private gradient information, while using off the shelf privacy accounting techniques. Our numerical experiments on several computer vision models and datasets show that our selection method leads to better prediction accuracy, compared to full-model private fine-tuning or existing private sparse fine-tuning approaches.

Escaping Collapse: The Strength of Weak Data for Large Language Model Training

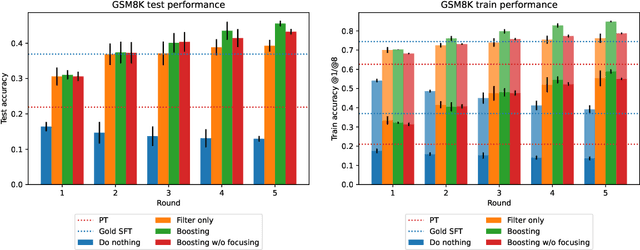
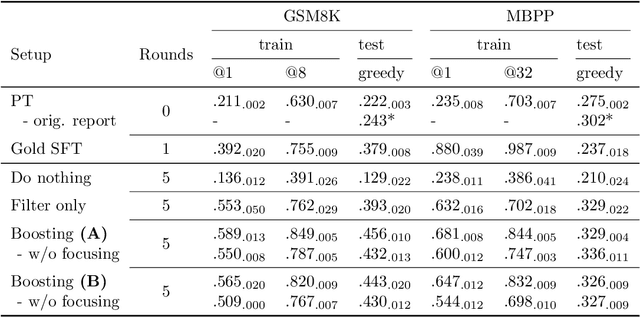
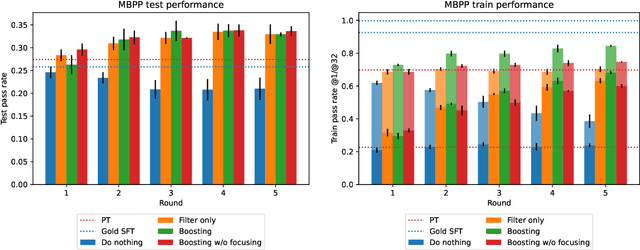
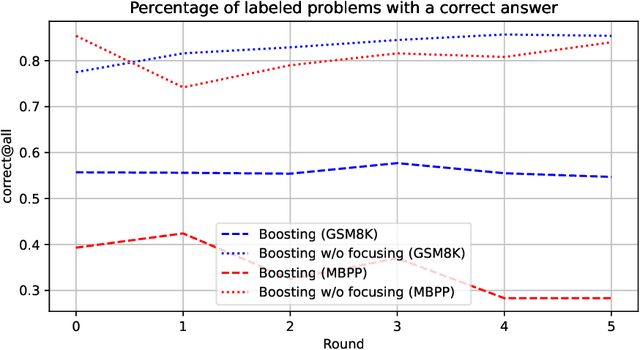
Synthetically-generated data plays an increasingly larger role in training large language models. However, while synthetic data has been found to be useful, studies have also shown that without proper curation it can cause LLM performance to plateau, or even "collapse", after many training iterations. In this paper, we formalize this question and develop a theoretical framework to investigate how much curation is needed in order to ensure that LLM performance continually improves. We find that the requirements are nearly minimal. We describe a training procedure that converges to an optimal LLM even if almost all of the non-synthetic training data is of poor quality. Our analysis is inspired by boosting, a classic machine learning technique that leverages a very weak learning algorithm to produce an arbitrarily good classifier. Our training procedure subsumes many recently proposed methods for training LLMs on synthetic data, and thus our analysis sheds light on why they are successful, and also suggests opportunities for future improvement. We present experiments that validate our theory, and show that dynamically focusing labeling resources on the most challenging examples -- in much the same way that boosting focuses the efforts of the weak learner -- leads to improved performance.

Binary Search with Distributional Predictions

Algorithms with (machine-learned) predictions is a powerful framework for combining traditional worst-case algorithms with modern machine learning. However, the vast majority of work in this space assumes that the prediction itself is non-probabilistic, even if it is generated by some stochastic process (such as a machine learning system). This is a poor fit for modern ML, particularly modern neural networks, which naturally generate a distribution. We initiate the study of algorithms with distributional predictions, where the prediction itself is a distribution. We focus on one of the simplest yet fundamental settings: binary search (or searching a sorted array). This setting has one of the simplest algorithms with a point prediction, but what happens if the prediction is a distribution? We show that this is a richer setting: there are simple distributions where using the classical prediction-based algorithm with any single prediction does poorly. Motivated by this, as our main result, we give an algorithm with query complexity $O(H(p) + \log \eta)$, where $H(p)$ is the entropy of the true distribution $p$ and $\eta$ is the earth mover's distance between $p$ and the predicted distribution $\hat p$. This also yields the first distributionally-robust algorithm for the classical problem of computing an optimal binary search tree given a distribution over target keys. We complement this with a lower bound showing that this query complexity is essentially optimal (up to constants), and experiments validating the practical usefulness of our algorithm.

Private prediction for large-scale synthetic text generation

We present an approach for generating differentially private synthetic text using large language models (LLMs), via private prediction. In the private prediction framework, we only require the output synthetic data to satisfy differential privacy guarantees. This is in contrast to approaches that train a generative model on potentially sensitive user-supplied source data and seek to ensure the model itself is safe to release. We prompt a pretrained LLM with source data, but ensure that next-token predictions are made with differential privacy guarantees. Previous work in this paradigm reported generating a small number of examples (<10) at reasonable privacy levels, an amount of data that is useful only for downstream in-context learning or prompting. In contrast, we make changes that allow us to generate thousands of high-quality synthetic data points, greatly expanding the set of potential applications. Our improvements come from an improved privacy analysis and a better private selection mechanism, which makes use of the equivalence between the softmax layer for sampling tokens in LLMs and the exponential mechanism. Furthermore, we introduce a novel use of public predictions via the sparse vector technique, in which we do not pay privacy costs for tokens that are predictable without sensitive data; we find this to be particularly effective for structured data.

Warm-starting Push-Relabel

Push-Relabel is one of the most celebrated network flow algorithms. Maintaining a pre-flow that saturates a cut, it enjoys better theoretical and empirical running time than other flow algorithms, such as Ford-Fulkerson. In practice, Push-Relabel is even faster than what theoretical guarantees can promise, in part because of the use of good heuristics for seeding and updating the iterative algorithm. However, it remains unclear how to run Push-Relabel on an arbitrary initialization that is not necessarily a pre-flow or cut-saturating. We provide the first theoretical guarantees for warm-starting Push-Relabel with a predicted flow, where our learning-augmented version benefits from fast running time when the predicted flow is close to an optimal flow, while maintaining robust worst-case guarantees. Interestingly, our algorithm uses the gap relabeling heuristic, which has long been employed in practice, even though prior to our work there was no rigorous theoretical justification for why it can lead to run-time improvements. We then provide experiments that show our warm-started Push-Relabel also works well in practice.

Scaling Laws for Downstream Task Performance of Large Language Models

Scaling laws provide important insights that can guide the design of large language models (LLMs). Existing work has primarily focused on studying scaling laws for pretraining (upstream) loss. However, in transfer learning settings, in which LLMs are pretrained on an unsupervised dataset and then finetuned on a downstream task, we often also care about the downstream performance. In this work, we study the scaling behavior in a transfer learning setting, where LLMs are finetuned for machine translation tasks. Specifically, we investigate how the choice of the pretraining data and its size affect downstream performance (translation quality) as judged by two metrics: downstream cross-entropy and BLEU score. Our experiments indicate that the size of the finetuning dataset and the distribution alignment between the pretraining and downstream data significantly influence the scaling behavior. With sufficient alignment, both downstream cross-entropy and BLEU score improve monotonically with more pretraining data. In such cases, we show that it is possible to predict the downstream BLEU score with good accuracy using a log-law. However, there are also cases where moderate misalignment causes the BLEU score to fluctuate or get worse with more pretraining, whereas downstream cross-entropy monotonically improves. By analyzing these observations, we provide new practical insights for choosing appropriate pretraining data.

Measuring Re-identification Risk

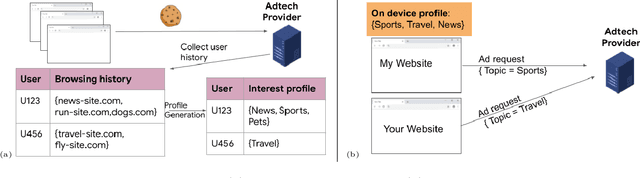
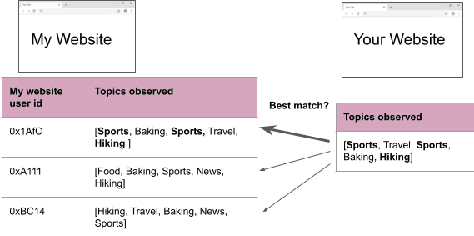
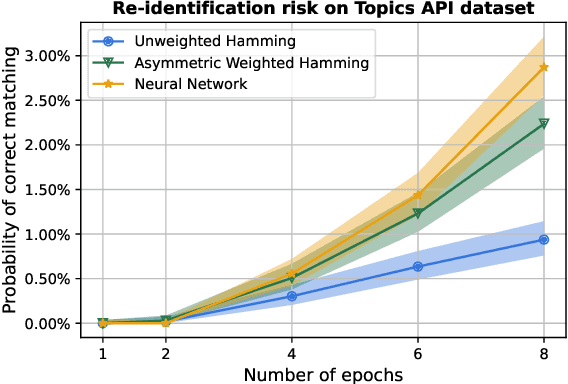
Compact user representations (such as embeddings) form the backbone of personalization services. In this work, we present a new theoretical framework to measure re-identification risk in such user representations. Our framework, based on hypothesis testing, formally bounds the probability that an attacker may be able to obtain the identity of a user from their representation. As an application, we show how our framework is general enough to model important real-world applications such as the Chrome's Topics API for interest-based advertising. We complement our theoretical bounds by showing provably good attack algorithms for re-identification that we use to estimate the re-identification risk in the Topics API. We believe this work provides a rigorous and interpretable notion of re-identification risk and a framework to measure it that can be used to inform real-world applications.

How to DP-fy ML: A Practical Guide to Machine Learning with Differential Privacy

ML models are ubiquitous in real world applications and are a constant focus of research. At the same time, the community has started to realize the importance of protecting the privacy of ML training data. Differential Privacy (DP) has become a gold standard for making formal statements about data anonymization. However, while some adoption of DP has happened in industry, attempts to apply DP to real world complex ML models are still few and far between. The adoption of DP is hindered by limited practical guidance of what DP protection entails, what privacy guarantees to aim for, and the difficulty of achieving good privacy-utility-computation trade-offs for ML models. Tricks for tuning and maximizing performance are scattered among papers or stored in the heads of practitioners. Furthermore, the literature seems to present conflicting evidence on how and whether to apply architectural adjustments and which components are "safe" to use with DP. This work is a self-contained guide that gives an in-depth overview of the field of DP ML and presents information about achieving the best possible DP ML model with rigorous privacy guarantees. Our target audience is both researchers and practitioners. Researchers interested in DP for ML will benefit from a clear overview of current advances and areas for improvement. We include theory-focused sections that highlight important topics such as privacy accounting and its assumptions, and convergence. For a practitioner, we provide a background in DP theory and a clear step-by-step guide for choosing an appropriate privacy definition and approach, implementing DP training, potentially updating the model architecture, and tuning hyperparameters. For both researchers and practitioners, consistently and fully reporting privacy guarantees is critical, and so we propose a set of specific best practices for stating guarantees.

Private Algorithms with Private Predictions

When applying differential privacy to sensitive data, a common way of getting improved performance is to use external information such as other sensitive data, public data, or human priors. We propose to use the algorithms with predictions framework -- previously applied largely to improve time complexity or competitive ratios -- as a powerful way of designing and analyzing privacy-preserving methods that can take advantage of such external information to improve utility. For four important tasks -- quantile release, its extension to multiple quantiles, covariance estimation, and data release -- we construct prediction-dependent differentially private methods whose utility scales with natural measures of prediction quality. The analyses enjoy several advantages, including minimal assumptions about the data, natural ways of adding robustness to noisy predictions, and novel "meta" algorithms that can learn predictions from other (potentially sensitive) data. Overall, our results demonstrate how to enable differentially private algorithms to make use of and learn noisy predictions, which holds great promise for improving utility while preserving privacy across a variety of tasks.