Reasoning Models Can be Accurately Pruned Via Chain-of-Thought Reconstruction

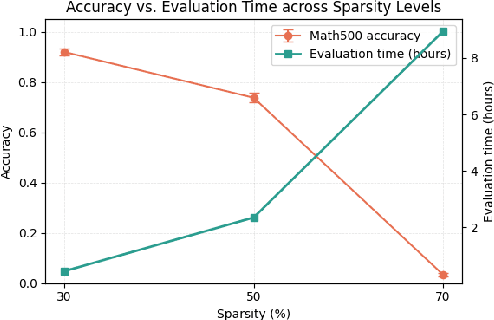
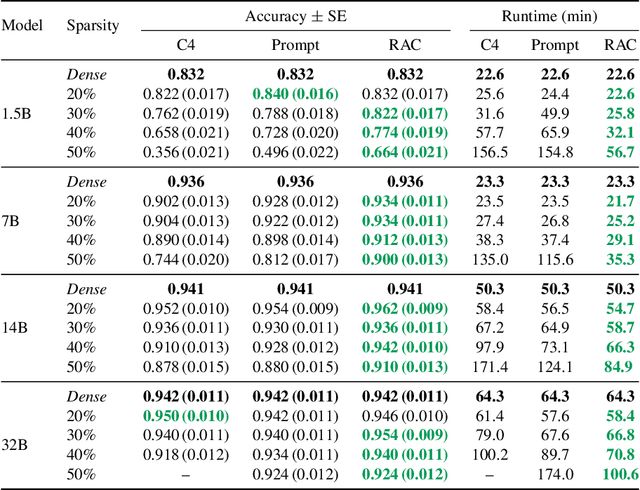
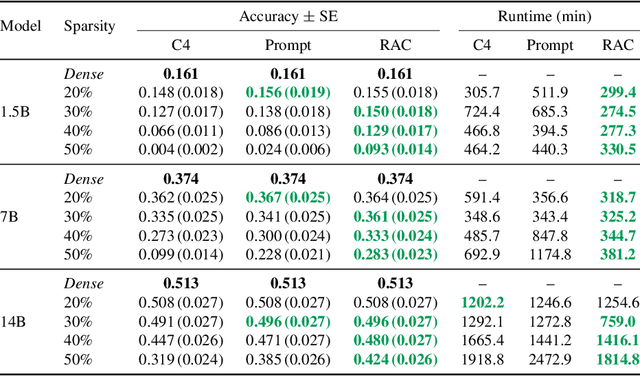
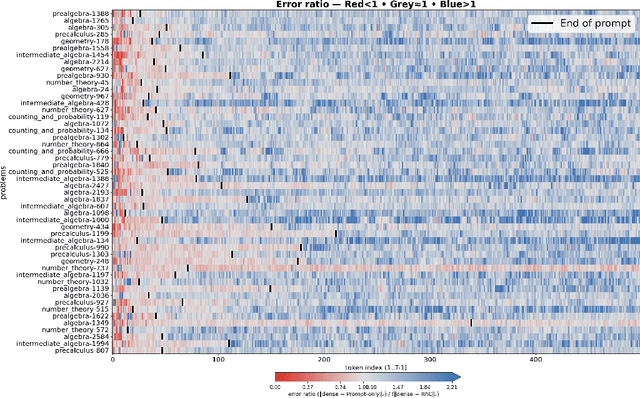
Reasoning language models such as DeepSeek-R1 produce long chain-of-thought traces during inference time which make them costly to deploy at scale. We show that using compression techniques such as neural network pruning produces greater performance loss than in typical language modeling tasks, and in some cases can make the model slower since they cause the model to produce more thinking tokens but with worse performance. We show that this is partly due to the fact that standard LLM pruning methods often focus on input reconstruction, whereas reasoning is a decode-dominated task. We introduce a simple, drop-in fix: during pruning we jointly reconstruct activations from the input and the model's on-policy chain-of-thought traces. This "Reasoning-Aware Compression" (RAC) integrates seamlessly into existing pruning workflows such as SparseGPT, and boosts their performance significantly. Code reproducing the results in the paper can be found at: https://github.com/RyanLucas3/RAC

BP-Seg: A graphical model approach to unsupervised and non-contiguous text segmentation using belief propagation

Text segmentation based on the semantic meaning of sentences is a fundamental task with broad utility in many downstream applications. In this paper, we propose a graphical model-based unsupervised learning approach, named BP-Seg for efficient text segmentation. Our method not only considers local coherence, capturing the intuition that adjacent sentences are often more related, but also effectively groups sentences that are distant in the text yet semantically similar. This is achieved through belief propagation on the carefully constructed graphical models. Experimental results on both an illustrative example and a dataset with long-form documents demonstrate that our method performs favorably compared to competing approaches.

An Optimization Framework for Differentially Private Sparse Fine-Tuning

Differentially private stochastic gradient descent (DP-SGD) is broadly considered to be the gold standard for training and fine-tuning neural networks under differential privacy (DP). With the increasing availability of high-quality pre-trained model checkpoints (e.g., vision and language models), fine-tuning has become a popular strategy. However, despite recent progress in understanding and applying DP-SGD for private transfer learning tasks, significant challenges remain -- most notably, the performance gap between models fine-tuned with DP-SGD and their non-private counterparts. Sparse fine-tuning on private data has emerged as an alternative to full-model fine-tuning; recent work has shown that privately fine-tuning only a small subset of model weights and keeping the rest of the weights fixed can lead to better performance. In this work, we propose a new approach for sparse fine-tuning of neural networks under DP. Existing work on private sparse finetuning often used fixed choice of trainable weights (e.g., updating only the last layer), or relied on public model's weights to choose the subset of weights to modify. Such choice of weights remains suboptimal. In contrast, we explore an optimization-based approach, where our selection method makes use of the private gradient information, while using off the shelf privacy accounting techniques. Our numerical experiments on several computer vision models and datasets show that our selection method leads to better prediction accuracy, compared to full-model private fine-tuning or existing private sparse fine-tuning approaches.

Efficient AI in Practice: Training and Deployment of Efficient LLMs for Industry Applications

Large language models (LLMs) have demonstrated remarkable performance across a wide range of industrial applications, from search and recommendations to generative tasks. Although scaling laws indicate that larger models generally yield better generalization and performance, their substantial computational requirements often render them impractical for many real-world scenarios at scale. In this paper, we present methods and insights for training small language models (SLMs) that deliver high performance and efficiency in deployment. We focus on two key techniques: (1) knowledge distillation and (2) model compression via quantization and pruning. These approaches enable SLMs to retain much of the quality of their larger counterparts while significantly reducing training, serving costs, and latency. We detail the impact of these techniques on a variety of use cases at a large professional social network platform and share deployment lessons - including hardware optimization strategies that enhance speed and throughput for both predictive and reasoning-based applications.

HASSLE-free: A unified Framework for Sparse plus Low-Rank Matrix Decomposition for LLMs

The impressive capabilities of large foundation models come at a cost of substantial computing resources to serve them. Compressing these pre-trained models is of practical interest as it can democratize deploying them to the machine learning community at large by lowering the costs associated with inference. A promising compression scheme is to decompose foundation models' dense weights into a sum of sparse plus low-rank matrices. In this paper, we design a unified framework coined HASSLE-free for (semi-structured) sparse plus low-rank matrix decomposition of foundation models. Our framework introduces the local layer-wise reconstruction error objective for this decomposition, we demonstrate that prior work solves a relaxation of this optimization problem; and we provide efficient and scalable methods to minimize the exact introduced optimization problem. HASSLE-free substantially outperforms state-of-the-art methods in terms of the introduced objective and a wide range of LLM evaluation benchmarks. For the Llama3-8B model with a 2:4 sparsity component plus a 64-rank component decomposition, a compression scheme for which recent work shows important inference acceleration on GPUs, HASSLE-free reduces the test perplexity by 12% for the WikiText-2 dataset and reduces the gap (compared to the dense model) of the average of eight popular zero-shot tasks by 15% compared to existing methods.

ALPS: Improved Optimization for Highly Sparse One-Shot Pruning for Large Language Models

The impressive performance of Large Language Models (LLMs) across various natural language processing tasks comes at the cost of vast computational resources and storage requirements. One-shot pruning techniques offer a way to alleviate these burdens by removing redundant weights without the need for retraining. Yet, the massive scale of LLMs often forces current pruning approaches to rely on heuristics instead of optimization-based techniques, potentially resulting in suboptimal compression. In this paper, we introduce ALPS, an optimization-based framework that tackles the pruning problem using the operator splitting technique and a preconditioned conjugate gradient-based post-processing step. Our approach incorporates novel techniques to accelerate and theoretically guarantee convergence while leveraging vectorization and GPU parallelism for efficiency. ALPS substantially outperforms state-of-the-art methods in terms of the pruning objective and perplexity reduction, particularly for highly sparse models. On the OPT-30B model with 70% sparsity, ALPS achieves a 13% reduction in test perplexity on the WikiText dataset and a 19% improvement in zero-shot benchmark performance compared to existing methods.

End-to-end Feature Selection Approach for Learning Skinny Trees

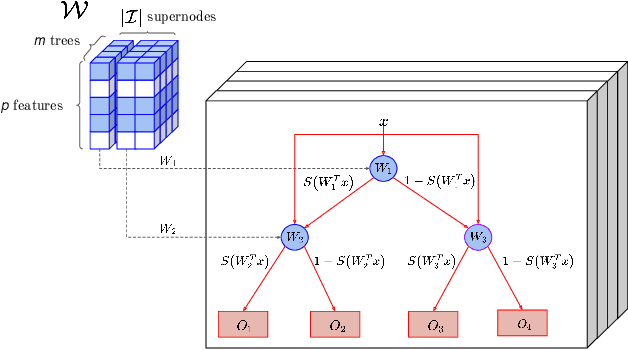
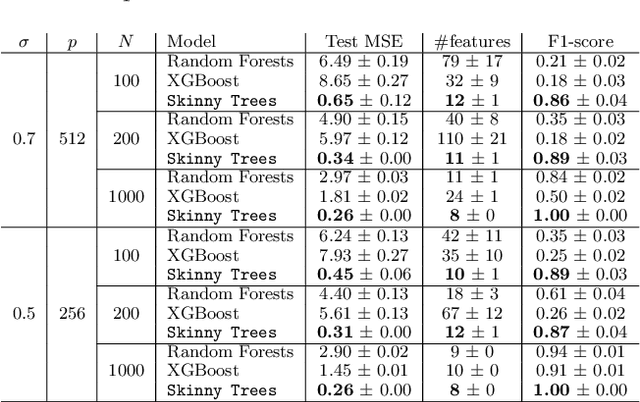
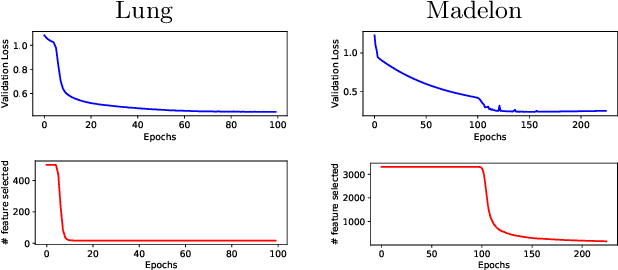
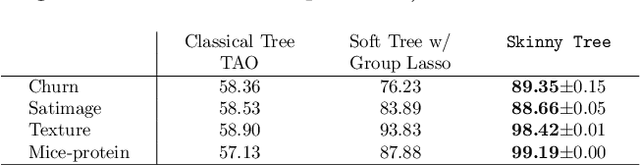
Joint feature selection and tree ensemble learning is a challenging task. Popular tree ensemble toolkits e.g., Gradient Boosted Trees and Random Forests support feature selection post-training based on feature importances, which are known to be misleading, and can significantly hurt performance. We propose Skinny Trees: a toolkit for feature selection in tree ensembles, such that feature selection and tree ensemble learning occurs simultaneously. It is based on an end-to-end optimization approach that considers feature selection in differentiable trees with Group $\ell_0 - \ell_2$ regularization. We optimize with a first-order proximal method and present convergence guarantees for a non-convex and non-smooth objective. Interestingly, dense-to-sparse regularization scheduling can lead to more expressive and sparser tree ensembles than vanilla proximal method. On 15 synthetic and real-world datasets, Skinny Trees can achieve $1.5\times$ - $620\times$ feature compression rates, leading up to $10\times$ faster inference over dense trees, without any loss in performance. Skinny Trees lead to superior feature selection than many existing toolkits e.g., in terms of AUC performance for $25\%$ feature budget, Skinny Trees outperforms LightGBM by $10.2\%$ (up to $37.7\%$), and Random Forests by $3\%$ (up to $12.5\%$).

QuantEase: Optimization-based Quantization for Language Models -- An Efficient and Intuitive Algorithm

With the rising popularity of Large Language Models (LLMs), there has been an increasing interest in compression techniques that enable their efficient deployment. This study focuses on the Post-Training Quantization (PTQ) of LLMs. Drawing from recent advances, our work introduces QuantEase, a layer-wise quantization framework where individual layers undergo separate quantization. The problem is framed as a discrete-structured non-convex optimization, prompting the development of algorithms rooted in Coordinate Descent (CD) techniques. These CD-based methods provide high-quality solutions to the complex non-convex layer-wise quantization problems. Notably, our CD-based approach features straightforward updates, relying solely on matrix and vector operations, circumventing the need for matrix inversion or decomposition. We also explore an outlier-aware variant of our approach, allowing for retaining significant weights (outliers) with complete precision. Our proposal attains state-of-the-art performance in terms of perplexity and zero-shot accuracy in empirical evaluations across various LLMs and datasets, with relative improvements up to 15% over methods such as GPTQ. Particularly noteworthy is our outlier-aware algorithm's capability to achieve near or sub-3-bit quantization of LLMs with an acceptable drop in accuracy, obviating the need for non-uniform quantization or grouping techniques, improving upon methods such as SpQR by up to two times in terms of perplexity.

Sparse Gaussian Graphical Models with Discrete Optimization: Computational and Statistical Perspectives

We consider the problem of learning a sparse graph underlying an undirected Gaussian graphical model, a key problem in statistical machine learning. Given $n$ samples from a multivariate Gaussian distribution with $p$ variables, the goal is to estimate the $p \times p$ inverse covariance matrix (aka precision matrix), assuming it is sparse (i.e., has a few nonzero entries). We propose GraphL0BnB, a new estimator based on an $\ell_0$-penalized version of the pseudolikelihood function, while most earlier approaches are based on the $\ell_1$-relaxation. Our estimator can be formulated as a convex mixed integer program (MIP) which can be difficult to compute at scale using off-the-shelf commercial solvers. To solve the MIP, we propose a custom nonlinear branch-and-bound (BnB) framework that solves node relaxations with tailored first-order methods. As a by-product of our BnB framework, we propose large-scale solvers for obtaining good primal solutions that are of independent interest. We derive novel statistical guarantees (estimation and variable selection) for our estimator and discuss how our approach improves upon existing estimators. Our numerical experiments on real/synthetic datasets suggest that our method can solve, to near-optimality, problem instances with $p = 10^4$ -- corresponding to a symmetric matrix of size $p \times p$ with $p^2/2$ binary variables. We demonstrate the usefulness of GraphL0BnB versus various state-of-the-art approaches on a range of datasets.

Sharpness-Aware Minimization: An Implicit Regularization Perspective

Sharpness-Aware Minimization (SAM) is a recent optimization framework aiming to improve the deep neural network generalization, through obtaining flatter (i.e. less sharp) solutions. As SAM has been numerically successful, recent papers have studied the theoretical aspects of the framework. In this work, we study SAM through an implicit regularization lens, and present a new theoretical explanation of why SAM generalizes well. To this end, we study the least-squares linear regression problem and show a bias-variance trade-off for SAM's error over the course of the algorithm. We show SAM has lower bias compared to Gradient Descent (GD), while having higher variance. This shows SAM can outperform GD, specially if the algorithm is \emph{stopped early}, which is often the case when training large neural networks due to the prohibitive computational cost. We extend our results to kernel regression, as well as stochastic optimization and discuss how implicit regularization of SAM can improve upon vanilla training.