A Precise Characterization of SGD Stability Using Loss Surface Geometry

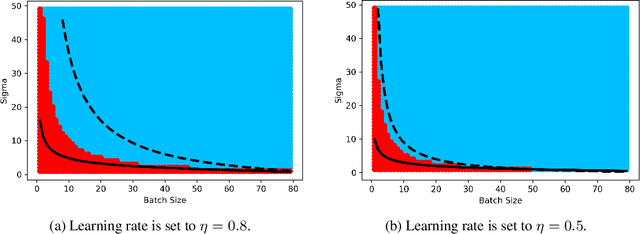
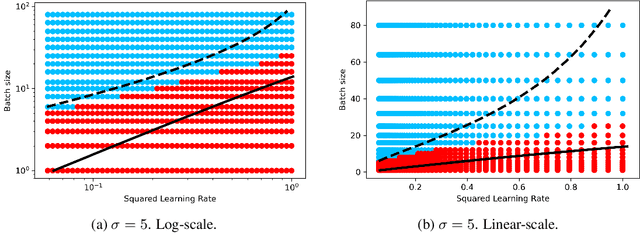
Stochastic Gradient Descent (SGD) stands as a cornerstone optimization algorithm with proven real-world empirical successes but relatively limited theoretical understanding. Recent research has illuminated a key factor contributing to its practical efficacy: the implicit regularization it instigates. Several studies have investigated the linear stability property of SGD in the vicinity of a stationary point as a predictive proxy for sharpness and generalization error in overparameterized neural networks (Wu et al., 2022; Jastrzebski et al., 2019; Cohen et al., 2021). In this paper, we delve deeper into the relationship between linear stability and sharpness. More specifically, we meticulously delineate the necessary and sufficient conditions for linear stability, contingent on hyperparameters of SGD and the sharpness at the optimum. Towards this end, we introduce a novel coherence measure of the loss Hessian that encapsulates pertinent geometric properties of the loss function that are relevant to the linear stability of SGD. It enables us to provide a simplified sufficient condition for identifying linear instability at an optimum. Notably, compared to previous works, our analysis relies on significantly milder assumptions and is applicable for a broader class of loss functions than known before, encompassing not only mean-squared error but also cross-entropy loss.

QuantEase: Optimization-based Quantization for Language Models -- An Efficient and Intuitive Algorithm

With the rising popularity of Large Language Models (LLMs), there has been an increasing interest in compression techniques that enable their efficient deployment. This study focuses on the Post-Training Quantization (PTQ) of LLMs. Drawing from recent advances, our work introduces QuantEase, a layer-wise quantization framework where individual layers undergo separate quantization. The problem is framed as a discrete-structured non-convex optimization, prompting the development of algorithms rooted in Coordinate Descent (CD) techniques. These CD-based methods provide high-quality solutions to the complex non-convex layer-wise quantization problems. Notably, our CD-based approach features straightforward updates, relying solely on matrix and vector operations, circumventing the need for matrix inversion or decomposition. We also explore an outlier-aware variant of our approach, allowing for retaining significant weights (outliers) with complete precision. Our proposal attains state-of-the-art performance in terms of perplexity and zero-shot accuracy in empirical evaluations across various LLMs and datasets, with relative improvements up to 15% over methods such as GPTQ. Particularly noteworthy is our outlier-aware algorithm's capability to achieve near or sub-3-bit quantization of LLMs with an acceptable drop in accuracy, obviating the need for non-uniform quantization or grouping techniques, improving upon methods such as SpQR by up to two times in terms of perplexity.

mSAM: Micro-Batch-Averaged Sharpness-Aware Minimization

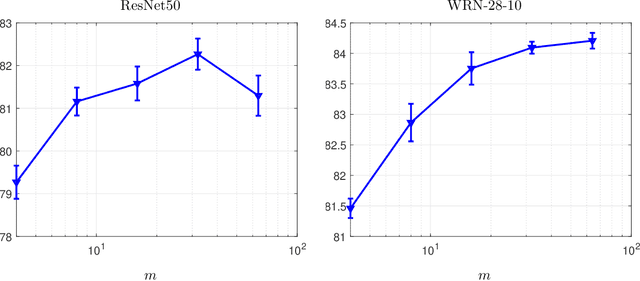
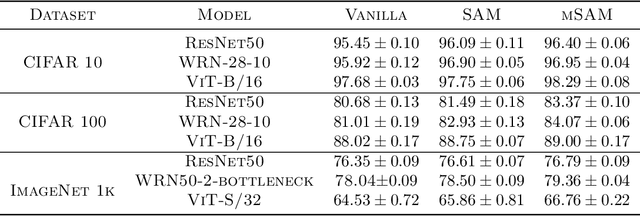
Modern deep learning models are over-parameterized, where different optima can result in widely varying generalization performance. To account for this, Sharpness-Aware Minimization (SAM) modifies the underlying loss function to guide descent methods towards flatter minima, which arguably have better generalization abilities. In this paper, we focus on a variant of SAM known as micro-batch SAM (mSAM), which, during training, averages the updates generated by adversarial perturbations across several disjoint shards (micro batches) of a mini-batch. We extend a recently developed and well-studied general framework for flatness analysis to show that distributed gradient computation for sharpness-aware minimization theoretically achieves even flatter minima. In order to support this theoretical superiority, we provide a thorough empirical evaluation on a variety of image classification and natural language processing tasks. We also show that contrary to previous work, mSAM can be implemented in a flexible and parallelizable manner without significantly increasing computational costs. Our practical implementation of mSAM yields superior generalization performance across a wide range of tasks compared to SAM, further supporting our theoretical framework.

Improved Deep Neural Network Generalization Using m-Sharpness-Aware Minimization

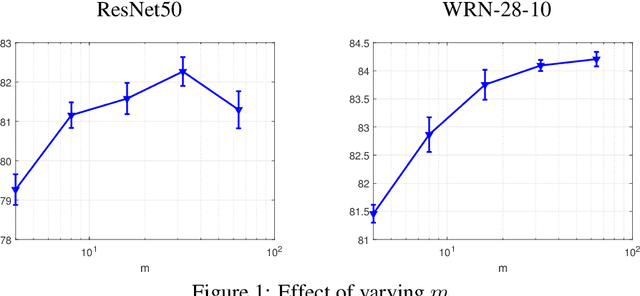
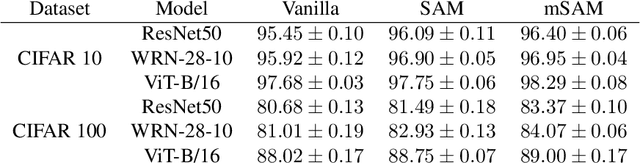
Modern deep learning models are over-parameterized, where the optimization setup strongly affects the generalization performance. A key element of reliable optimization for these systems is the modification of the loss function. Sharpness-Aware Minimization (SAM) modifies the underlying loss function to guide descent methods towards flatter minima, which arguably have better generalization abilities. In this paper, we focus on a variant of SAM known as mSAM, which, during training, averages the updates generated by adversarial perturbations across several disjoint shards of a mini-batch. Recent work suggests that mSAM can outperform SAM in terms of test accuracy. However, a comprehensive empirical study of mSAM is missing from the literature -- previous results have mostly been limited to specific architectures and datasets. To that end, this paper presents a thorough empirical evaluation of mSAM on various tasks and datasets. We provide a flexible implementation of mSAM and compare the generalization performance of mSAM to the performance of SAM and vanilla training on different image classification and natural language processing tasks. We also conduct careful experiments to understand the computational cost of training with mSAM, its sensitivity to hyperparameters and its correlation with the flatness of the loss landscape. Our analysis reveals that mSAM yields superior generalization performance and flatter minima, compared to SAM, across a wide range of tasks without significantly increasing computational costs.

Isometric Graph Neural Networks

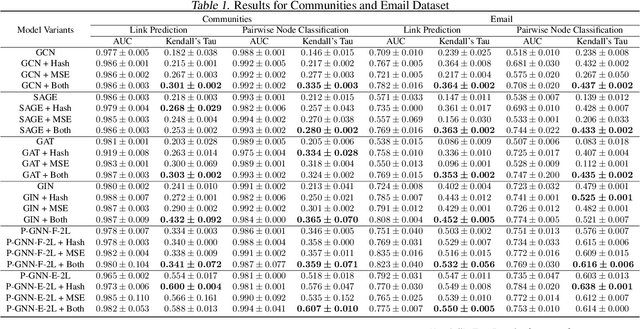
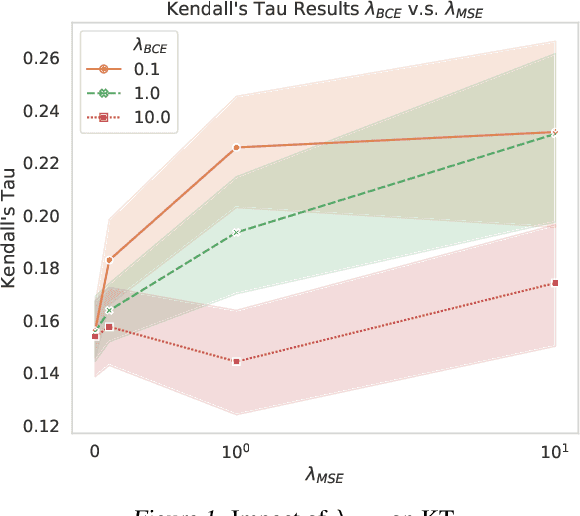
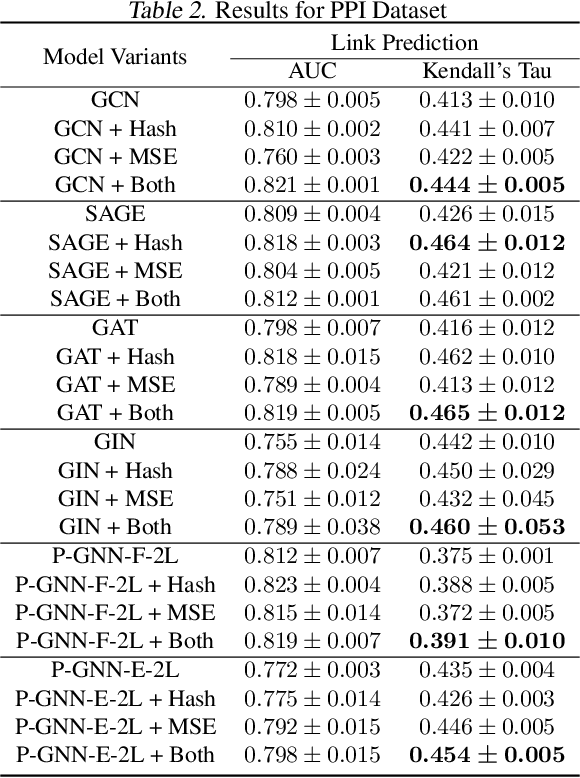
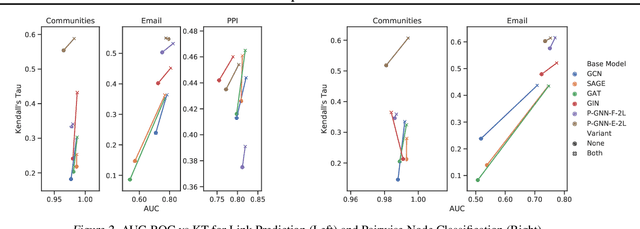
Many tasks that rely on representations of nodes in graphs would benefit if those representations were faithful to distances between nodes in the graph. Geometric techniques to extract such representations have poor scaling over large graph size, and recent advances in Graph Neural Network (GNN) algorithms have limited ability to reflect graph distance information beyond the first degree neighborhood. To enable this highly desired capability, we propose a technique to learn Isometric Graph Neural Networks (IGNN), which requires changing the input representation space and loss function to enable any GNN algorithm to generate representations that reflect distances between nodes. We experiment with the isometric technique on several GNN architectures for modeling multiple prediction tasks on multiple datasets. In addition to an improvement in AUC-ROC as high as $43\%$ in these experiments, we observe a consistent and substantial improvement as high as 400% in Kendall's Tau (KT), a measure that directly reflects distance information, demonstrating that the learned embeddings do account for graph distances.

Nonparametric Bayesian Factor Analysis for Dynamic Count Matrices

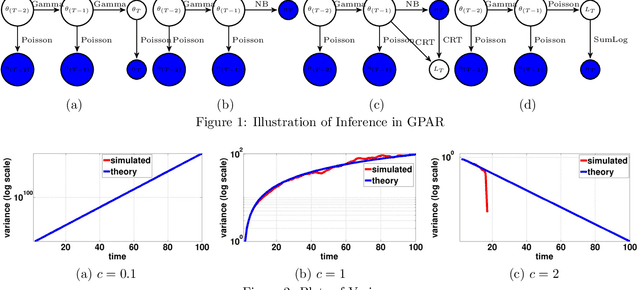
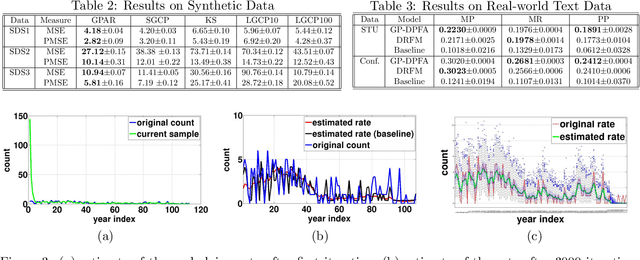
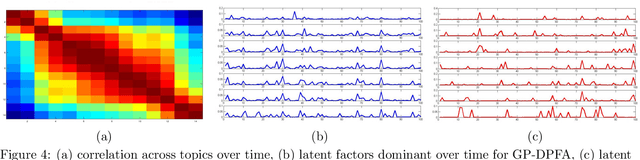
A gamma process dynamic Poisson factor analysis model is proposed to factorize a dynamic count matrix, whose columns are sequentially observed count vectors. The model builds a novel Markov chain that sends the latent gamma random variables at time $(t-1)$ as the shape parameters of those at time $t$, which are linked to observed or latent counts under the Poisson likelihood. The significant challenge of inferring the gamma shape parameters is fully addressed, using unique data augmentation and marginalization techniques for the negative binomial distribution. The same nonparametric Bayesian model also applies to the factorization of a dynamic binary matrix, via a Bernoulli-Poisson link that connects a binary observation to a latent count, with closed-form conditional posteriors for the latent counts and efficient computation for sparse observations. We apply the model to text and music analysis, with state-of-the-art results.

Probabilistic Combination of Classifier and Cluster Ensembles for Non-transductive Learning

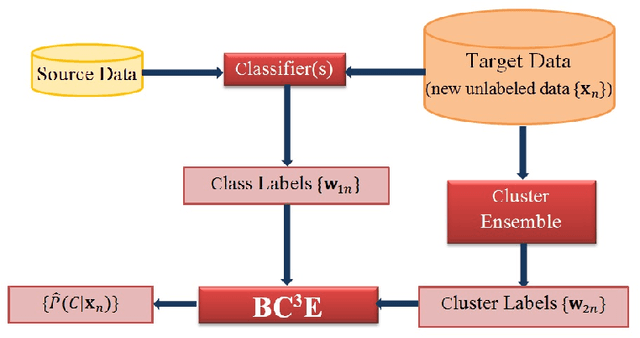
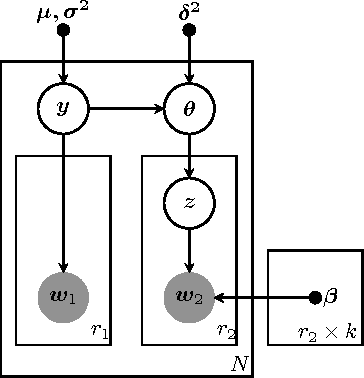
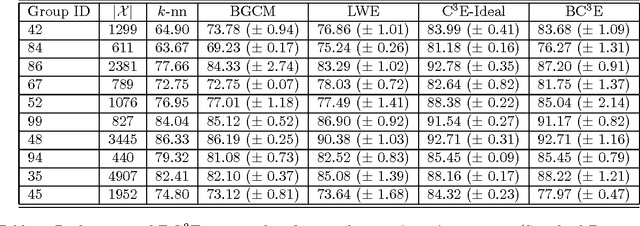
Unsupervised models can provide supplementary soft constraints to help classify new target data under the assumption that similar objects in the target set are more likely to share the same class label. Such models can also help detect possible differences between training and target distributions, which is useful in applications where concept drift may take place. This paper describes a Bayesian framework that takes as input class labels from existing classifiers (designed based on labeled data from the source domain), as well as cluster labels from a cluster ensemble operating solely on the target data to be classified, and yields a consensus labeling of the target data. This framework is particularly useful when the statistics of the target data drift or change from those of the training data. We also show that the proposed framework is privacy-aware and allows performing distributed learning when data/models have sharing restrictions. Experiments show that our framework can yield superior results to those provided by applying classifier ensembles only.

A Privacy-Aware Bayesian Approach for Combining Classifier and Cluster Ensembles

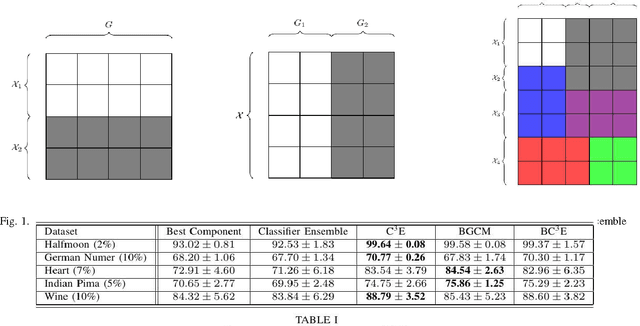
This paper introduces a privacy-aware Bayesian approach that combines ensembles of classifiers and clusterers to perform semi-supervised and transductive learning. We consider scenarios where instances and their classification/clustering results are distributed across different data sites and have sharing restrictions. As a special case, the privacy aware computation of the model when instances of the target data are distributed across different data sites, is also discussed. Experimental results show that the proposed approach can provide good classification accuracies while adhering to the data/model sharing constraints.

An Optimization Framework for Semi-Supervised and Transfer Learning using Multiple Classifiers and Clusterers

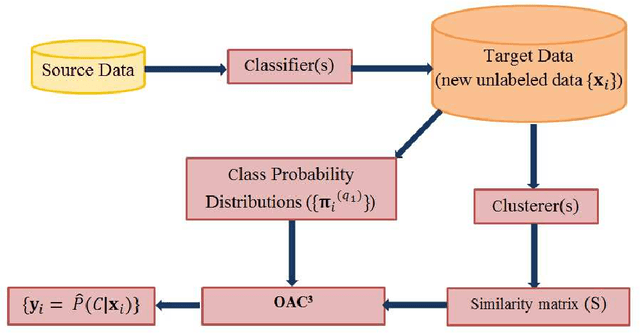
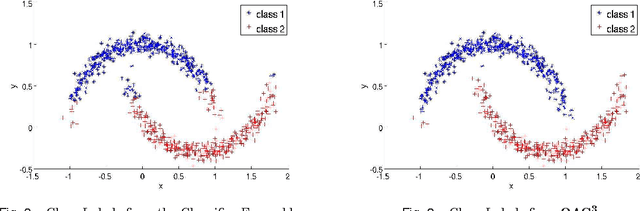
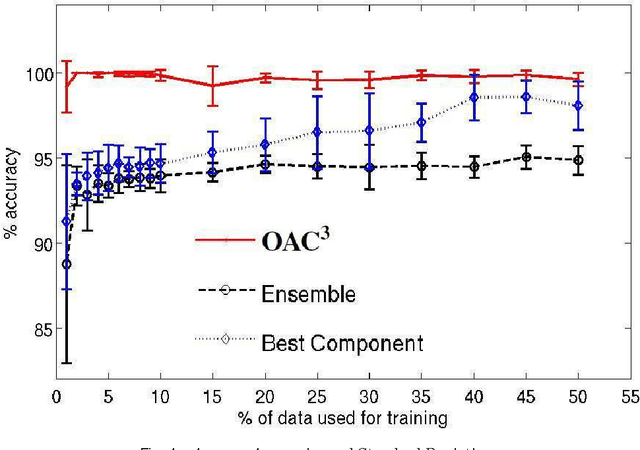
Unsupervised models can provide supplementary soft constraints to help classify new, "target" data since similar instances in the target set are more likely to share the same class label. Such models can also help detect possible differences between training and target distributions, which is useful in applications where concept drift may take place, as in transfer learning settings. This paper describes a general optimization framework that takes as input class membership estimates from existing classifiers learnt on previously encountered "source" data, as well as a similarity matrix from a cluster ensemble operating solely on the target data to be classified, and yields a consensus labeling of the target data. This framework admits a wide range of loss functions and classification/clustering methods. It exploits properties of Bregman divergences in conjunction with Legendre duality to yield a principled and scalable approach. A variety of experiments show that the proposed framework can yield results substantially superior to those provided by popular transductive learning techniques or by naively applying classifiers learnt on the original task to the target data.

Extension of Max-Min Ant System with Exponential Pheromone Deposition Rule

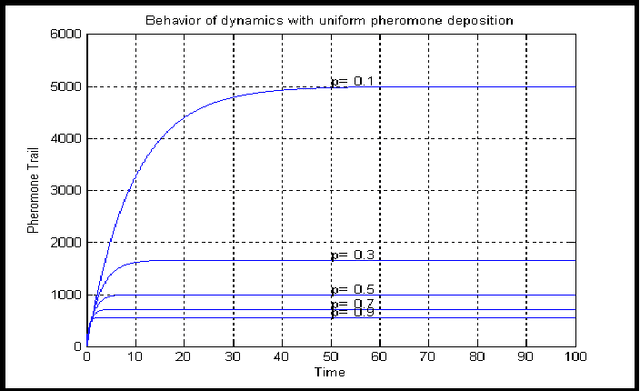
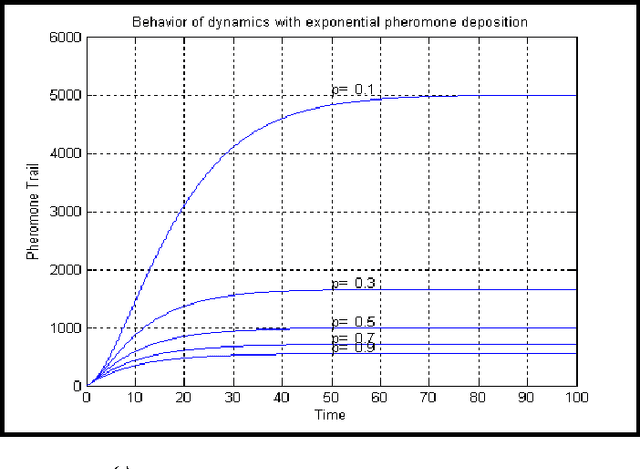
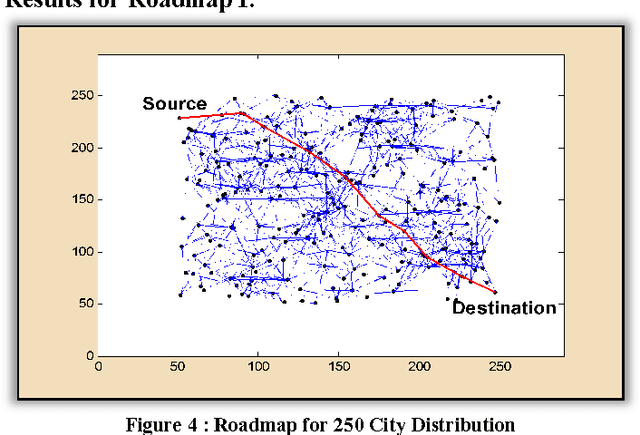
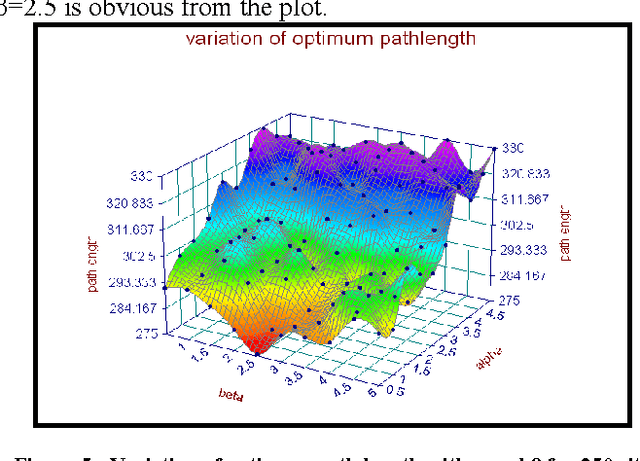
The paper presents an exponential pheromone deposition approach to improve the performance of classical Ant System algorithm which employs uniform deposition rule. A simplified analysis using differential equations is carried out to study the stability of basic ant system dynamics with both exponential and constant deposition rules. A roadmap of connected cities, where the shortest path between two specified cities are to be found out, is taken as a platform to compare Max-Min Ant System model (an improved and popular model of Ant System algorithm) with exponential and constant deposition rules. Extensive simulations are performed to find the best parameter settings for non-uniform deposition approach and experiments with these parameter settings revealed that the above approach outstripped the traditional one by a large extent in terms of both solution quality and convergence time.