Computation of Least Trimmed Squares: A Branch-and-Bound framework with Hyperplane Arrangement Enhancements

We study computational aspects of a key problem in robust statistics -- the penalized least trimmed squares (LTS) regression problem, a robust estimator that mitigates the influence of outliers in data by capping residuals with large magnitudes. Although statistically attractive, penalized LTS is NP-hard, and existing mixed-integer optimization (MIO) formulations scale poorly due to weak relaxations and exponential worst-case complexity in the number of observations. We propose a new MIO formulation that embeds hyperplane arrangement logic into a perspective reformulation, explicitly enforcing structural properties of optimal solutions. We show that, if the number of features is fixed, the resulting branch-and-bound tree is of polynomial size in the sample size. Moreover, we develop a tailored branch-and-bound algorithm that uses first-order methods with dual bounds to solve node relaxations efficiently. Computational experiments on synthetic and real datasets demonstrate substantial improvements over existing MIO approaches: on synthetic instances with 5000 samples and 20 features, our tailored solver reaches a 1% gap in 1 minute while competing approaches fail to do so within one hour. These gains enable exact robust regression at significantly larger sample sizes in low-dimensional settings.

MOONSHOT : A Framework for Multi-Objective Pruning of Vision and Large Language Models

Weight pruning is a common technique for compressing large neural networks. We focus on the challenging post-training one-shot setting, where a pre-trained model is compressed without any retraining. Existing one-shot pruning methods typically optimize a single objective, such as a layer-wise reconstruction loss or a second-order Taylor approximation of the training loss. We highlight that neither objective alone is consistently the most effective across architectures and sparsity levels. Motivated by this insight, we propose MOONSHOT, a general and flexible framework that extends any single-objective pruning method into a multi-objective formulation by jointly optimizing both the layer-wise reconstruction error and second-order Taylor approximation of the training loss. MOONSHOT acts as a wrapper around existing pruning algorithms. To enable this integration while maintaining scalability to billion-parameter models, we propose modeling decisions and introduce an efficient procedure for computing the inverse Hessian, preserving the efficiency of state-of-the-art one-shot pruners. When combined with state-of-the-art pruning methods on Llama-3.2 and Llama-2 models, MOONSHOT reduces C4 perplexity by up to 32.6% at 2:4 sparsity and improves zero-shot mean accuracy across seven classification benchmarks by up to 4.9 points. On Vision Transformers, it improves accuracy on ImageNet-1k by over 5 points at 70% sparsity, and on ResNet-50, it yields a 4-point gain at 90% sparsity.

Robust Batch-Level Query Routing for Large Language Models under Cost and Capacity Constraints

We study the problem of routing queries to large language models (LLMs) under cost, GPU resources, and concurrency constraints. Prior per-query routing methods often fail to control batch-level cost, especially under non-uniform or adversarial batching. To address this, we propose a batch-level, resource-aware routing framework that jointly optimizes model assignment for each batch while respecting cost and model capacity limits. We further introduce a robust variant that accounts for uncertainty in predicted LLM performance, along with an offline instance allocation procedure that balances quality and throughput across multiple models. Experiments on two multi-task LLM benchmarks show that robustness improves accuracy by 1-14% over non-robust counterparts (depending on the performance estimator), batch-level routing outperforms per-query methods by up to 24% under adversarial batching, and optimized instance allocation yields additional gains of up to 3% compared to a non-optimized allocation, all while strictly controlling cost and GPU resource constraints.

3BASiL: An Algorithmic Framework for Sparse plus Low-Rank Compression of LLMs

Sparse plus Low-Rank $(\mathbf{S} + \mathbf{LR})$ decomposition of Large Language Models (LLMs) has emerged as a promising direction in model compression, aiming to decompose pre-trained model weights into a sum of sparse and low-rank matrices $(\mathbf{W} \approx \mathbf{S} + \mathbf{LR})$. Despite recent progress, existing methods often suffer from substantial performance degradation compared to dense models. In this work, we introduce 3BASiL-TM, an efficient one-shot post-training method for $(\mathbf{S} + \mathbf{LR})$ decomposition of LLMs that addresses this gap. Our approach first introduces a novel 3-Block Alternating Direction Method of Multipliers (ADMM) method, termed 3BASiL, to minimize the layer-wise reconstruction error with convergence guarantees. We then design an efficient transformer-matching (TM) refinement step that jointly optimizes the sparse and low-rank components across transformer layers. This step minimizes a novel memory-efficient loss that aligns outputs at the transformer level. Notably, the TM procedure is universal as it can enhance any $(\mathbf{S} + \mathbf{LR})$ decomposition, including pure sparsity. Our numerical experiments show that 3BASiL-TM reduces the WikiText2 perplexity gap relative to dense LLaMA-8B model by over 30% under a (2:4 Sparse + 64 LR) configuration, compared to prior methods. Moreover, our method achieves over 2.5x faster compression runtime on an A100 GPU compared to SOTA $(\mathbf{S} + \mathbf{LR})$ method. Our code is available at https://github.com/mazumder-lab/3BASiL.

Reasoning Models Can be Accurately Pruned Via Chain-of-Thought Reconstruction

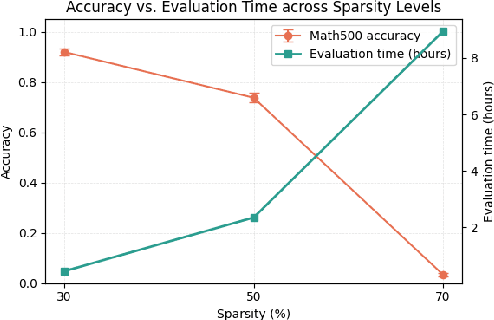
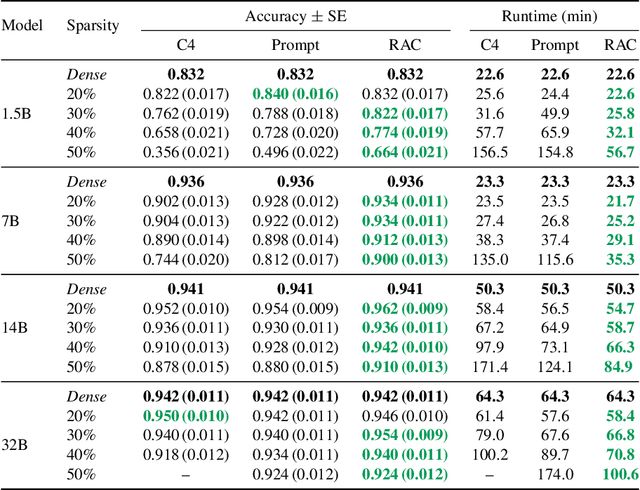
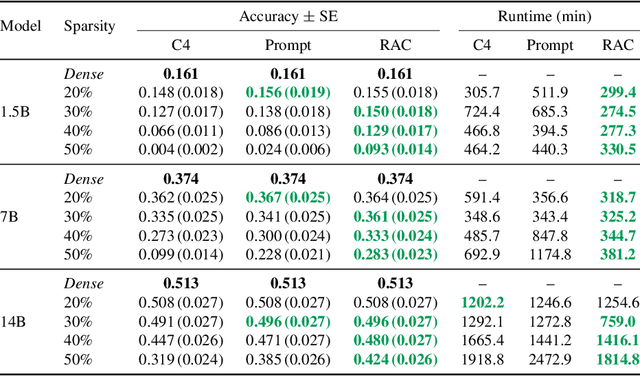
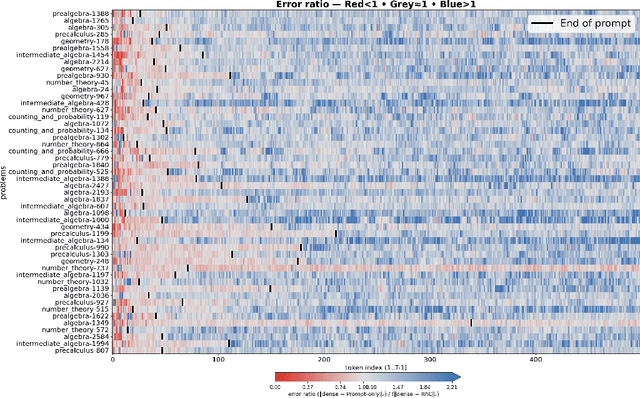
Reasoning language models such as DeepSeek-R1 produce long chain-of-thought traces during inference time which make them costly to deploy at scale. We show that using compression techniques such as neural network pruning produces greater performance loss than in typical language modeling tasks, and in some cases can make the model slower since they cause the model to produce more thinking tokens but with worse performance. We show that this is partly due to the fact that standard LLM pruning methods often focus on input reconstruction, whereas reasoning is a decode-dominated task. We introduce a simple, drop-in fix: during pruning we jointly reconstruct activations from the input and the model's on-policy chain-of-thought traces. This "Reasoning-Aware Compression" (RAC) integrates seamlessly into existing pruning workflows such as SparseGPT, and boosts their performance significantly. Code reproducing the results in the paper can be found at: https://github.com/RyanLucas3/RAC

TSENOR: Highly-Efficient Algorithm for Finding Transposable N:M Sparse Masks

Network pruning reduces the computational requirements of large neural networks, with N:M sparsity -- retaining only N out of every M consecutive weights -- offering a compelling balance between compressed model quality and hardware acceleration. However, N:M sparsity only accelerates forward-pass computations, as N:M patterns are not preserved during matrix transposition, limiting efficiency during training where both passes are computationally intensive. While transposable N:M sparsity has been proposed to address this limitation, existing methods for finding transposable N:M sparse masks either fail to scale to large models or are restricted to M=4 which results in suboptimal compression-accuracy trade-off. We introduce an efficient solver for transposable N:M masks that scales to billion-parameter models. We formulate mask generation as optimal transport problems and solve through entropy regularization and Dykstra's algorithm, followed by a rounding procedure. Our tensor-based implementation exploits GPU parallelism, achieving up to 100x speedup with only 1-10% error compared to existing methods. Our approach can be integrated with layer-wise N:M pruning frameworks including Wanda, SparseGPT and ALPS to produce transposable N:M sparse models with arbitrary N:M values. Experiments show that LLaMA3.2-8B with transposable 16:32 sparsity maintains performance close to its standard N:M counterpart and outperforms standard 2:4 sparse model, showing the practical value of our approach.

An Optimization Framework for Differentially Private Sparse Fine-Tuning

Differentially private stochastic gradient descent (DP-SGD) is broadly considered to be the gold standard for training and fine-tuning neural networks under differential privacy (DP). With the increasing availability of high-quality pre-trained model checkpoints (e.g., vision and language models), fine-tuning has become a popular strategy. However, despite recent progress in understanding and applying DP-SGD for private transfer learning tasks, significant challenges remain -- most notably, the performance gap between models fine-tuned with DP-SGD and their non-private counterparts. Sparse fine-tuning on private data has emerged as an alternative to full-model fine-tuning; recent work has shown that privately fine-tuning only a small subset of model weights and keeping the rest of the weights fixed can lead to better performance. In this work, we propose a new approach for sparse fine-tuning of neural networks under DP. Existing work on private sparse finetuning often used fixed choice of trainable weights (e.g., updating only the last layer), or relied on public model's weights to choose the subset of weights to modify. Such choice of weights remains suboptimal. In contrast, we explore an optimization-based approach, where our selection method makes use of the private gradient information, while using off the shelf privacy accounting techniques. Our numerical experiments on several computer vision models and datasets show that our selection method leads to better prediction accuracy, compared to full-model private fine-tuning or existing private sparse fine-tuning approaches.

Efficient AI in Practice: Training and Deployment of Efficient LLMs for Industry Applications

Large language models (LLMs) have demonstrated remarkable performance across a wide range of industrial applications, from search and recommendations to generative tasks. Although scaling laws indicate that larger models generally yield better generalization and performance, their substantial computational requirements often render them impractical for many real-world scenarios at scale. In this paper, we present methods and insights for training small language models (SLMs) that deliver high performance and efficiency in deployment. We focus on two key techniques: (1) knowledge distillation and (2) model compression via quantization and pruning. These approaches enable SLMs to retain much of the quality of their larger counterparts while significantly reducing training, serving costs, and latency. We detail the impact of these techniques on a variety of use cases at a large professional social network platform and share deployment lessons - including hardware optimization strategies that enhance speed and throughput for both predictive and reasoning-based applications.

HASSLE-free: A unified Framework for Sparse plus Low-Rank Matrix Decomposition for LLMs

The impressive capabilities of large foundation models come at a cost of substantial computing resources to serve them. Compressing these pre-trained models is of practical interest as it can democratize deploying them to the machine learning community at large by lowering the costs associated with inference. A promising compression scheme is to decompose foundation models' dense weights into a sum of sparse plus low-rank matrices. In this paper, we design a unified framework coined HASSLE-free for (semi-structured) sparse plus low-rank matrix decomposition of foundation models. Our framework introduces the local layer-wise reconstruction error objective for this decomposition, we demonstrate that prior work solves a relaxation of this optimization problem; and we provide efficient and scalable methods to minimize the exact introduced optimization problem. HASSLE-free substantially outperforms state-of-the-art methods in terms of the introduced objective and a wide range of LLM evaluation benchmarks. For the Llama3-8B model with a 2:4 sparsity component plus a 64-rank component decomposition, a compression scheme for which recent work shows important inference acceleration on GPUs, HASSLE-free reduces the test perplexity by 12% for the WikiText-2 dataset and reduces the gap (compared to the dense model) of the average of eight popular zero-shot tasks by 15% compared to existing methods.

Efficient user history modeling with amortized inference for deep learning recommendation models

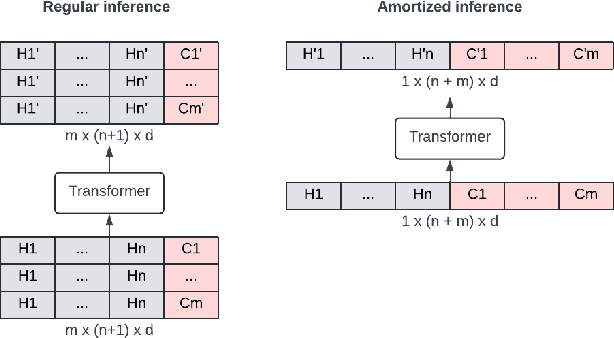
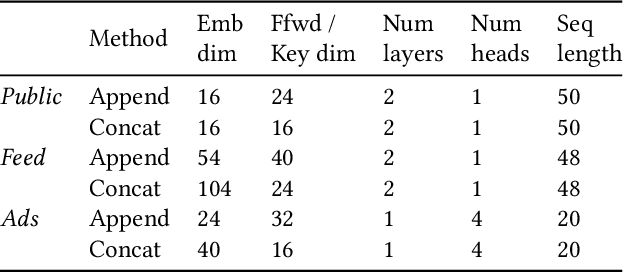
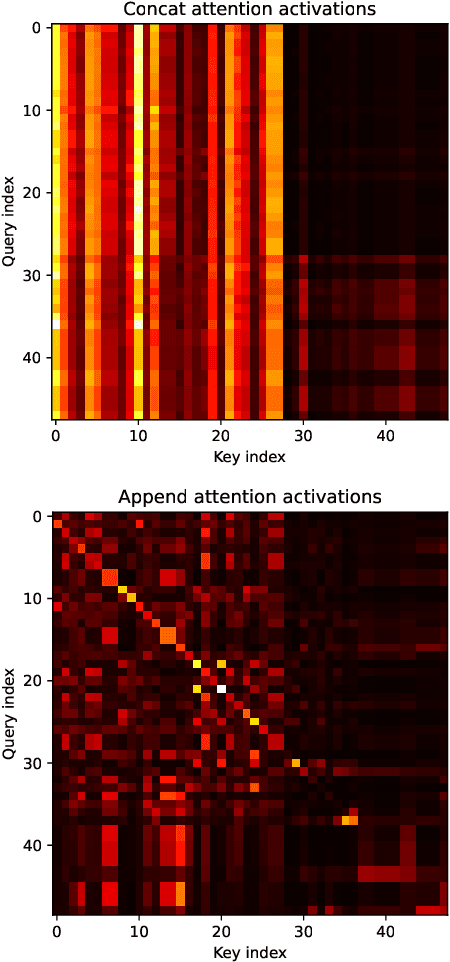
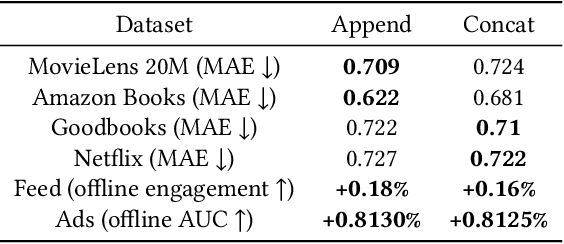
We study user history modeling via Transformer encoders in deep learning recommendation models (DLRM). Such architectures can significantly improve recommendation quality, but usually incur high latency cost necessitating infrastructure upgrades or very small Transformer models. An important part of user history modeling is early fusion of the candidate item and various methods have been studied. We revisit early fusion and compare concatenation of the candidate to each history item against appending it to the end of the list as a separate item. Using the latter method, allows us to reformulate the recently proposed amortized history inference algorithm M-FALCON \cite{zhai2024actions} for the case of DLRM models. We show via experimental results that appending with cross-attention performs on par with concatenation and that amortization significantly reduces inference costs. We conclude with results from deploying this model on the LinkedIn Feed and Ads surfaces, where amortization reduces latency by 30\% compared to non-amortized inference.