OTPrune: Distribution-Aligned Visual Token Pruning via Optimal Transport

Multi-modal large language models (MLLMs) achieve strong visual-language reasoning but suffer from high inference cost due to redundant visual tokens. Recent work explores visual token pruning to accelerate inference, while existing pruning methods overlook the underlying distributional structure of visual representations. We propose OTPrune, a training-free framework that formulates pruning as distribution alignment via optimal transport (OT). By minimizing the 2-Wasserstein distance between the full and pruned token distributions, OTPrune preserves both local diversity and global representativeness while reducing inference cost. Moreover, we derive a tractable submodular objective that enables efficient optimization, and theoretically prove its monotonicity and submodularity, providing a principled foundation for stable and efficient pruning. We further provide a comprehensive analysis that explains how distributional alignment contributes to stable and semantically faithful pruning. Comprehensive experiments on wider benchmarks demonstrate that OTPrune achieves superior performance-efficiency tradeoffs compared to state-of-the-art methods. The code is available at https://github.com/xiwenc1/OTPrune.

Bayesian Preference Learning for Test-Time Steerable Reward Models

Reward models are central to aligning language models with human preferences via reinforcement learning (RL). As RL is increasingly applied to settings such as verifiable rewards and multi-objective alignment, RMs are expected to encode more complex and multifaceted preference distributions. However, classifier RMs remain static once trained, limiting their adaptability at test time. We propose Variational In-Context Reward Modeling (ICRM), a novel Bayesian reward modeling objective that enables test-time steerability via in-context preference demonstrations. ICRM casts reward modeling as amortized variational inference over a latent preference probability under the Bradley-Terry model using a conjugate Beta prior. We show that ICRM adapt to unseen preference distributions at test time for both single and multi-objective settings. With more in-context demonstrations, ICRM gains 34% accuracy on SafeRLHF and 9% accuracy on RM-Bench in the single-objective setting, while widening the Pareto frontier with a 4% gain in hypervolume on helpfulness and refusal benchmarks. We further study the practical applicability of ICRM for RL training, showing that it can effectively encode verifiable rewards by outperforming a conventional RM in math reasoning. Finally, we provide theoretical guarantees that the variational objective admits a global interior optimum with finite confidence, and we analyze how KL regularization mitigates reward over-optimization.

Distilling the Essence: Efficient Reasoning Distillation via Sequence Truncation

Distilling the reasoning capabilities from a large language model (LLM) to a smaller student model often involves training on substantial amounts of reasoning data. However, distillation over lengthy sequences with prompt (P), chain-of-thought (CoT), and answer (A) segments makes the process computationally expensive. In this work, we investigate how the allocation of supervision across different segments (P, CoT, A) affects student performance. Our analysis shows that selective knowledge distillation over only the CoT tokens can be effective when the prompt and answer information is encompassed by it. Building on this insight, we establish a truncation protocol to quantify computation-quality tradeoffs as a function of sequence length. We observe that training on only the first $50\%$ of tokens of every training sequence can retain, on average, $\approx94\%$ of full-sequence performance on math benchmarks while reducing training time, memory usage, and FLOPs by about $50\%$ each. These findings suggest that reasoning distillation benefits from prioritizing early reasoning tokens and provides a simple lever for computation-quality tradeoffs. Codes are available at https://github.com/weiruichen01/distilling-the-essence.

Reasoning Models Can be Accurately Pruned Via Chain-of-Thought Reconstruction

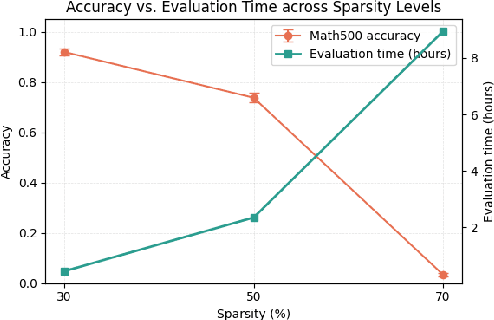
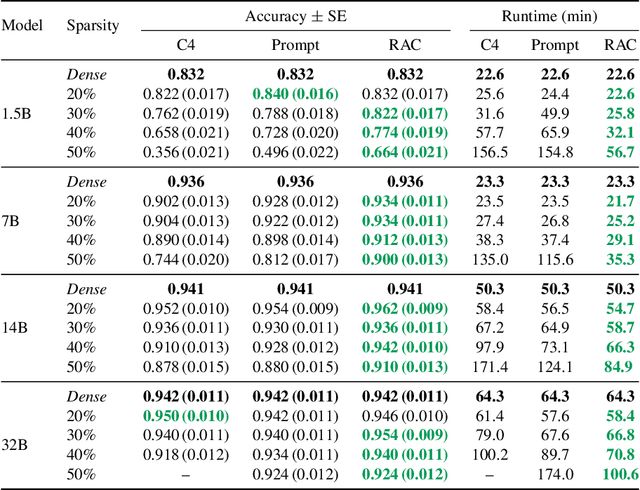
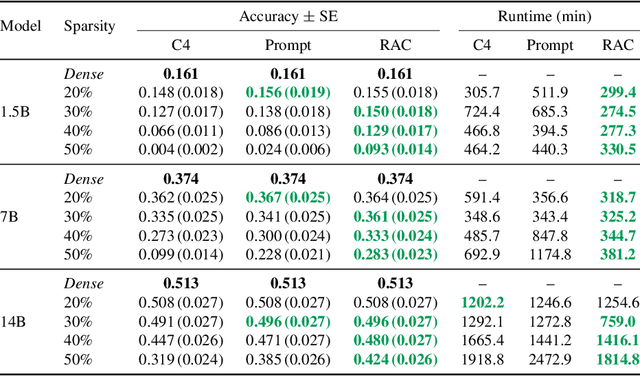
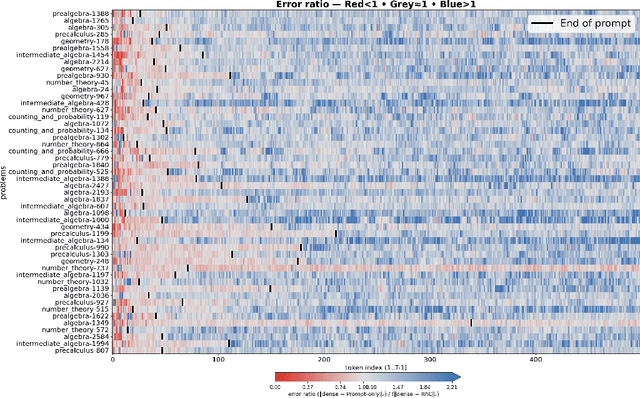
Reasoning language models such as DeepSeek-R1 produce long chain-of-thought traces during inference time which make them costly to deploy at scale. We show that using compression techniques such as neural network pruning produces greater performance loss than in typical language modeling tasks, and in some cases can make the model slower since they cause the model to produce more thinking tokens but with worse performance. We show that this is partly due to the fact that standard LLM pruning methods often focus on input reconstruction, whereas reasoning is a decode-dominated task. We introduce a simple, drop-in fix: during pruning we jointly reconstruct activations from the input and the model's on-policy chain-of-thought traces. This "Reasoning-Aware Compression" (RAC) integrates seamlessly into existing pruning workflows such as SparseGPT, and boosts their performance significantly. Code reproducing the results in the paper can be found at: https://github.com/RyanLucas3/RAC

LiDDA: Data Driven Attribution at LinkedIn

Data Driven Attribution, which assigns conversion credits to marketing interactions based on causal patterns learned from data, is the foundation of modern marketing intelligence and vital to any marketing businesses and advertising platform. In this paper, we introduce a unified transformer-based attribution approach that can handle member-level data, aggregate-level data, and integration of external macro factors. We detail the large scale implementation of the approach at LinkedIn, showcasing significant impact. We also share learning and insights that are broadly applicable to the marketing and ad tech fields.

On the Robustness of Reward Models for Language Model Alignment

The Bradley-Terry (BT) model is widely practiced in reward modeling for reinforcement learning with human feedback (RLHF). Despite its effectiveness, reward models (RMs) trained with BT model loss are prone to over-optimization, losing generalizability to unseen input distributions. In this paper, we study the cause of over-optimization in RM training and its downstream effects on the RLHF procedure, accentuating the importance of distributional robustness of RMs in unseen data. First, we show that the excessive dispersion of hidden state norms is the main source of over-optimization. Then, we propose batch-wise sum-to-zero regularization (BSR) to enforce zero-centered reward sum per batch, constraining the rewards with extreme magnitudes. We assess the impact of BSR in improving robustness in RMs through four scenarios of over-optimization, where BSR consistently manifests better robustness. Subsequently, we compare the plain BT model and BSR on RLHF training and empirically show that robust RMs better align the policy to the gold preference model. Finally, we apply BSR to high-quality data and models, which surpasses state-of-the-art RMs in the 8B scale by adding more than 5% in complex preference prediction tasks. By conducting RLOO training with 8B RMs, AlpacaEval 2.0 reduces generation length by 40% while adding a 7% increase in win rate, further highlighting that robustness in RMs induces robustness in RLHF training. We release the code, data, and models: https://github.com/LinkedIn-XFACT/RM-Robustness.

Efficient AI in Practice: Training and Deployment of Efficient LLMs for Industry Applications

Large language models (LLMs) have demonstrated remarkable performance across a wide range of industrial applications, from search and recommendations to generative tasks. Although scaling laws indicate that larger models generally yield better generalization and performance, their substantial computational requirements often render them impractical for many real-world scenarios at scale. In this paper, we present methods and insights for training small language models (SLMs) that deliver high performance and efficiency in deployment. We focus on two key techniques: (1) knowledge distillation and (2) model compression via quantization and pruning. These approaches enable SLMs to retain much of the quality of their larger counterparts while significantly reducing training, serving costs, and latency. We detail the impact of these techniques on a variety of use cases at a large professional social network platform and share deployment lessons - including hardware optimization strategies that enhance speed and throughput for both predictive and reasoning-based applications.

From Features to Transformers: Redefining Ranking for Scalable Impact

We present LiGR, a large-scale ranking framework developed at LinkedIn that brings state-of-the-art transformer-based modeling architectures into production. We introduce a modified transformer architecture that incorporates learned normalization and simultaneous set-wise attention to user history and ranked items. This architecture enables several breakthrough achievements, including: (1) the deprecation of most manually designed feature engineering, outperforming the prior state-of-the-art system using only few features (compared to hundreds in the baseline), (2) validation of the scaling law for ranking systems, showing improved performance with larger models, more training data, and longer context sequences, and (3) simultaneous joint scoring of items in a set-wise manner, leading to automated improvements in diversity. To enable efficient serving of large ranking models, we describe techniques to scale inference effectively using single-pass processing of user history and set-wise attention. We also summarize key insights from various ablation studies and A/B tests, highlighting the most impactful technical approaches.

AlphaPO -- Reward shape matters for LLM alignment

Reinforcement Learning with Human Feedback (RLHF) and its variants have made huge strides toward the effective alignment of large language models (LLMs) to follow instructions and reflect human values. More recently, Direct Alignment Algorithms (DAAs) have emerged in which the reward modeling stage of RLHF is skipped by characterizing the reward directly as a function of the policy being learned. Examples include Direct Preference Optimization (DPO) and Simple Preference Optimization (SimPO). These methods often suffer from likelihood displacement, a phenomenon by which the probabilities of preferred responses are often reduced undesirably. In this paper, we argue that, for DAAs the reward (function) shape matters. We introduce AlphaPO, a new DAA method that leverages an $\alpha$-parameter to help change the shape of the reward function beyond the standard log reward. AlphaPO helps maintain fine-grained control over likelihood displacement and over-optimization. Compared to SimPO, one of the best performing DAAs, AlphaPO leads to about 7\% to 10\% relative improvement in alignment performance for the instruct versions of Mistral-7B and Llama3-8B. The analysis and results presented highlight the importance of the reward shape, and how one can systematically change it to affect training dynamics, as well as improve alignment performance.

Liger Kernel: Efficient Triton Kernels for LLM Training

Training Large Language Models (LLMs) efficiently at scale presents a formidable challenge, driven by their ever-increasing computational demands and the need for enhanced performance. In this work, we introduce Liger-Kernel, an open-sourced set of Triton kernels developed specifically for LLM training. With kernel optimization techniques like kernel operation fusing and input chunking, our kernels achieve on average a 20% increase in training throughput and a 60% reduction in GPU memory usage for popular LLMs compared to HuggingFace implementations. In addition, Liger-Kernel is designed with modularity, accessibility, and adaptability in mind, catering to both casual and expert users. Comprehensive benchmarks and integration tests are built in to ensure compatibility, performance, correctness, and convergence across diverse computing environments and model architectures. The source code is available under a permissive license at: github.com/linkedin/Liger-Kernel.