Mind the Jumps: A Scalable Robust Local Gaussian Process for Multidimensional Response Surfaces with Discontinuities

Modeling response surfaces with abrupt jumps and discontinuities remains a major challenge across scientific and engineering domains. Although Gaussian process models excel at capturing smooth nonlinear relationships, their stationarity assumptions limit their ability to adapt to sudden input-output variations. Existing nonstationary extensions, particularly those based on domain partitioning, often struggle with boundary inconsistencies, sensitivity to outliers, and scalability issues in higher-dimensional settings, leading to reduced predictive accuracy and unreliable parameter estimation. To address these challenges, this paper proposes the Robust Local Gaussian Process (RLGP) model, a framework that integrates adaptive nearest-neighbor selection with a sparsity-driven robustification mechanism. Unlike existing methods, RLGP leverages an optimization-based mean-shift adjustment after a multivariate perspective transformation combined with local neighborhood modeling to mitigate the influence of outliers. This approach improves predictive accuracy near discontinuities while enhancing robustness to data heterogeneity. Comprehensive evaluations on real-world datasets show that RLGP consistently delivers high predictive accuracy and maintains competitive computational efficiency, especially in scenarios with sharp transitions and complex response structures. Scalability tests further confirm RLGP's stability and reliability in higher-dimensional settings, where other methods struggle. These results establish RLGP as an effective and practical solution for modeling nonstationary and discontinuous response surfaces across a wide range of applications.

Slow Kill for Big Data Learning

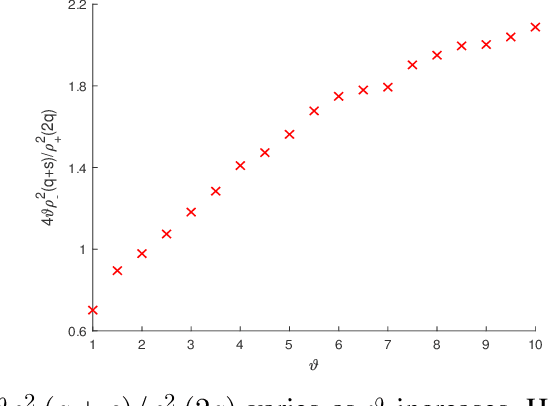
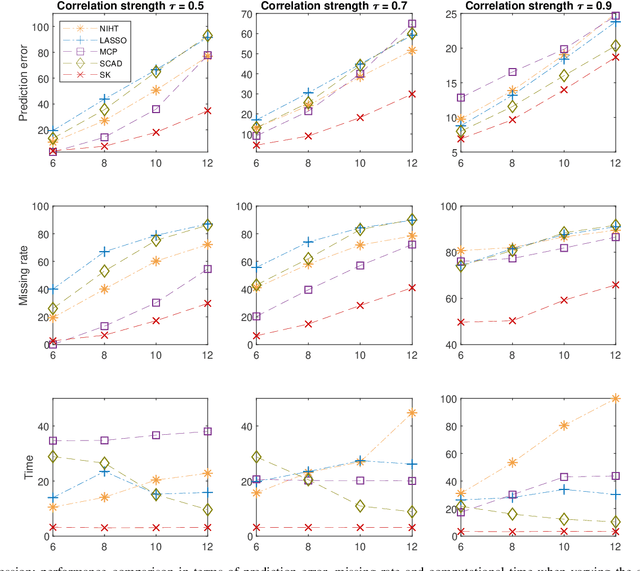
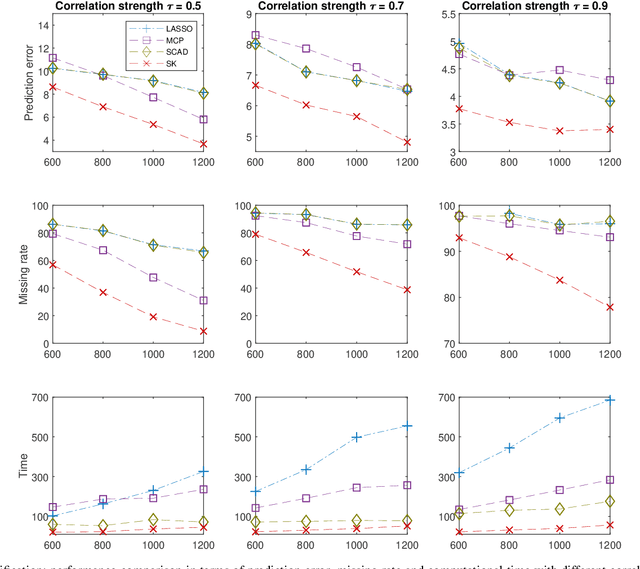
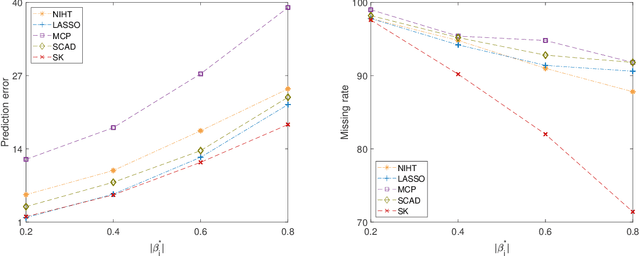
Big-data applications often involve a vast number of observations and features, creating new challenges for variable selection and parameter estimation. This paper presents a novel technique called ``slow kill,'' which utilizes nonconvex constrained optimization, adaptive $\ell_2$-shrinkage, and increasing learning rates. The fact that the problem size can decrease during the slow kill iterations makes it particularly effective for large-scale variable screening. The interaction between statistics and optimization provides valuable insights into controlling quantiles, stepsize, and shrinkage parameters in order to relax the regularity conditions required to achieve the desired level of statistical accuracy. Experimental results on real and synthetic data show that slow kill outperforms state-of-the-art algorithms in various situations while being computationally efficient for large-scale data.

Supervised Multivariate Learning with Simultaneous Feature Auto-grouping and Dimension Reduction

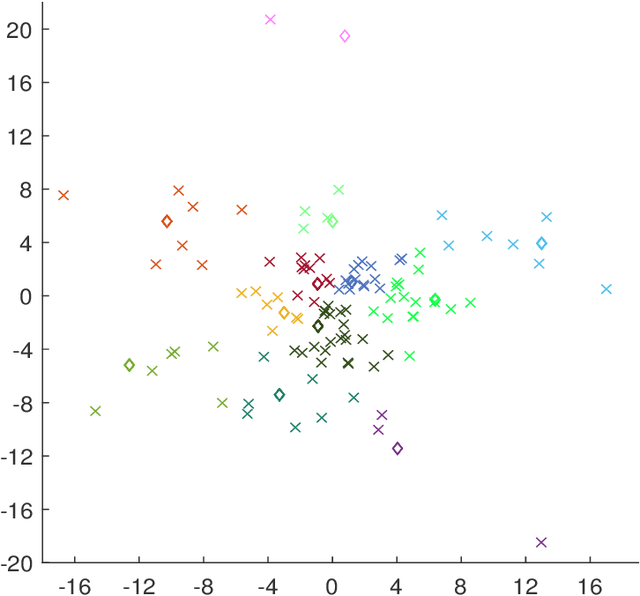
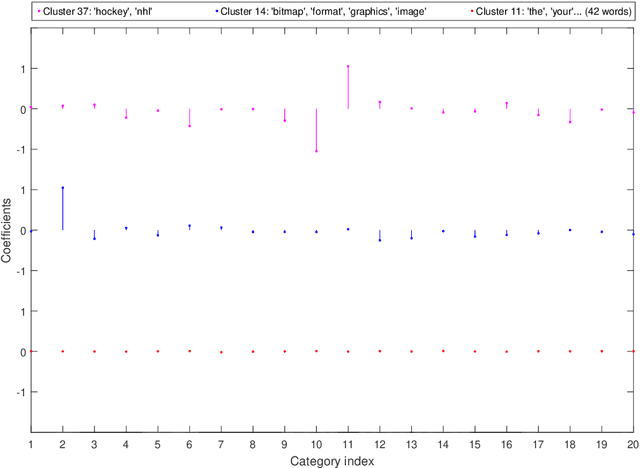
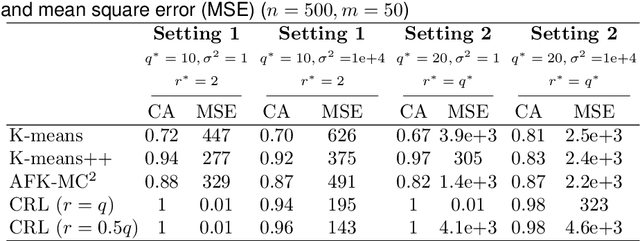
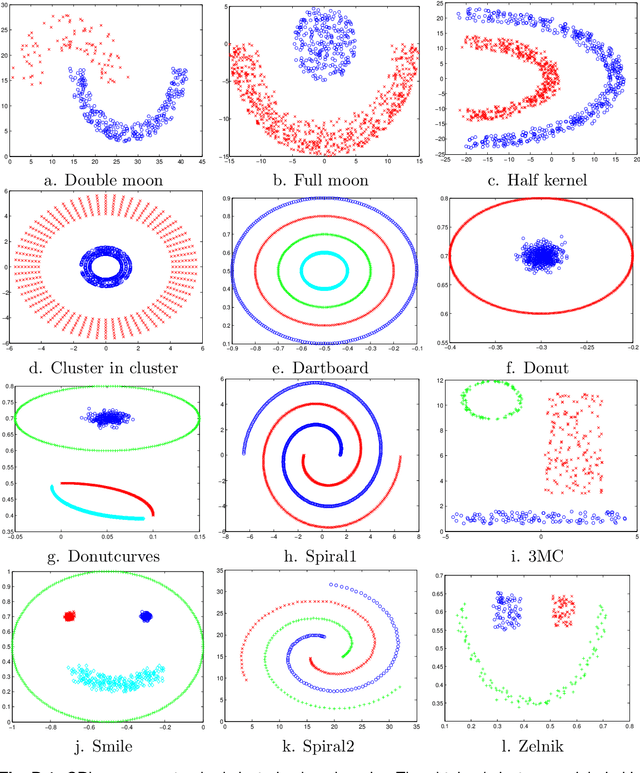
Modern high-dimensional methods often adopt the ``bet on sparsity'' principle, while in supervised multivariate learning statisticians may face ``dense'' problems with a large number of nonzero coefficients. This paper proposes a novel clustered reduced-rank learning (CRL) framework that imposes two joint matrix regularizations to automatically group the features in constructing predictive factors. CRL is more interpretable than low-rank modeling and relaxes the stringent sparsity assumption in variable selection. In this paper, new information-theoretical limits are presented to reveal the intrinsic cost of seeking for clusters, as well as the blessing from dimensionality in multivariate learning. Moreover, an efficient optimization algorithm is developed, which performs subspace learning and clustering with guaranteed convergence. The obtained fixed-point estimators, though not necessarily globally optimal, enjoy the desired statistical accuracy beyond the standard likelihood setup under some regularity conditions. Moreover, a new kind of information criterion, as well as its scale-free form, is proposed for cluster and rank selection, and has a rigorous theoretical support without assuming an infinite sample size. Extensive simulations and real-data experiments demonstrate the statistical accuracy and interpretability of the proposed method.

Analysis of Generalized Bregman Surrogate Algorithms for Nonsmooth Nonconvex Statistical Learning

Modern statistical applications often involve minimizing an objective function that may be nonsmooth and/or nonconvex. This paper focuses on a broad Bregman-surrogate algorithm framework including the local linear approximation, mirror descent, iterative thresholding, DC programming and many others as particular instances. The recharacterization via generalized Bregman functions enables us to construct suitable error measures and establish global convergence rates for nonconvex and nonsmooth objectives in possibly high dimensions. For sparse learning problems with a composite objective, under some regularity conditions, the obtained estimators as the surrogate's fixed points, though not necessarily local minimizers, enjoy provable statistical guarantees, and the sequence of iterates can be shown to approach the statistical truth within the desired accuracy geometrically fast. The paper also studies how to design adaptive momentum based accelerations without assuming convexity or smoothness by carefully controlling stepsize and relaxation parameters.

Gaining Outlier Resistance with Progressive Quantiles: Fast Algorithms and Theoretical Studies

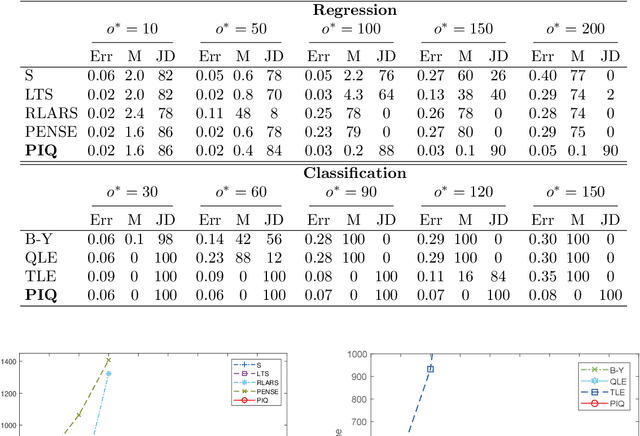
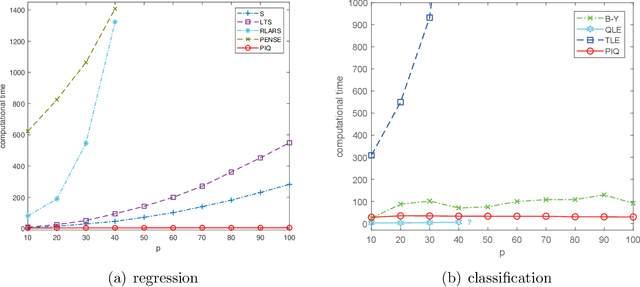
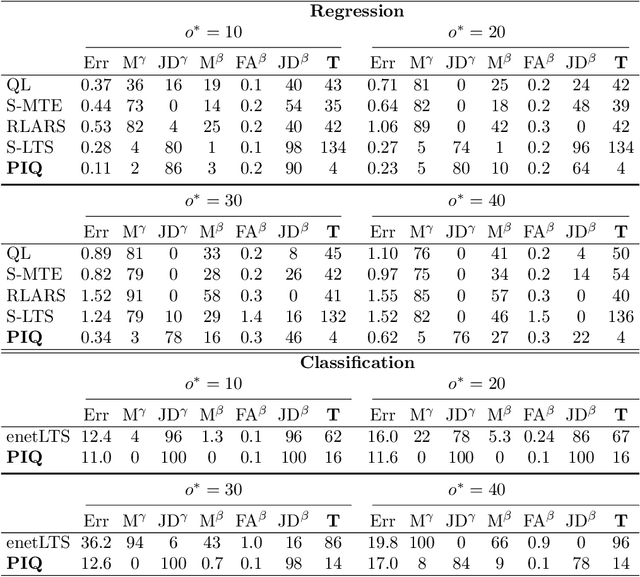
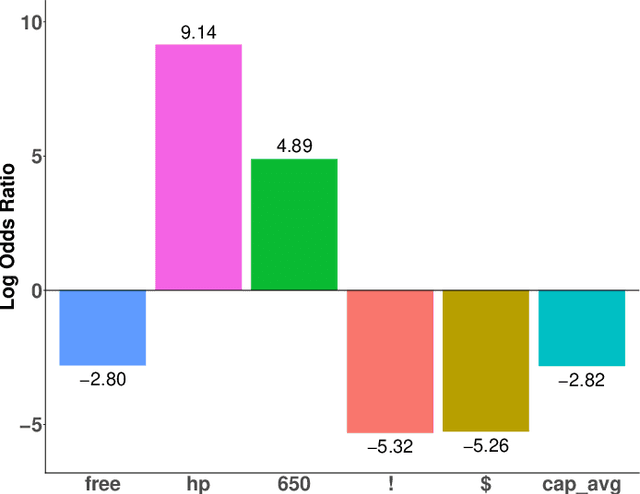
Outliers widely occur in big-data applications and may severely affect statistical estimation and inference. In this paper, a framework of outlier-resistant estimation is introduced to robustify an arbitrarily given loss function. It has a close connection to the method of trimming and includes explicit outlyingness parameters for all samples, which in turn facilitates computation, theory, and parameter tuning. To tackle the issues of nonconvexity and nonsmoothness, we develop scalable algorithms with implementation ease and guaranteed fast convergence. In particular, a new technique is proposed to alleviate the requirement on the starting point such that on regular datasets, the number of data resamplings can be substantially reduced. Based on combined statistical and computational treatments, we are able to perform nonasymptotic analysis beyond M-estimation. The obtained resistant estimators, though not necessarily globally or even locally optimal, enjoy minimax rate optimality in both low dimensions and high dimensions. Experiments in regression, classification, and neural networks show excellent performance of the proposed methodology at the occurrence of gross outliers.

Training Efficient Network Architecture and Weights via Direct Sparsity Control

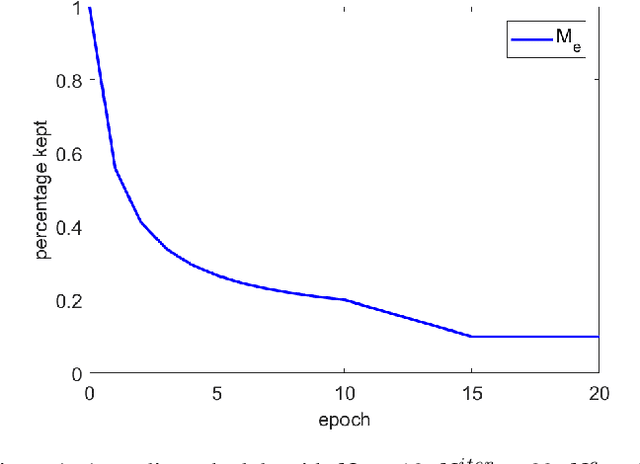
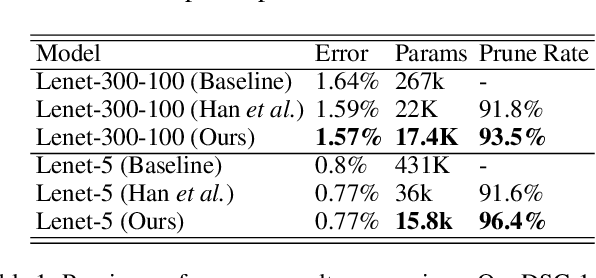
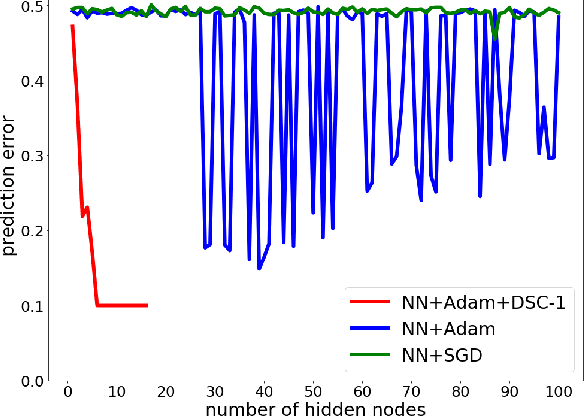
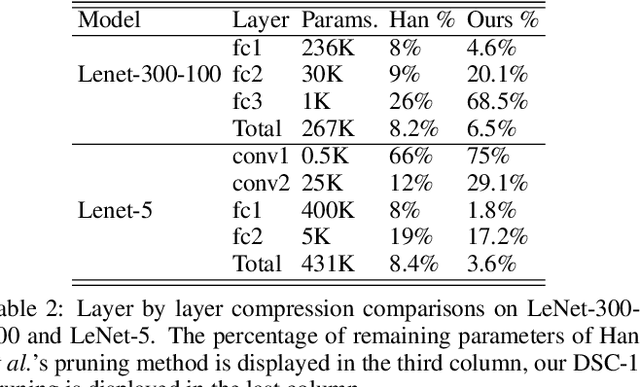
Artificial neural networks (ANNs) especially deep convolutional networks are very popular these days and have been proved to successfully offer quite reliable solutions to many vision problems. However, the use of deep neural networks is widely impeded by their intensive computational and memory cost. In this paper, we propose a novel efficient network pruning method that is suitable for both non-structured and structured channel-level pruning. Our proposed method tightens a sparsity constraint by gradually removing network parameters or filter channels based on a criterion and a schedule. The attractive fact that the network size keeps dropping throughout the iterations makes it suitable for the pruning of any untrained or pre-trained network. Because our method uses a L0 constraint instead of the L1 penalty, it does not introduce any bias in the training parameters or filter channels. Furthermore, the L0 constraint makes it easy to directly specify the desired sparsity level during the network pruning process. Finally, experimental validation on synthetic and real datasets both show that the proposed method obtains better or competitive performance compared to other states of art network pruning methods.

On Cross-validation for Sparse Reduced Rank Regression

In high-dimensional data analysis, regularization methods pursuing sparsity and/or low rank have received a lot of attention recently. To provide a proper amount of shrinkage, it is typical to use a grid search and a model comparison criterion to find the optimal regularization parameters. However, we show that fixing the parameters across all folds may result in an inconsistency issue, and it is more appropriate to cross-validate projection-selection patterns to obtain the best coefficient estimate. Our in-sample error studies in jointly sparse and rank-deficient models lead to a new class of information criteria with four scale-free forms to bypass the estimation of the noise level. By use of an identity, we propose a novel scale-free calibration to help cross-validation achieve the minimax optimal error rate non-asymptotically. Experiments support the efficacy of the proposed methods.

Iterative proportional scaling revisited: a modern optimization perspective

This paper revisits the classic iterative proportional scaling (IPS) from a modern optimization perspective. In contrast to the criticisms made in the literature, we show that based on a coordinate descent characterization, IPS can be slightly modified to deliver coefficient estimates, and from a majorization-minimization standpoint, IPS can be extended to handle log-affine models with features not necessarily binary-valued or nonnegative. Furthermore, some state-of-the-art optimization techniques such as block-wise computation, randomization and momentum-based acceleration can be employed to provide more scalable IPS algorithms, as well as some regularized variants of IPS for concurrent feature selection.

Group Regularized Estimation under Structural Hierarchy

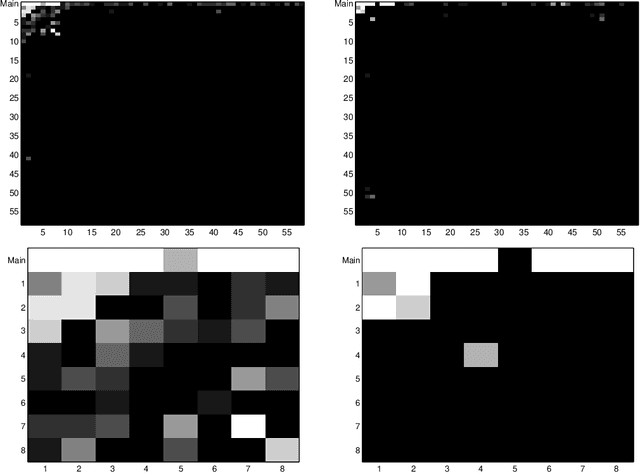
Variable selection for models including interactions between explanatory variables often needs to obey certain hierarchical constraints. The weak or strong structural hierarchy requires that the existence of an interaction term implies at least one or both associated main effects to be present in the model. Lately, this problem has attracted a lot of attention, but existing computational algorithms converge slow even with a moderate number of predictors. Moreover, in contrast to the rich literature on ordinary variable selection, there is a lack of statistical theory to show reasonably low error rates of hierarchical variable selection. This work investigates a new class of estimators that make use of multiple group penalties to capture structural parsimony. We give the minimax lower bounds for strong and weak hierarchical variable selection and show that the proposed estimators enjoy sharp rate oracle inequalities. A general-purpose algorithm is developed with guaranteed convergence and global optimality. Simulations and real data experiments demonstrate the efficiency and efficacy of the proposed approach.

Indirect Gaussian Graph Learning beyond Gaussianity

This paper studies how to capture dependency graph structures from real data which may not be multivariate Gaussian. Starting from marginal loss functions not necessarily derived from probability distributions, we use an additive over-parametrization with shrinkage to incorporate variable dependencies into the criterion. An iterative Gaussian graph learning algorithm is proposed with ease in implementation. Statistical analysis shows that with the error measured in terms of a proper Bregman divergence, the estimators have fast rate of convergence. Real-life examples in different settings are given to demonstrate the efficacy of the proposed methodology.