Supervised Multivariate Learning with Simultaneous Feature Auto-grouping and Dimension Reduction

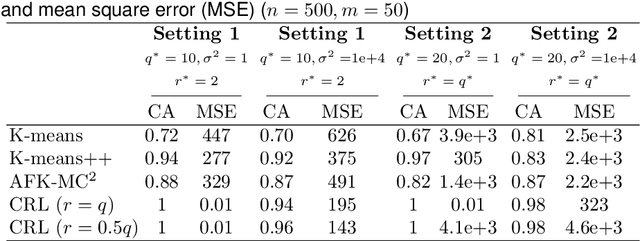
Modern high-dimensional methods often adopt the ``bet on sparsity'' principle, while in supervised multivariate learning statisticians may face ``dense'' problems with a large number of nonzero coefficients. This paper proposes a novel clustered reduced-rank learning (CRL) framework that imposes two joint matrix regularizations to automatically group the features in constructing predictive factors. CRL is more interpretable than low-rank modeling and relaxes the stringent sparsity assumption in variable selection. In this paper, new information-theoretical limits are presented to reveal the intrinsic cost of seeking for clusters, as well as the blessing from dimensionality in multivariate learning. Moreover, an efficient optimization algorithm is developed, which performs subspace learning and clustering with guaranteed convergence. The obtained fixed-point estimators, though not necessarily globally optimal, enjoy the desired statistical accuracy beyond the standard likelihood setup under some regularity conditions. Moreover, a new kind of information criterion, as well as its scale-free form, is proposed for cluster and rank selection, and has a rigorous theoretical support without assuming an infinite sample size. Extensive simulations and real-data experiments demonstrate the statistical accuracy and interpretability of the proposed method.

Gaining Outlier Resistance with Progressive Quantiles: Fast Algorithms and Theoretical Studies

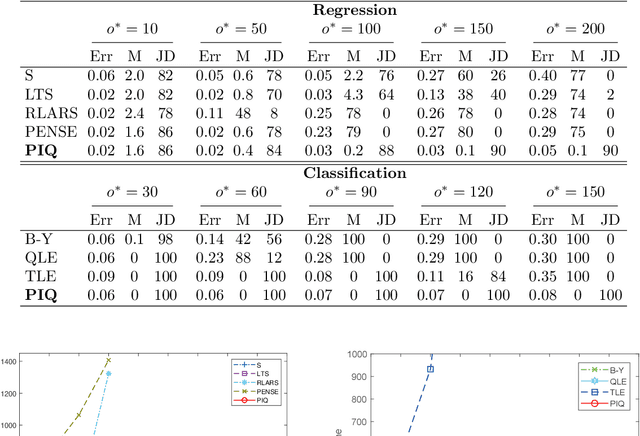
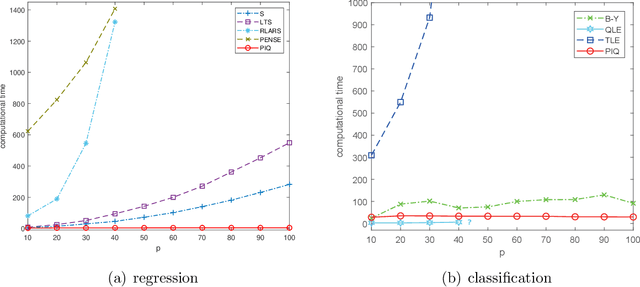
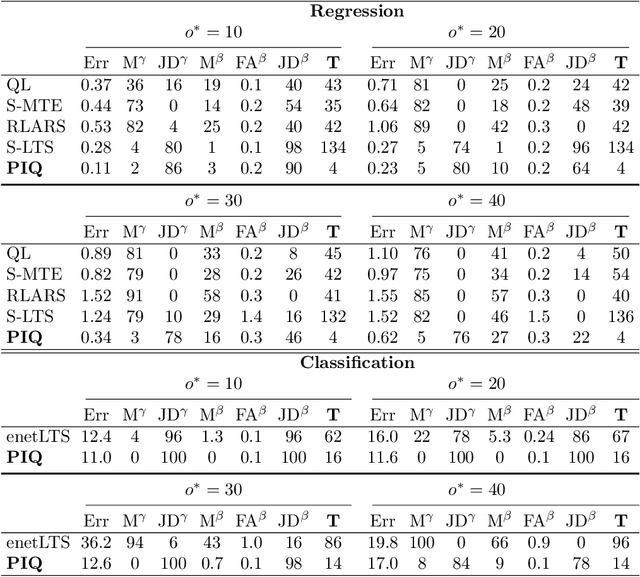
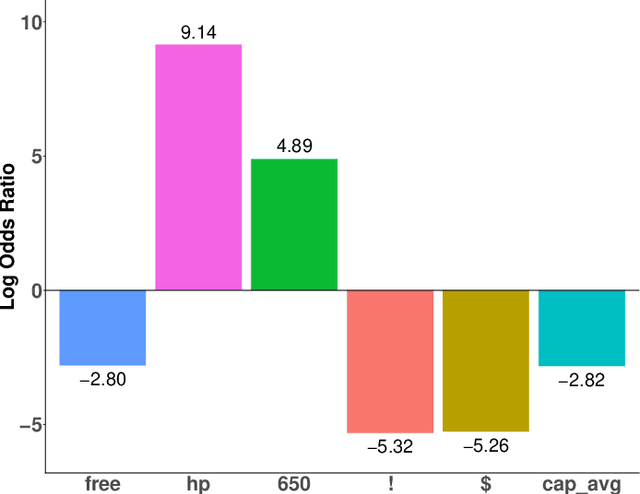
Outliers widely occur in big-data applications and may severely affect statistical estimation and inference. In this paper, a framework of outlier-resistant estimation is introduced to robustify an arbitrarily given loss function. It has a close connection to the method of trimming and includes explicit outlyingness parameters for all samples, which in turn facilitates computation, theory, and parameter tuning. To tackle the issues of nonconvexity and nonsmoothness, we develop scalable algorithms with implementation ease and guaranteed fast convergence. In particular, a new technique is proposed to alleviate the requirement on the starting point such that on regular datasets, the number of data resamplings can be substantially reduced. Based on combined statistical and computational treatments, we are able to perform nonasymptotic analysis beyond M-estimation. The obtained resistant estimators, though not necessarily globally or even locally optimal, enjoy minimax rate optimality in both low dimensions and high dimensions. Experiments in regression, classification, and neural networks show excellent performance of the proposed methodology at the occurrence of gross outliers.