Gaining Outlier Resistance with Progressive Quantiles: Fast Algorithms and Theoretical Studies
Paper and Code
Dec 15, 2021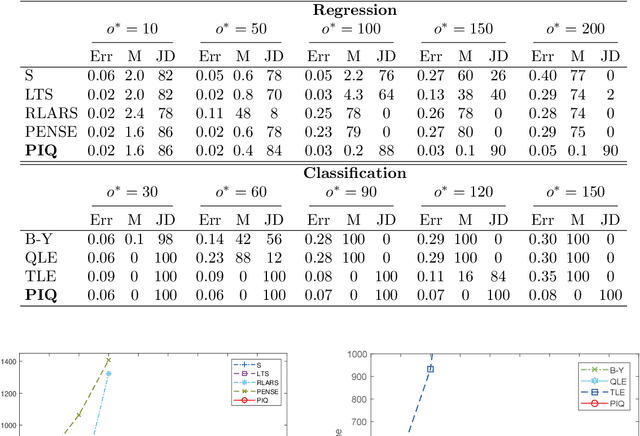
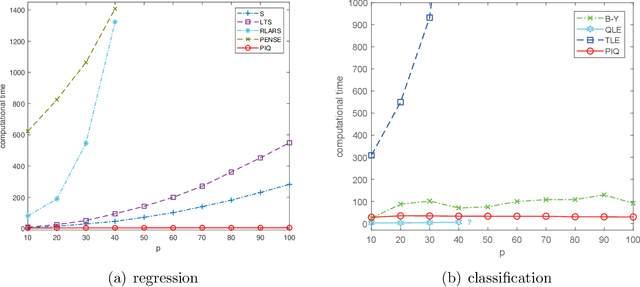
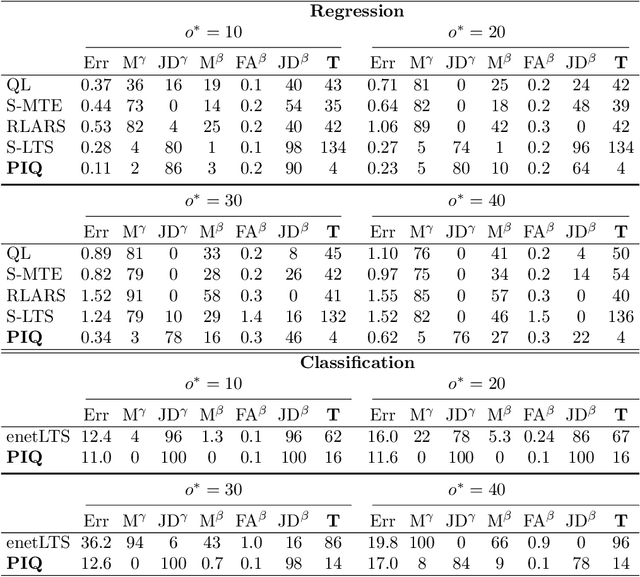
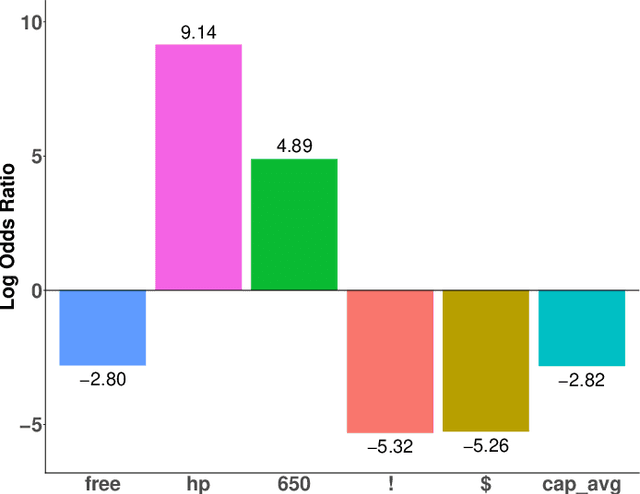
Outliers widely occur in big-data applications and may severely affect statistical estimation and inference. In this paper, a framework of outlier-resistant estimation is introduced to robustify an arbitrarily given loss function. It has a close connection to the method of trimming and includes explicit outlyingness parameters for all samples, which in turn facilitates computation, theory, and parameter tuning. To tackle the issues of nonconvexity and nonsmoothness, we develop scalable algorithms with implementation ease and guaranteed fast convergence. In particular, a new technique is proposed to alleviate the requirement on the starting point such that on regular datasets, the number of data resamplings can be substantially reduced. Based on combined statistical and computational treatments, we are able to perform nonasymptotic analysis beyond M-estimation. The obtained resistant estimators, though not necessarily globally or even locally optimal, enjoy minimax rate optimality in both low dimensions and high dimensions. Experiments in regression, classification, and neural networks show excellent performance of the proposed methodology at the occurrence of gross outliers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge