CoT-ICL Lab: A Petri Dish for Studying Chain-of-Thought Learning from In-Context Demonstrations

We introduce CoT-ICL Lab, a framework and methodology to generate synthetic tokenized datasets and systematically study chain-of-thought (CoT) in-context learning (ICL) in language models. CoT-ICL Lab allows fine grained control over the complexity of in-context examples by decoupling (1) the causal structure involved in chain token generation from (2) the underlying token processing functions. We train decoder-only transformers (up to 700M parameters) on these datasets and show that CoT accelerates the accuracy transition to higher values across model sizes. In particular, we find that model depth is crucial for leveraging CoT with limited in-context examples, while more examples help shallow models match deeper model performance. Additionally, limiting the diversity of token processing functions throughout training improves causal structure learning via ICL. We also interpret these transitions by analyzing transformer embeddings and attention maps. Overall, CoT-ICL Lab serves as a simple yet powerful testbed for theoretical and empirical insights into ICL and CoT in language models.

Efficient AI in Practice: Training and Deployment of Efficient LLMs for Industry Applications

Large language models (LLMs) have demonstrated remarkable performance across a wide range of industrial applications, from search and recommendations to generative tasks. Although scaling laws indicate that larger models generally yield better generalization and performance, their substantial computational requirements often render them impractical for many real-world scenarios at scale. In this paper, we present methods and insights for training small language models (SLMs) that deliver high performance and efficiency in deployment. We focus on two key techniques: (1) knowledge distillation and (2) model compression via quantization and pruning. These approaches enable SLMs to retain much of the quality of their larger counterparts while significantly reducing training, serving costs, and latency. We detail the impact of these techniques on a variety of use cases at a large professional social network platform and share deployment lessons - including hardware optimization strategies that enhance speed and throughput for both predictive and reasoning-based applications.

360Brew: A Decoder-only Foundation Model for Personalized Ranking and Recommendation

Ranking and recommendation systems are the foundation for numerous online experiences, ranging from search results to personalized content delivery. These systems have evolved into complex, multilayered architectures that leverage vast datasets and often incorporate thousands of predictive models. The maintenance and enhancement of these models is a labor intensive process that requires extensive feature engineering. This approach not only exacerbates technical debt but also hampers innovation in extending these systems to emerging problem domains. In this report, we present our research to address these challenges by utilizing a large foundation model with a textual interface for ranking and recommendation tasks. We illustrate several key advantages of our approach: (1) a single model can manage multiple predictive tasks involved in ranking and recommendation, (2) decoder models with textual interface due to their comprehension of reasoning capabilities, can generalize to new recommendation surfaces and out-of-domain problems, and (3) by employing natural language interfaces for task definitions and verbalizing member behaviors and their social connections, we eliminate the need for feature engineering and the maintenance of complex directed acyclic graphs of model dependencies. We introduce our research pre-production model, 360Brew V1.0, a 150B parameter, decoder-only model that has been trained and fine-tuned on LinkedIn's data and tasks. This model is capable of solving over 30 predictive tasks across various segments of the LinkedIn platform, achieving performance levels comparable to or exceeding those of current production systems based on offline metrics, without task-specific fine-tuning. Notably, each of these tasks is conventionally addressed by dedicated models that have been developed and maintained over multiple years by teams of a similar or larger size than our own.

Liger Kernel: Efficient Triton Kernels for LLM Training

Training Large Language Models (LLMs) efficiently at scale presents a formidable challenge, driven by their ever-increasing computational demands and the need for enhanced performance. In this work, we introduce Liger-Kernel, an open-sourced set of Triton kernels developed specifically for LLM training. With kernel optimization techniques like kernel operation fusing and input chunking, our kernels achieve on average a 20% increase in training throughput and a 60% reduction in GPU memory usage for popular LLMs compared to HuggingFace implementations. In addition, Liger-Kernel is designed with modularity, accessibility, and adaptability in mind, catering to both casual and expert users. Comprehensive benchmarks and integration tests are built in to ensure compatibility, performance, correctness, and convergence across diverse computing environments and model architectures. The source code is available under a permissive license at: github.com/linkedin/Liger-Kernel.

Crafting Heavy-Tails in Weight Matrix Spectrum without Gradient Noise

Modern training strategies of deep neural networks (NNs) tend to induce a heavy-tailed (HT) spectra of layer weights. Extensive efforts to study this phenomenon have found that NNs with HT weight spectra tend to generalize well. A prevailing notion for the occurrence of such HT spectra attributes gradient noise during training as a key contributing factor. Our work shows that gradient noise is unnecessary for generating HT weight spectra: two-layer NNs trained with full-batch Gradient Descent/Adam can exhibit HT spectra in their weights after finite training steps. To this end, we first identify the scale of the learning rate at which one step of full-batch Adam can lead to feature learning in the shallow NN, particularly when learning a single index teacher model. Next, we show that multiple optimizer steps with such (sufficiently) large learning rates can transition the bulk of the weight's spectra into an HT distribution. To understand this behavior, we present a novel perspective based on the singular vectors of the weight matrices and optimizer updates. We show that the HT weight spectrum originates from the `spike', which is generated from feature learning and interacts with the main bulk to generate an HT spectrum. Finally, we analyze the correlations between the HT weight spectra and generalization after multiple optimizer updates with varying learning rates.

Kernel vs. Kernel: Exploring How the Data Structure Affects Neural Collapse

Recently, a vast amount of literature has focused on the "Neural Collapse" (NC) phenomenon, which emerges when training neural network (NN) classifiers beyond the zero training error point. The core component of NC is the decrease in the within class variability of the network's deepest features, dubbed as NC1. The theoretical works that study NC are typically based on simplified unconstrained features models (UFMs) that mask any effect of the data on the extent of collapse. In this paper, we provide a kernel-based analysis that does not suffer from this limitation. First, given a kernel function, we establish expressions for the traces of the within- and between-class covariance matrices of the samples' features (and consequently an NC1 metric). Then, we turn to focus on kernels associated with shallow NNs. First, we consider the NN Gaussian Process kernel (NNGP), associated with the network at initialization, and the complement Neural Tangent Kernel (NTK), associated with its training in the "lazy regime". Interestingly, we show that the NTK does not represent more collapsed features than the NNGP for prototypical data models. As NC emerges from training, we then consider an alternative to NTK: the recently proposed adaptive kernel, which generalizes NNGP to model the feature mapping learned from the training data. Contrasting our NC1 analysis for these two kernels enables gaining insights into the effect of data distribution on the extent of collapse, which are empirically aligned with the behavior observed with practical training of NNs.

A Neural Collapse Perspective on Feature Evolution in Graph Neural Networks

Graph neural networks (GNNs) have become increasingly popular for classification tasks on graph-structured data. Yet, the interplay between graph topology and feature evolution in GNNs is not well understood. In this paper, we focus on node-wise classification, illustrated with community detection on stochastic block model graphs, and explore the feature evolution through the lens of the "Neural Collapse" (NC) phenomenon. When training instance-wise deep classifiers (e.g. for image classification) beyond the zero training error point, NC demonstrates a reduction in the deepest features' within-class variability and an increased alignment of their class means to certain symmetric structures. We start with an empirical study that shows that a decrease in within-class variability is also prevalent in the node-wise classification setting, however, not to the extent observed in the instance-wise case. Then, we theoretically study this distinction. Specifically, we show that even an "optimistic" mathematical model requires that the graphs obey a strict structural condition in order to possess a minimizer with exact collapse. Interestingly, this condition is viable also for heterophilic graphs and relates to recent empirical studies on settings with improved GNNs' generalization. Furthermore, by studying the gradient dynamics of the theoretical model, we provide reasoning for the partial collapse observed empirically. Finally, we present a study on the evolution of within- and between-class feature variability across layers of a well-trained GNN and contrast the behavior with spectral methods.

Randomized Schur Complement Views for Graph Contrastive Learning

We introduce a randomized topological augmentor based on Schur complements for Graph Contrastive Learning (GCL). Given a graph laplacian matrix, the technique generates unbiased approximations of its Schur complements and treats the corresponding graphs as augmented views. We discuss the benefits of our approach, provide theoretical justifications and present connections with graph diffusion. Unlike previous efforts, we study the empirical effectiveness of the augmentor in a controlled fashion by varying the design choices for subsequent GCL phases, such as encoding and contrasting. Extensive experiments on node and graph classification benchmarks demonstrate that our technique consistently outperforms pre-defined and adaptive augmentation approaches to achieve state-of-the-art results.

Neural Collapse: A Review on Modelling Principles and Generalization

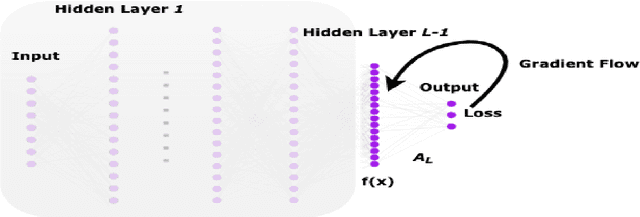
With a recent observation of the "Neural Collapse (NC)" phenomena by Papyan et al., various efforts have been made to model it and analyse the implications. Neural collapse describes that in deep classifier networks, the class features of the final hidden layer associated with training data tend to collapse to the respective class feature means. Thus, simplifying the behaviour of the last layer classifier to that of a nearest-class center decision rule. In this work, we analyse the principles which aid in modelling such a phenomena from the ground up and show how they can build a common understanding of the recently proposed models that try to explain NC. We hope that our analysis presents a multifaceted perspective on modelling NC and aids in forming connections with the generalization capabilities of neural networks. Finally, we conclude by discussing the avenues for further research and propose potential research problems.