Does the Data Processing Inequality Reflect Practice? On the Utility of Low-Level Tasks

The data processing inequality is an information-theoretic principle stating that the information content of a signal cannot be increased by processing the observations. In particular, it suggests that there is no benefit in enhancing the signal or encoding it before addressing a classification problem. This assertion can be proven to be true for the case of the optimal Bayes classifier. However, in practice, it is common to perform "low-level" tasks before "high-level" downstream tasks despite the overwhelming capabilities of modern deep neural networks. In this paper, we aim to understand when and why low-level processing can be beneficial for classification. We present a comprehensive theoretical study of a binary classification setup, where we consider a classifier that is tightly connected to the optimal Bayes classifier and converges to it as the number of training samples increases. We prove that for any finite number of training samples, there exists a pre-classification processing that improves the classification accuracy. We also explore the effect of class separation, training set size, and class balance on the relative gain from this procedure. We support our theory with an empirical investigation of the theoretical setup. Finally, we conduct an empirical study where we investigate the effect of denoising and encoding on the performance of practical deep classifiers on benchmark datasets. Specifically, we vary the size and class distribution of the training set, and the noise level, and demonstrate trends that are consistent with our theoretical results.

Efficient Conformal Prediction for Regression Models under Label Noise

In high-stakes scenarios, such as medical imaging applications, it is critical to equip the predictions of a regression model with reliable confidence intervals. Recently, Conformal Prediction (CP) has emerged as a powerful statistical framework that, based on a labeled calibration set, generates intervals that include the true labels with a pre-specified probability. In this paper, we address the problem of applying CP for regression models when the calibration set contains noisy labels. We begin by establishing a mathematically grounded procedure for estimating the noise-free CP threshold. Then, we turn it into a practical algorithm that overcomes the challenges arising from the continuous nature of the regression problem. We evaluate the proposed method on two medical imaging regression datasets with Gaussian label noise. Our method significantly outperforms the existing alternative, achieving performance close to the clean-label setting.

(SP)$^2$-Net: A Neural Spatial Spectrum Method for DOA Estimation

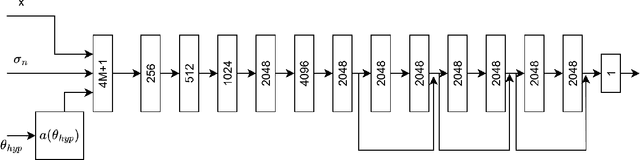
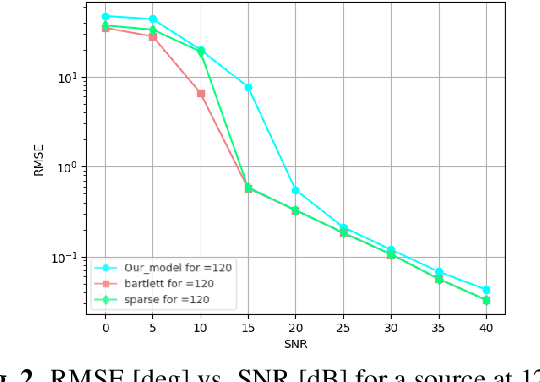
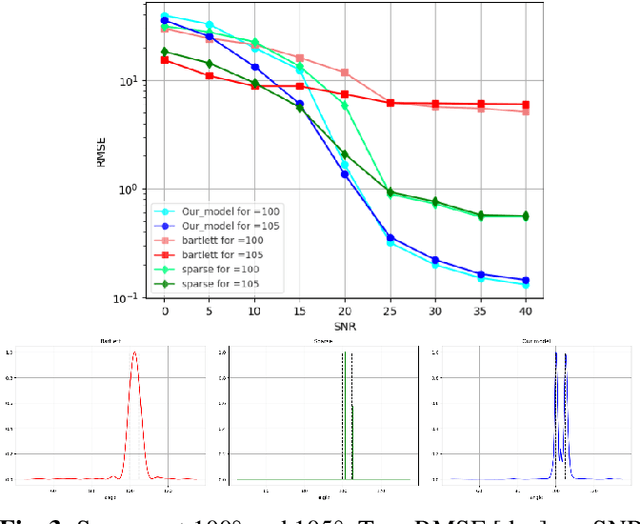
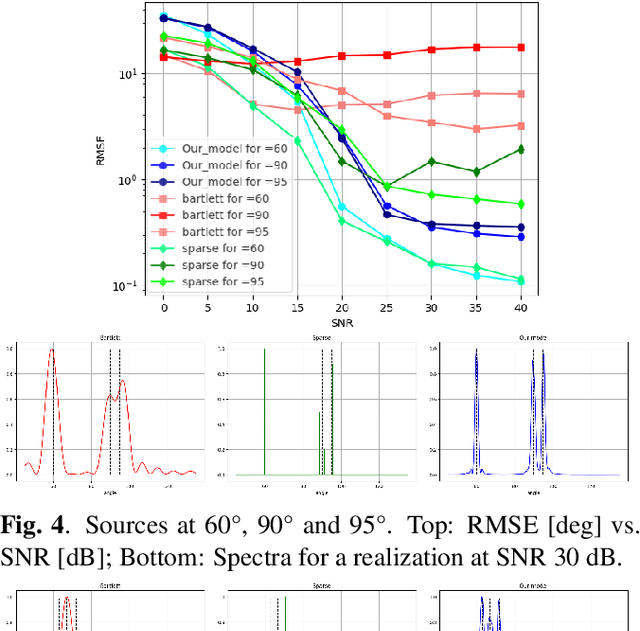
We consider the problem of estimating the directions of arrival (DOAs) of multiple sources from a single snapshot of an antenna array, a task with many practical applications. In such settings, the classical Bartlett beamformer is commonly used, as maximum likelihood estimation becomes impractical when the number of sources is unknown or large, and spectral methods based on the sample covariance are not applicable due to the lack of multiple snapshots. However, the accuracy and resolution of the Bartlett beamformer are fundamentally limited by the array aperture. In this paper, we propose a deep learning technique, comprising a novel architecture and training strategy, for generating a high-resolution spatial spectrum from a single snapshot. Specifically, we train a deep neural network that takes the measurements and a hypothesis angle as input and learns to output a score consistent with the capabilities of a much wider array. At inference time, a heatmap can be produced by scanning an arbitrary set of angles. We demonstrate the advantages of our trained model, named (SP)$^2$-Net, over the Bartlett beamformer and sparsity-based DOA estimation methods.

SUMO: Subspace-Aware Moment-Orthogonalization for Accelerating Memory-Efficient LLM Training

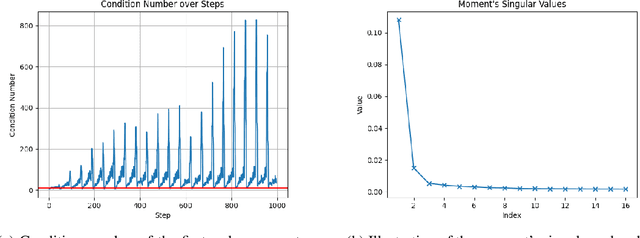
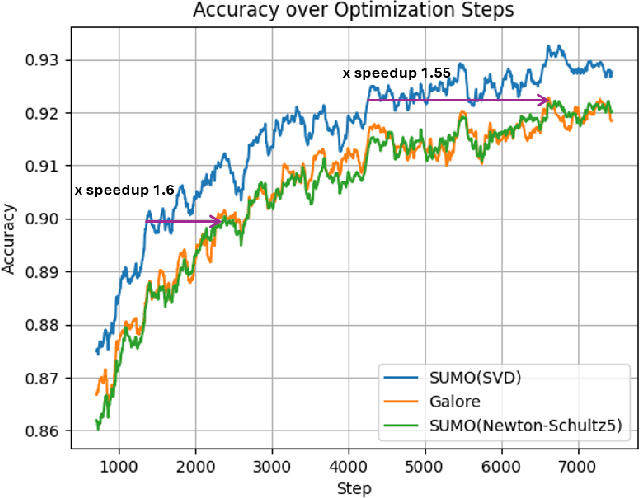
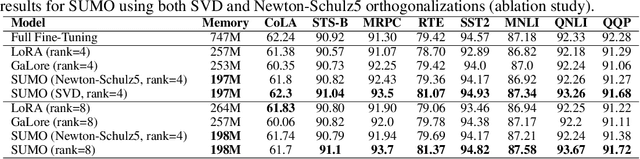
Low-rank gradient-based optimization methods have significantly improved memory efficiency during the training of large language models (LLMs), enabling operations within constrained hardware without sacrificing performance. However, these methods primarily emphasize memory savings, often overlooking potential acceleration in convergence due to their reliance on standard isotropic steepest descent techniques, which can perform suboptimally in the highly anisotropic landscapes typical of deep networks, particularly LLMs. In this paper, we propose SUMO (Subspace-Aware Moment-Orthogonalization), an optimizer that employs exact singular value decomposition (SVD) for moment orthogonalization within a dynamically adapted low-dimensional subspace, enabling norm-inducing steepest descent optimization steps. By explicitly aligning optimization steps with the spectral characteristics of the loss landscape, SUMO effectively mitigates approximation errors associated with commonly used methods like Newton-Schulz orthogonalization approximation. We theoretically establish an upper bound on these approximation errors, proving their dependence on the condition numbers of moments, conditions we analytically demonstrate are encountered during LLM training. Furthermore, we both theoretically and empirically illustrate that exact orthogonalization via SVD substantially improves convergence rates while reducing overall complexity. Empirical evaluations confirm that SUMO accelerates convergence, enhances stability, improves performance, and reduces memory requirements by up to 20% compared to state-of-the-art methods.

LORENZA: Enhancing Generalization in Low-Rank Gradient LLM Training via Efficient Zeroth-Order Adaptive SAM

We study robust parameter-efficient fine-tuning (PEFT) techniques designed to improve accuracy and generalization while operating within strict computational and memory hardware constraints, specifically focusing on large-language models (LLMs). Existing PEFT methods often lack robustness and fail to generalize effectively across diverse tasks, leading to suboptimal performance in real-world scenarios. To address this, we present a new highly computationally efficient framework called AdaZo-SAM, combining Adam and Sharpness-Aware Minimization (SAM) while requiring only a single-gradient computation in every iteration. This is achieved using a stochastic zeroth-order estimation to find SAM's ascent perturbation. We provide a convergence guarantee for AdaZo-SAM and show that it improves the generalization ability of state-of-the-art PEFT methods. Additionally, we design a low-rank gradient optimization method named LORENZA, which is a memory-efficient version of AdaZo-SAM. LORENZA utilizes a randomized SVD scheme to efficiently compute the subspace projection matrix and apply optimization steps onto the selected subspace. This technique enables full-parameter fine-tuning with adaptive low-rank gradient updates, achieving the same reduced memory consumption as gradient-low-rank-projection methods. We provide a convergence analysis of LORENZA and demonstrate its merits for pre-training and fine-tuning LLMs.

Zero-Shot Image Restoration Using Few-Step Guidance of Consistency Models (and Beyond)

In recent years, it has become popular to tackle image restoration tasks with a single pretrained diffusion model (DM) and data-fidelity guidance, instead of training a dedicated deep neural network per task. However, such "zero-shot" restoration schemes currently require many Neural Function Evaluations (NFEs) for performing well, which may be attributed to the many NFEs needed in the original generative functionality of the DMs. Recently, faster variants of DMs have been explored for image generation. These include Consistency Models (CMs), which can generate samples via a couple of NFEs. However, existing works that use guided CMs for restoration still require tens of NFEs or fine-tuning of the model per task that leads to performance drop if the assumptions during the fine-tuning are not accurate. In this paper, we propose a zero-shot restoration scheme that uses CMs and operates well with as little as 4 NFEs. It is based on a wise combination of several ingredients: better initialization, back-projection guidance, and above all a novel noise injection mechanism. We demonstrate the advantages of our approach for image super-resolution, deblurring and inpainting. Interestingly, we show that the usefulness of our noise injection technique goes beyond CMs: it can also mitigate the performance degradation of existing guided DM methods when reducing their NFE count.

Multiple Descents in Unsupervised Learning: The Role of Noise, Domain Shift and Anomalies

The phenomenon of double descent has recently gained attention in supervised learning. It challenges the conventional wisdom of the bias-variance trade-off by showcasing a surprising behavior. As the complexity of the model increases, the test error initially decreases until reaching a certain point where the model starts to overfit the train set, causing the test error to rise. However, deviating from classical theory, the error exhibits another decline when exceeding a certain degree of over-parameterization. We study the presence of double descent in unsupervised learning, an area that has received little attention and is not yet fully understood. We conduct extensive experiments using under-complete auto-encoders (AEs) for various applications, such as dealing with noisy data, domain shifts, and anomalies. We use synthetic and real data and identify model-wise, epoch-wise, and sample-wise double descent for all the aforementioned applications. Finally, we assessed the usability of the AEs for detecting anomalies and mitigating the domain shift between datasets. Our findings indicate that over-parameterized models can improve performance not only in terms of reconstruction, but also in enhancing capabilities for the downstream task.

Kernel vs. Kernel: Exploring How the Data Structure Affects Neural Collapse

Recently, a vast amount of literature has focused on the "Neural Collapse" (NC) phenomenon, which emerges when training neural network (NN) classifiers beyond the zero training error point. The core component of NC is the decrease in the within class variability of the network's deepest features, dubbed as NC1. The theoretical works that study NC are typically based on simplified unconstrained features models (UFMs) that mask any effect of the data on the extent of collapse. In this paper, we provide a kernel-based analysis that does not suffer from this limitation. First, given a kernel function, we establish expressions for the traces of the within- and between-class covariance matrices of the samples' features (and consequently an NC1 metric). Then, we turn to focus on kernels associated with shallow NNs. First, we consider the NN Gaussian Process kernel (NNGP), associated with the network at initialization, and the complement Neural Tangent Kernel (NTK), associated with its training in the "lazy regime". Interestingly, we show that the NTK does not represent more collapsed features than the NNGP for prototypical data models. As NC emerges from training, we then consider an alternative to NTK: the recently proposed adaptive kernel, which generalizes NNGP to model the feature mapping learned from the training data. Contrasting our NC1 analysis for these two kernels enables gaining insights into the effect of data distribution on the extent of collapse, which are empirically aligned with the behavior observed with practical training of NNs.

On Calibration and Conformal Prediction of Deep Classifiers

In many classification applications, the prediction of a deep neural network (DNN) based classifier needs to be accompanied with some confidence indication. Two popular post-processing approaches for that aim are: 1) calibration: modifying the classifier's softmax values such that their maximum (associated with the prediction) better estimates the correctness probability; and 2) conformal prediction (CP): devising a score (based on the softmax values) from which a set of predictions with theoretically guaranteed marginal coverage of the correct class is produced. While in practice both types of indications can be desired, so far the interplay between them has not been investigated. Toward filling this gap, in this paper we study the effect of temperature scaling, arguably the most common calibration technique, on prominent CP methods. We start with an extensive empirical study that among other insights shows that, surprisingly, calibration has a detrimental effect on popular adaptive CP methods: it frequently leads to larger prediction sets. Then, we turn to theoretically analyze this behavior. We reveal several mathematical properties of the procedure, according to which we provide a reasoning for the phenomenon. Our study suggests that it may be worthwhile to utilize adaptive CP methods, chosen for their enhanced conditional coverage, based on softmax values prior to (or after canceling) temperature scaling calibration.

Image Restoration by Denoising Diffusion Models with Iteratively Preconditioned Guidance

Training deep neural networks has become a common approach for addressing image restoration problems. An alternative for training a "task-specific" network for each observation model is to use pretrained deep denoisers for imposing only the signal's prior within iterative algorithms, without additional training. Recently, a sampling-based variant of this approach has become popular with the rise of diffusion/score-based generative models. Using denoisers for general purpose restoration requires guiding the iterations to ensure agreement of the signal with the observations. In low-noise settings, guidance that is based on back-projection (BP) has been shown to be a promising strategy (used recently also under the names "pseudoinverse" or "range/null-space" guidance). However, the presence of noise in the observations hinders the gains from this approach. In this paper, we propose a novel guidance technique, based on preconditioning that allows traversing from BP-based guidance to least squares based guidance along the restoration scheme. The proposed approach is robust to noise while still having much simpler implementation than alternative methods (e.g., it does not require SVD or a large number of iterations). We use it within both an optimization scheme and a sampling-based scheme, and demonstrate its advantages over existing methods for image deblurring and super-resolution.