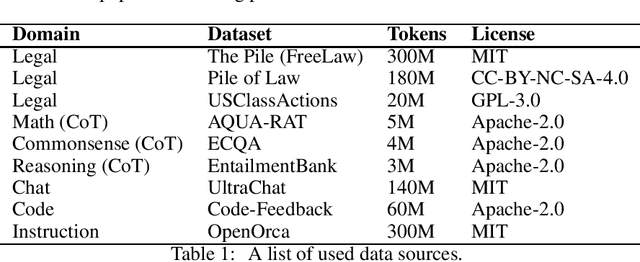
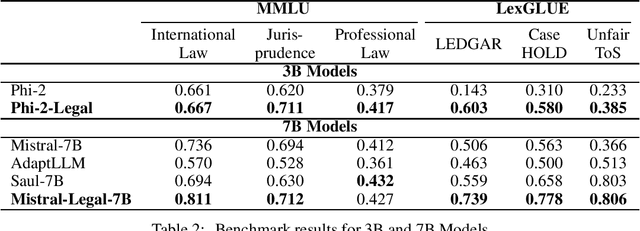
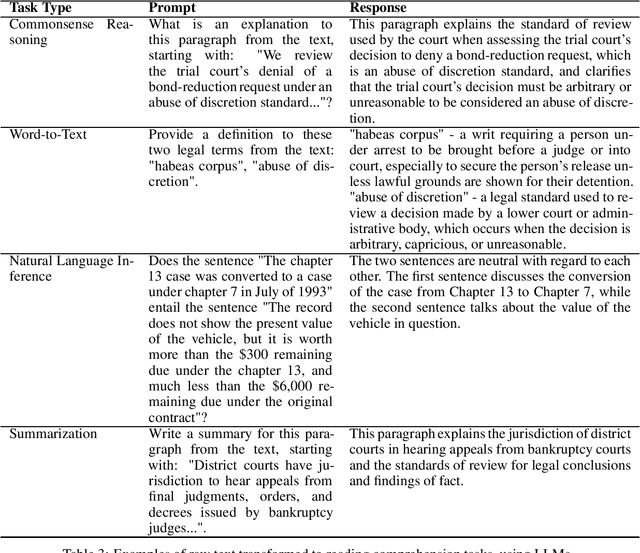
TransformLLM: Adapting Large Language Models via LLM-Transformed Reading Comprehension Text

Large Language Models (LLMs) have shown promise in highly-specialized domains, however challenges are still present in aspects of accuracy and costs. These limitations restrict the usage of existing models in domain-specific tasks. While fine-tuning pre-trained models have shown promising results, this process can be computationally expensive and require massive datasets of the specialized application in hand. In this work, we bridge that gap. We have developed Phi-2-Legal and Mistral-Legal-7B, which are language models specifically designed for legal applications. These models are based on Phi-2 and Mistral-7B-v0.1, and have gone through continued pre-training with over 500 million tokens of legal texts. Our innovative approach significantly improves capabilities in legal tasks by using Large Language Models (LLMs) to convert raw training data into reading comprehension text. Our legal LLMs have demonstrated superior performance in legal benchmarks, even outperforming models trained on much larger datasets with more resources. This work emphasizes the effectiveness of continued pre-training on domain-specific texts, while using affordable LLMs for data conversion, which gives these models domain expertise while retaining general language understanding capabilities. While this work uses the legal domain as a test case, our method can be scaled and applied to any pre-training dataset, resulting in significant improvements across different tasks. These findings underscore the potential of domain-adaptive pre-training and reading comprehension for the development of highly effective domain-specific language models.

Learning k-Level Sparse Neural Networks Using a New Generalized Group Sparse Envelope Regularization

We propose an efficient method to learn both unstructured and structured sparse neural networks during training, using a novel generalization of the sparse envelope function (SEF) used as a regularizer, termed {\itshape{group sparse envelope function}} (GSEF). The GSEF acts as a neuron group selector, which we leverage to induce structured pruning. Our method receives a hardware-friendly structured sparsity of a deep neural network (DNN) to efficiently accelerate the DNN's evaluation. This method is flexible in the sense that it allows any hardware to dictate the definition of a group, such as a filter, channel, filter shape, layer depth, a single parameter (unstructured), etc. By the nature of the GSEF, the proposed method is the first to make possible a pre-define sparsity level that is being achieved at the training convergence, while maintaining negligible network accuracy degradation. We propose an efficient method to calculate the exact value of the GSEF along with its proximal operator, in a worst-case complexity of $O(n)$, where $n$ is the total number of groups variables. In addition, we propose a proximal-gradient-based optimization method to train the model, that is, the non-convex minimization of the sum of the neural network loss and the GSEF. Finally, we conduct an experiment and illustrate the efficiency of our proposed technique in terms of the completion ratio, accuracy, and inference latency.