Wasim Huleihel
Expectation-maximization for multi-reference alignment: Two pitfalls and one remedy
May 27, 2025Abstract:We study the multi-reference alignment model, which involves recovering a signal from noisy observations that have been randomly transformed by an unknown group action, a fundamental challenge in statistical signal processing, computational imaging, and structural biology. While much of the theoretical literature has focused on the asymptotic sample complexity of this model, the practical performance of reconstruction algorithms, particularly of the omnipresent expectation maximization (EM) algorithm, remains poorly understood. In this work, we present a detailed investigation of EM in the challenging low signal-to-noise ratio (SNR) regime. We identify and characterize two failure modes that emerge in this setting. The first, called Einstein from Noise, reveals a strong sensitivity to initialization, with reconstructions resembling the input template regardless of the true underlying signal. The second phenomenon, referred to as the Ghost of Newton, involves EM initially converging towards the correct solution but later diverging, leading to a loss of reconstruction fidelity. We provide theoretical insights and support our findings through numerical experiments. Finally, we introduce a simple, yet effective modification to EM based on mini-batching, which mitigates the above artifacts. Supported by both theory and experiments, this mini-batching approach processes small data subsets per iteration, reducing initialization bias and computational cost, while maintaining accuracy comparable to full-batch EM.
Detecting Arbitrary Planted Subgraphs in Random Graphs
Mar 24, 2025Abstract:The problems of detecting and recovering planted structures/subgraphs in Erd\H{o}s-R\'{e}nyi random graphs, have received significant attention over the past three decades, leading to many exciting results and mathematical techniques. However, prior work has largely focused on specific ad hoc planted structures and inferential settings, while a general theory has remained elusive. In this paper, we bridge this gap by investigating the detection of an \emph{arbitrary} planted subgraph $\Gamma = \Gamma_n$ in an Erd\H{o}s-R\'{e}nyi random graph $\mathcal{G}(n, q_n)$, where the edge probability within $\Gamma$ is $p_n$. We examine both the statistical and computational aspects of this problem and establish the following results. In the dense regime, where the edge probabilities $p_n$ and $q_n$ are fixed, we tightly characterize the information-theoretic and computational thresholds for detecting $\Gamma$, and provide conditions under which a computational-statistical gap arises. Most notably, these thresholds depend on $\Gamma$ only through its number of edges, maximum degree, and maximum subgraph density. Our lower and upper bounds are general and apply to any value of $p_n$ and $q_n$ as functions of $n$. Accordingly, we also analyze the sparse regime where $q_n = \Theta(n^{-\alpha})$ and $p_n-q_n =\Theta(q_n)$, with $\alpha\in[0,2]$, as well as the critical regime where $p_n=1-o(1)$ and $q_n = \Theta(n^{-\alpha})$, both of which have been widely studied, for specific choices of $\Gamma$. For these regimes, we show that our bounds are tight for all planted subgraphs investigated in the literature thus far\textemdash{}and many more. Finally, we identify conditions under which detection undergoes sharp phase transition, where the boundaries at which algorithms succeed or fail shift abruptly as a function of $q_n$.
AdaRankGrad: Adaptive Gradient-Rank and Moments for Memory-Efficient LLMs Training and Fine-Tuning
Oct 23, 2024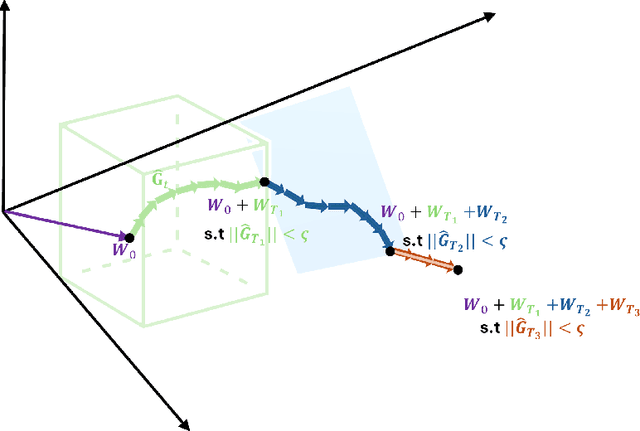
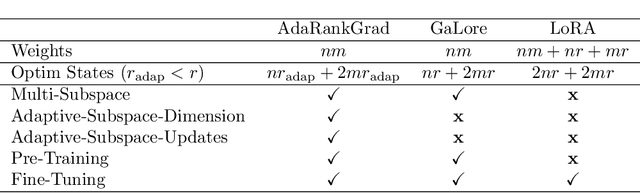
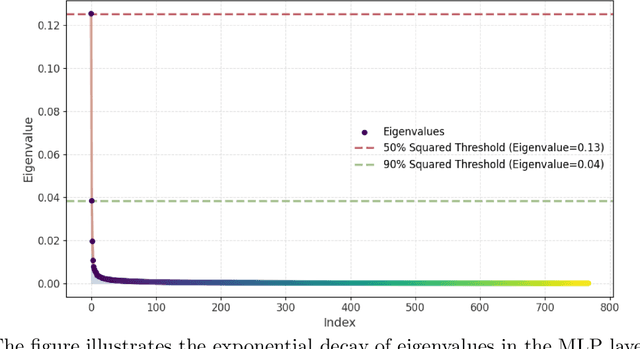

Abstract:Training and fine-tuning large language models (LLMs) come with challenges related to memory and computational requirements due to the increasing size of the model weights and the optimizer states. Various techniques have been developed to tackle these challenges, such as low-rank adaptation (LoRA), which involves introducing a parallel trainable low-rank matrix to the fixed pre-trained weights at each layer. However, these methods often fall short compared to the full-rank weight training approach, as they restrict the parameter search to a low-rank subspace. This limitation can disrupt training dynamics and require a full-rank warm start to mitigate the impact. In this paper, we introduce a new method inspired by a phenomenon we formally prove: as training progresses, the rank of the estimated layer gradients gradually decreases, and asymptotically approaches rank one. Leveraging this, our approach involves adaptively reducing the rank of the gradients during Adam optimization steps, using an efficient online-updating low-rank projections rule. We further present a randomized SVD scheme for efficiently finding the projection matrix. Our technique enables full-parameter fine-tuning with adaptive low-rank gradient updates, significantly reducing overall memory requirements during training compared to state-of-the-art methods while improving model performance in both pretraining and fine-tuning. Finally, we provide a convergence analysis of our method and demonstrate its merits for training and fine-tuning language and biological foundation models.
Sequential Classification of Misinformation
Sep 07, 2024
Abstract:In recent years there have been a growing interest in online auditing of information flow over social networks with the goal of monitoring undesirable effects, such as, misinformation and fake news. Most previous work on the subject, focus on the binary classification problem of classifying information as fake or genuine. Nonetheless, in many practical scenarios, the multi-class/label setting is of particular importance. For example, it could be the case that a social media platform may want to distinguish between ``true", ``partly-true", and ``false" information. Accordingly, in this paper, we consider the problem of online multiclass classification of information flow. To that end, driven by empirical studies on information flow over real-world social media networks, we propose a probabilistic information flow model over graphs. Then, the learning task is to detect the label of the information flow, with the goal of minimizing a combination of the classification error and the detection time. For this problem, we propose two detection algorithms; the first is based on the well-known multiple sequential probability ratio test, while the second is a novel graph neural network based sequential decision algorithm. For both algorithms, we prove several strong statistical guarantees. We also construct a data driven algorithm for learning the proposed probabilistic model. Finally, we test our algorithms over two real-world datasets, and show that they outperform other state-of-the-art misinformation detection algorithms, in terms of detection time and classification error.
Confirmation Bias in Gaussian Mixture Models
Aug 19, 2024Abstract:Confirmation bias, the tendency to interpret information in a way that aligns with one's preconceptions, can profoundly impact scientific research, leading to conclusions that reflect the researcher's hypotheses even when the observational data do not support them. This issue is especially critical in scientific fields involving highly noisy observations, such as cryo-electron microscopy. This study investigates confirmation bias in Gaussian mixture models. We consider the following experiment: A team of scientists assumes they are analyzing data drawn from a Gaussian mixture model with known signals (hypotheses) as centroids. However, in reality, the observations consist entirely of noise without any informative structure. The researchers use a single iteration of the K-means or expectation-maximization algorithms, two popular algorithms to estimate the centroids. Despite the observations being pure noise, we show that these algorithms yield biased estimates that resemble the initial hypotheses, contradicting the unbiased expectation that averaging these noise observations would converge to zero. Namely, the algorithms generate estimates that mirror the postulated model, although the hypotheses (the presumed centroids of the Gaussian mixture) are not evident in the observations. Specifically, among other results, we prove a positive correlation between the estimates produced by the algorithms and the corresponding hypotheses. We also derive explicit closed-form expressions of the estimates for a finite and infinite number of hypotheses. This study underscores the risks of confirmation bias in low signal-to-noise environments, provides insights into potential pitfalls in scientific methodologies, and highlights the importance of prudent data interpretation.
Einstein from Noise: Statistical Analysis
Jul 07, 2024Abstract:``Einstein from noise" (EfN) is a prominent example of the model bias phenomenon: systematic errors in the statistical model that lead to erroneous but consistent estimates. In the EfN experiment, one falsely believes that a set of observations contains noisy, shifted copies of a template signal (e.g., an Einstein image), whereas in reality, it contains only pure noise observations. To estimate the signal, the observations are first aligned with the template using cross-correlation, and then averaged. Although the observations contain nothing but noise, it was recognized early on that this process produces a signal that resembles the template signal! This pitfall was at the heart of a central scientific controversy about validation techniques in structural biology. This paper provides a comprehensive statistical analysis of the EfN phenomenon above. We show that the Fourier phases of the EfN estimator (namely, the average of the aligned noise observations) converge to the Fourier phases of the template signal, explaining the observed structural similarity. Additionally, we prove that the convergence rate is inversely proportional to the number of noise observations and, in the high-dimensional regime, to the Fourier magnitudes of the template signal. Moreover, in the high-dimensional regime, the Fourier magnitudes converge to a scaled version of the template signal's Fourier magnitudes. This work not only deepens the theoretical understanding of the EfN phenomenon but also highlights potential pitfalls in template matching techniques and emphasizes the need for careful interpretation of noisy observations across disciplines in engineering, statistics, physics, and biology.
Detection of Correlated Random Vectors
Jan 28, 2024
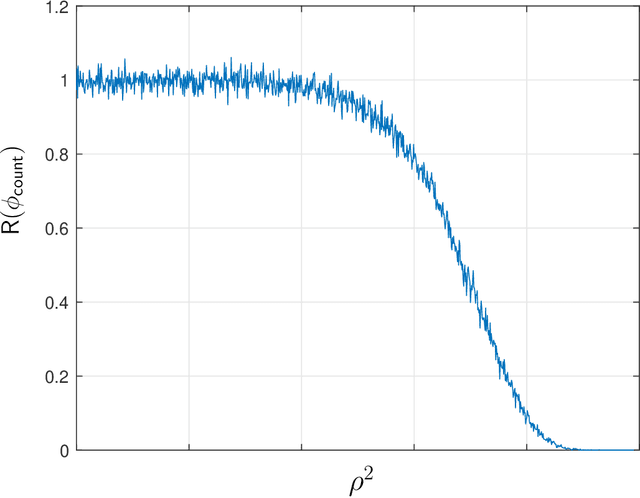

Abstract:In this paper, we investigate the problem of deciding whether two standard normal random vectors $\mathsf{X}\in\mathbb{R}^{n}$ and $\mathsf{Y}\in\mathbb{R}^{n}$ are correlated or not. This is formulated as a hypothesis testing problem, where under the null hypothesis, these vectors are statistically independent, while under the alternative, $\mathsf{X}$ and a randomly and uniformly permuted version of $\mathsf{Y}$, are correlated with correlation $\rho$. We analyze the thresholds at which optimal testing is information-theoretically impossible and possible, as a function of $n$ and $\rho$. To derive our information-theoretic lower bounds, we develop a novel technique for evaluating the second moment of the likelihood ratio using an orthogonal polynomials expansion, which among other things, reveals a surprising connection to integer partition functions. We also study a multi-dimensional generalization of the above setting, where rather than two vectors we observe two databases/matrices, and furthermore allow for partial correlations between these two.
Testing Dependency of Unlabeled Databases
Nov 10, 2023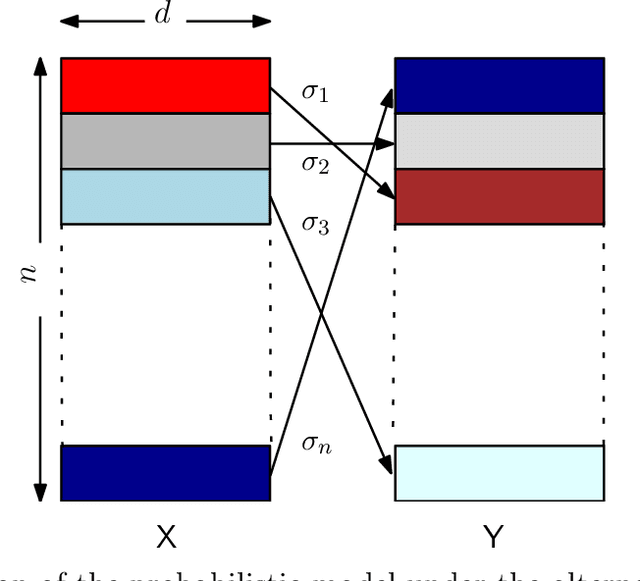
Abstract:In this paper, we investigate the problem of deciding whether two random databases $\mathsf{X}\in\mathcal{X}^{n\times d}$ and $\mathsf{Y}\in\mathcal{Y}^{n\times d}$ are statistically dependent or not. This is formulated as a hypothesis testing problem, where under the null hypothesis, these two databases are statistically independent, while under the alternative, there exists an unknown row permutation $\sigma$, such that $\mathsf{X}$ and $\mathsf{Y}^\sigma$, a permuted version of $\mathsf{Y}$, are statistically dependent with some known joint distribution, but have the same marginal distributions as the null. We characterize the thresholds at which optimal testing is information-theoretically impossible and possible, as a function of $n$, $d$, and some spectral properties of the generative distributions of the datasets. For example, we prove that if a certain function of the eigenvalues of the likelihood function and $d$, is below a certain threshold, as $d\to\infty$, then weak detection (performing slightly better than random guessing) is statistically impossible, no matter what the value of $n$ is. This mimics the performance of an efficient test that thresholds a centered version of the log-likelihood function of the observed matrices. We also analyze the case where $d$ is fixed, for which we derive strong (vanishing error) and weak detection lower and upper bounds.
Online Auditing of Information Flow
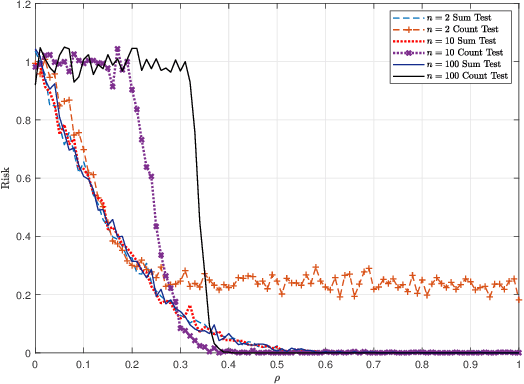
Oct 23, 2023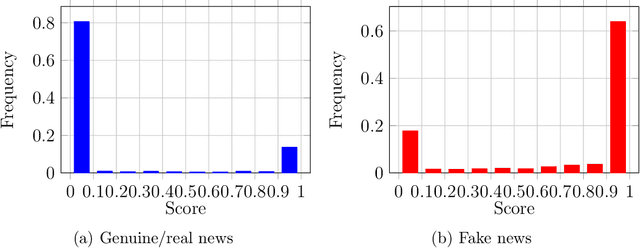

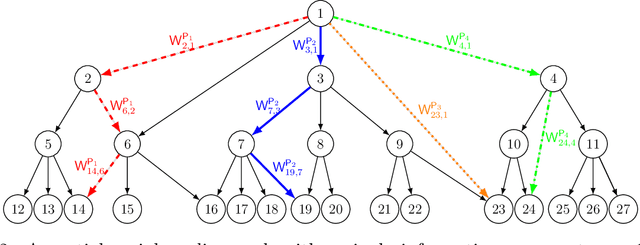
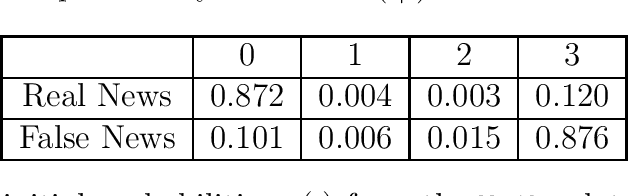
Abstract:Modern social media platforms play an important role in facilitating rapid dissemination of information through their massive user networks. Fake news, misinformation, and unverifiable facts on social media platforms propagate disharmony and affect society. In this paper, we consider the problem of online auditing of information flow/propagation with the goal of classifying news items as fake or genuine. Specifically, driven by experiential studies on real-world social media platforms, we propose a probabilistic Markovian information spread model over networks modeled by graphs. We then formulate our inference task as a certain sequential detection problem with the goal of minimizing the combination of the error probability and the time it takes to achieve correct decision. For this model, we find the optimal detection algorithm minimizing the aforementioned risk and prove several statistical guarantees. We then test our algorithm over real-world datasets. To that end, we first construct an offline algorithm for learning the probabilistic information spreading model, and then apply our optimal detection algorithm. Experimental study show that our algorithm outperforms state-of-the-art misinformation detection algorithms in terms of accuracy and detection time.
Deep Learning-Aided Subspace-Based DOA Recovery for Sparse Arrays
Sep 10, 2023Abstract:Sparse arrays enable resolving more direction of arrivals (DoAs) than antenna elements using non-uniform arrays. This is typically achieved by reconstructing the covariance of a virtual large uniform linear array (ULA), which is then processed by subspace DoA estimators. However, these method assume that the signals are non-coherent and the array is calibrated; the latter often challenging to achieve in sparse arrays, where one cannot access the virtual array elements. In this work, we propose Sparse-SubspaceNet, which leverages deep learning to enable subspace-based DoA recovery from sparse miscallibrated arrays with coherent sources. Sparse- SubspaceNet utilizes a dedicated deep network to learn from data how to compute a surrogate virtual array covariance that is divisible into distinguishable subspaces. By doing so, we learn to cope with coherent sources and miscalibrated sparse arrays, while preserving the interpretability and the suitability of model-based subspace DoA estimators.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge