AdaRankGrad: Adaptive Gradient-Rank and Moments for Memory-Efficient LLMs Training and Fine-Tuning
Paper and Code
Oct 23, 2024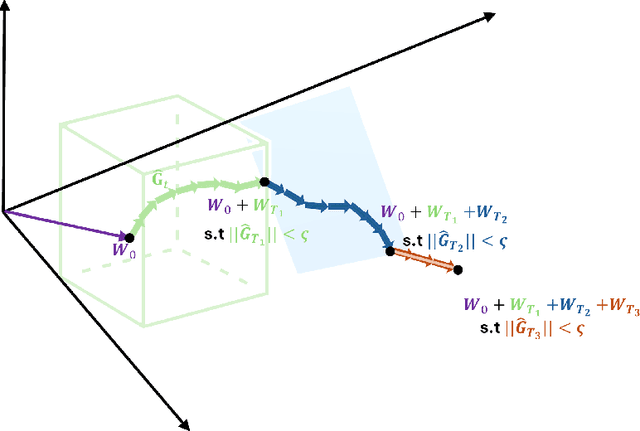
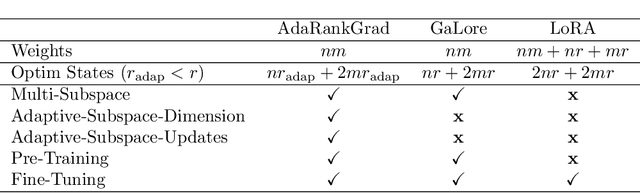
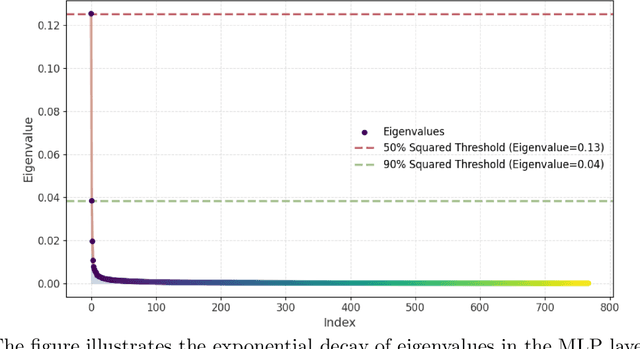

Training and fine-tuning large language models (LLMs) come with challenges related to memory and computational requirements due to the increasing size of the model weights and the optimizer states. Various techniques have been developed to tackle these challenges, such as low-rank adaptation (LoRA), which involves introducing a parallel trainable low-rank matrix to the fixed pre-trained weights at each layer. However, these methods often fall short compared to the full-rank weight training approach, as they restrict the parameter search to a low-rank subspace. This limitation can disrupt training dynamics and require a full-rank warm start to mitigate the impact. In this paper, we introduce a new method inspired by a phenomenon we formally prove: as training progresses, the rank of the estimated layer gradients gradually decreases, and asymptotically approaches rank one. Leveraging this, our approach involves adaptively reducing the rank of the gradients during Adam optimization steps, using an efficient online-updating low-rank projections rule. We further present a randomized SVD scheme for efficiently finding the projection matrix. Our technique enables full-parameter fine-tuning with adaptive low-rank gradient updates, significantly reducing overall memory requirements during training compared to state-of-the-art methods while improving model performance in both pretraining and fine-tuning. Finally, we provide a convergence analysis of our method and demonstrate its merits for training and fine-tuning language and biological foundation models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge