AdaRankGrad: Adaptive Gradient-Rank and Moments for Memory-Efficient LLMs Training and Fine-Tuning

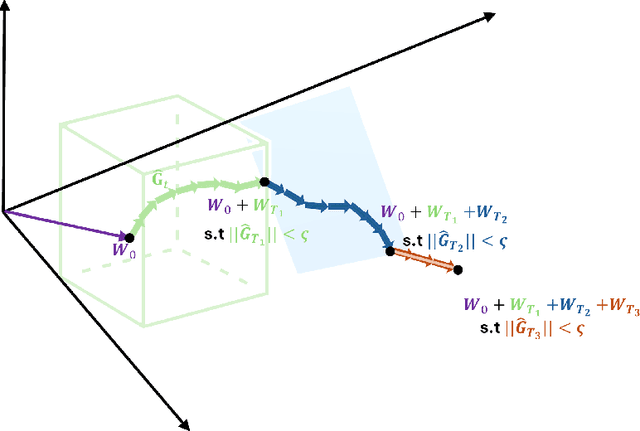
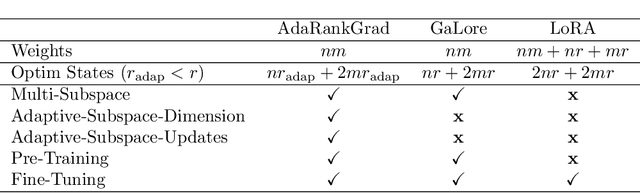
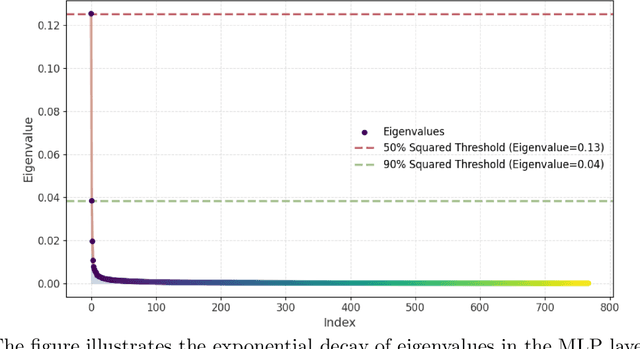
Training and fine-tuning large language models (LLMs) come with challenges related to memory and computational requirements due to the increasing size of the model weights and the optimizer states. Various techniques have been developed to tackle these challenges, such as low-rank adaptation (LoRA), which involves introducing a parallel trainable low-rank matrix to the fixed pre-trained weights at each layer. However, these methods often fall short compared to the full-rank weight training approach, as they restrict the parameter search to a low-rank subspace. This limitation can disrupt training dynamics and require a full-rank warm start to mitigate the impact. In this paper, we introduce a new method inspired by a phenomenon we formally prove: as training progresses, the rank of the estimated layer gradients gradually decreases, and asymptotically approaches rank one. Leveraging this, our approach involves adaptively reducing the rank of the gradients during Adam optimization steps, using an efficient online-updating low-rank projections rule. We further present a randomized SVD scheme for efficiently finding the projection matrix. Our technique enables full-parameter fine-tuning with adaptive low-rank gradient updates, significantly reducing overall memory requirements during training compared to state-of-the-art methods while improving model performance in both pretraining and fine-tuning. Finally, we provide a convergence analysis of our method and demonstrate its merits for training and fine-tuning language and biological foundation models.

Manifold Free Riemannian Optimization

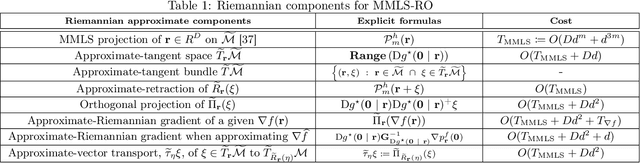
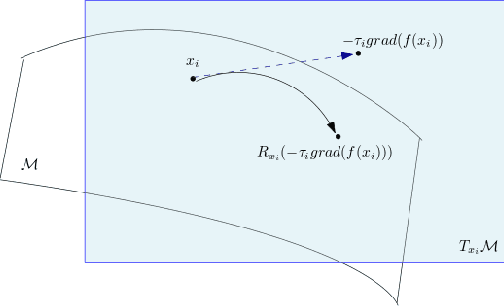
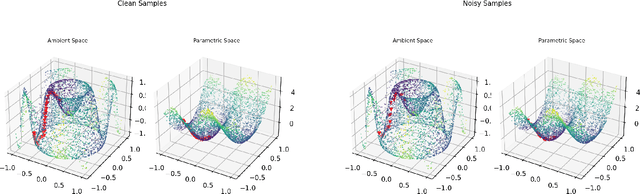
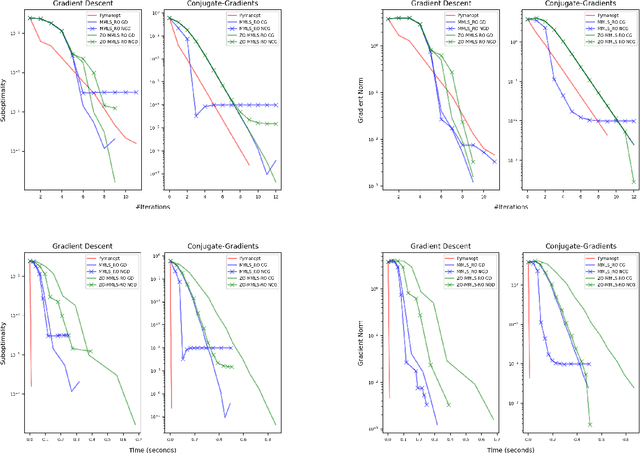
Riemannian optimization is a principled framework for solving optimization problems where the desired optimum is constrained to a smooth manifold $\mathcal{M}$. Algorithms designed in this framework usually require some geometrical description of the manifold, which typically includes tangent spaces, retractions, and gradients of the cost function. However, in many cases, only a subset (or none at all) of these elements can be accessed due to lack of information or intractability. In this paper, we propose a novel approach that can perform approximate Riemannian optimization in such cases, where the constraining manifold is a submanifold of $\R^{D}$. At the bare minimum, our method requires only a noiseless sample set of the cost function $(\x_{i}, y_{i})\in {\mathcal{M}} \times \mathbb{R}$ and the intrinsic dimension of the manifold $\mathcal{M}$. Using the samples, and utilizing the Manifold-MLS framework (Sober and Levin 2020), we construct approximations of the missing components entertaining provable guarantees and analyze their computational costs. In case some of the components are given analytically (e.g., if the cost function and its gradient are given explicitly, or if the tangent spaces can be computed), the algorithm can be easily adapted to use the accurate expressions instead of the approximations. We analyze the global convergence of Riemannian gradient-based methods using our approach, and we demonstrate empirically the strength of this method, together with a conjugate-gradients type method based upon similar principles.

Randomized Riemannian Preconditioning for Quadratically Constrained Problems

Optimization problem with quadratic equality constraints are prevalent in machine learning. Indeed, two important examples are Canonical Correlation Analysis (CCA) and Linear Discriminant Analysis (LDA). Unfortunately, methods for solving such problems typically involve computing matrix inverses and decomposition. For the aforementioned problems, these matrices are actually Gram matrices of input data matrices, and as such the computations are too expensive for large scale datasets. In this paper, we propose a sketching based approach for solving CCA and LDA that reduces the cost dependence on the input size. The proposed algorithms feature randomized preconditioning combined with Riemannian optimization.