Tamir Bendory
An Ultra-Fast MLE for Low SNR Multi-Reference Alignment
Jan 08, 2026Abstract:Motivated by single-particle cryo-electron microscopy, multi-reference alignment (MRA) models the task of recovering an unknown signal from multiple noisy observations corrupted by random rotations. The standard approach, expectation-maximization (EM), often becomes computationally prohibitive, particularly in low signal-to-noise ratio (SNR) settings. We introduce an alternative, ultra-fast algorithm for MRA over the special orthogonal group $\mathrm{SO}(2)$. By performing a Taylor expansion of the log-likelihood in the low-SNR regime, we estimate the signal by sequentially computing data-driven averages of observations. Our method requires only one pass over the data, dramatically reducing computational cost compared to EM. Numerical experiments show that the proposed approach achieves high accuracy in low-SNR environments and provides an excellent initialization for subsequent EM refinement.
Orbit recovery under the rigid motions group
Dec 08, 2025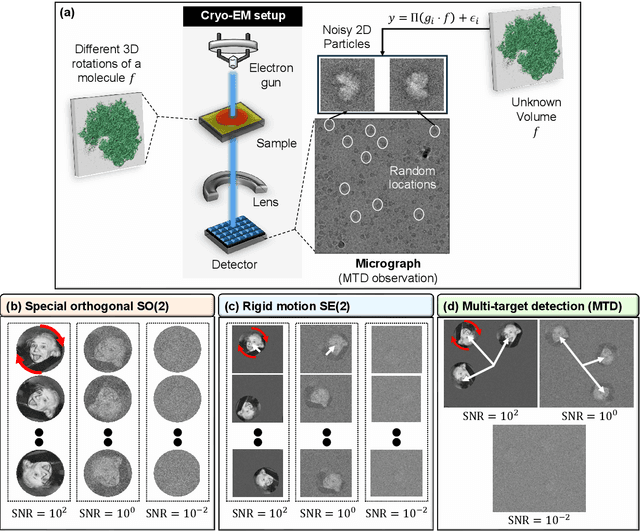


Abstract:We study the orbit recovery problem under the rigid-motion group SE(n), where the objective is to reconstruct an unknown signal from multiple noisy observations subjected to unknown rotations and translations. This problem is fundamental in signal processing, computer vision, and structural biology. Our main theoretical contribution is bounding the sample complexity of this problem. We show that if the d-th order moment under the rotation group SO(n) uniquely determines the signal orbit, then orbit recovery under SE(n) is achievable with $N\gtrsim σ^{2d+4}$ samples as the noise variance $σ^2 \to \infty$. The key technical insight is that the d-th order SO(n) moments can be explicitly recovered from (d+2)-order SE(n) autocorrelations, enabling us to transfer known results from the rotation-only setting to the rigid-motion case. We further harness this result to derive a matching bound to the sample complexity of the multi-target detection model that serves as an abstract framework for electron-microscopy-based technologies in structural biology, such as single-particle cryo-electron microscopy (cryo-EM) and cryo-electron tomography (cryo-ET). Beyond theory, we present a provable computational pipeline for rigid-motion orbit recovery in three dimensions. Starting from rigid-motion autocorrelations, we extract the SO(3) moments and demonstrate successful reconstruction of a 3-D macromolecular structure. Importantly, this algorithmic approach is valid at any noise level, suggesting that even very small macromolecules, long believed to be inaccessible using structural biology electron-microscopy-based technologies, may, in principle, be reconstructed given sufficient data.
SO(3)-invariant PCA with application to molecular data
Oct 21, 2025Abstract:Principal component analysis (PCA) is a fundamental technique for dimensionality reduction and denoising; however, its application to three-dimensional data with arbitrary orientations -- common in structural biology -- presents significant challenges. A naive approach requires augmenting the dataset with many rotated copies of each sample, incurring prohibitive computational costs. In this paper, we extend PCA to 3D volumetric datasets with unknown orientations by developing an efficient and principled framework for SO(3)-invariant PCA that implicitly accounts for all rotations without explicit data augmentation. By exploiting underlying algebraic structure, we demonstrate that the computation involves only the square root of the total number of covariance entries, resulting in a substantial reduction in complexity. We validate the method on real-world molecular datasets, demonstrating its effectiveness and opening up new possibilities for large-scale, high-dimensional reconstruction problems.
Expectation-maximization for multi-reference alignment: Two pitfalls and one remedy
May 27, 2025Abstract:We study the multi-reference alignment model, which involves recovering a signal from noisy observations that have been randomly transformed by an unknown group action, a fundamental challenge in statistical signal processing, computational imaging, and structural biology. While much of the theoretical literature has focused on the asymptotic sample complexity of this model, the practical performance of reconstruction algorithms, particularly of the omnipresent expectation maximization (EM) algorithm, remains poorly understood. In this work, we present a detailed investigation of EM in the challenging low signal-to-noise ratio (SNR) regime. We identify and characterize two failure modes that emerge in this setting. The first, called Einstein from Noise, reveals a strong sensitivity to initialization, with reconstructions resembling the input template regardless of the true underlying signal. The second phenomenon, referred to as the Ghost of Newton, involves EM initially converging towards the correct solution but later diverging, leading to a loss of reconstruction fidelity. We provide theoretical insights and support our findings through numerical experiments. Finally, we introduce a simple, yet effective modification to EM based on mini-batching, which mitigates the above artifacts. Supported by both theory and experiments, this mini-batching approach processes small data subsets per iteration, reducing initialization bias and computational cost, while maintaining accuracy comparable to full-batch EM.
The stability of generalized phase retrieval problem over compact groups
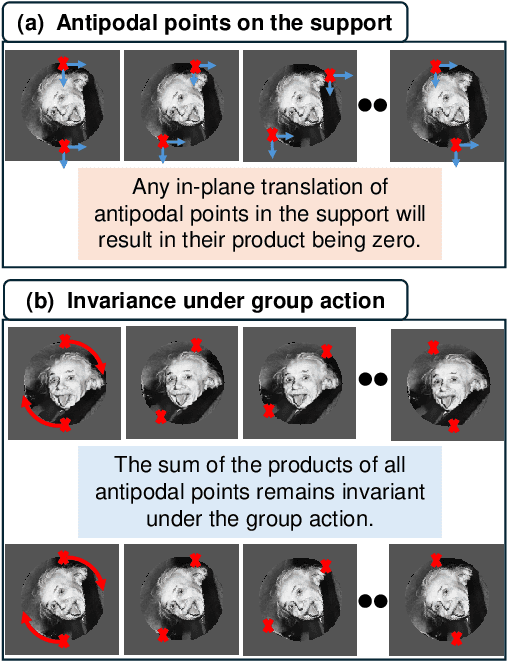
May 07, 2025
Abstract:The generalized phase retrieval problem over compact groups aims to recover a set of matrices, representing an unknown signal, from their associated Gram matrices, leveraging prior structural knowledge about the signal. This framework generalizes the classical phase retrieval problem, which reconstructs a signal from the magnitudes of its Fourier transform, to a richer setting involving non-abelian compact groups. In this broader context, the unknown phases in Fourier space are replaced by unknown orthogonal matrices that arise from the action of a compact group on a finite-dimensional vector space. This problem is primarily motivated by advances in electron microscopy to determining the 3D structure of biological macromolecules from highly noisy observations. To capture realistic assumptions from machine learning and signal processing, we model the signal as belonging to one of several broad structural families: a generic linear subspace, a sparse representation in a generic basis, the output of a generic ReLU neural network, or a generic low-dimensional manifold. Our main result shows that, under mild conditions, the generalized phase retrieval problem not only admits a unique solution (up to inherent group symmetries), but also satisfies a bi-Lipschitz property. This implies robustness to both noise and model mismatch, an essential requirement for practical use, especially when measurements are severely corrupted by noise. These findings provide theoretical support for a wide class of scientific problems under modern structural assumptions, and they offer strong foundations for developing robust algorithms in high-noise regimes.
A note on the sample complexity of multi-target detection
Jan 21, 2025Abstract:This work studies the sample complexity of the multi-target detection (MTD) problem, which involves recovering a signal from a noisy measurement containing multiple instances of a target signal in unknown locations, each transformed by a random group element. This problem is primarily motivated by single-particle cryo-electron microscopy (cryo-EM), a groundbreaking technology for determining the structures of biological molecules. We establish upper and lower bounds for various MTD models in the high-noise regime as a function of the group, the distribution over the group, and the arrangement of signal occurrences within the measurement. The lower bounds are established through a reduction to the related multi-reference alignment problem, while the upper bounds are derived from explicit recovery algorithms utilizing autocorrelation analysis. These findings provide fundamental insights into estimation limits in noisy environments and lay the groundwork for extending this analysis to more complex applications, such as cryo-EM.
The generalized phase retrieval problem over compact groups
Jan 07, 2025
Abstract:The classical phase retrieval problem involves estimating a signal from its Fourier magnitudes (power spectrum) by leveraging prior information about the desired signal. This paper extends the problem to compact groups, addressing the recovery of a set of matrices from their Gram matrices. In this broader context, the missing phases in Fourier space are replaced by missing unitary or orthogonal matrices arising from the action of a compact group on a finite-dimensional vector space. This generalization is driven by applications in multi-reference alignment and single-particle cryo-electron microscopy, a pivotal technology in structural biology. We define the generalized phase retrieval problem over compact groups and explore its underlying algebraic structure. We survey recent results on the uniqueness of solutions, focusing on the significant class of semialgebraic priors. Furthermore, we present a family of algorithms inspired by classical phase retrieval techniques. Finally, we propose a conjecture on the stability of the problem based on bi-Lipschitz analysis, supported by numerical experiments.
Confirmation Bias in Gaussian Mixture Models
Aug 19, 2024Abstract:Confirmation bias, the tendency to interpret information in a way that aligns with one's preconceptions, can profoundly impact scientific research, leading to conclusions that reflect the researcher's hypotheses even when the observational data do not support them. This issue is especially critical in scientific fields involving highly noisy observations, such as cryo-electron microscopy. This study investigates confirmation bias in Gaussian mixture models. We consider the following experiment: A team of scientists assumes they are analyzing data drawn from a Gaussian mixture model with known signals (hypotheses) as centroids. However, in reality, the observations consist entirely of noise without any informative structure. The researchers use a single iteration of the K-means or expectation-maximization algorithms, two popular algorithms to estimate the centroids. Despite the observations being pure noise, we show that these algorithms yield biased estimates that resemble the initial hypotheses, contradicting the unbiased expectation that averaging these noise observations would converge to zero. Namely, the algorithms generate estimates that mirror the postulated model, although the hypotheses (the presumed centroids of the Gaussian mixture) are not evident in the observations. Specifically, among other results, we prove a positive correlation between the estimates produced by the algorithms and the corresponding hypotheses. We also derive explicit closed-form expressions of the estimates for a finite and infinite number of hypotheses. This study underscores the risks of confirmation bias in low signal-to-noise environments, provides insights into potential pitfalls in scientific methodologies, and highlights the importance of prudent data interpretation.
Einstein from Noise: Statistical Analysis
Jul 07, 2024Abstract:``Einstein from noise" (EfN) is a prominent example of the model bias phenomenon: systematic errors in the statistical model that lead to erroneous but consistent estimates. In the EfN experiment, one falsely believes that a set of observations contains noisy, shifted copies of a template signal (e.g., an Einstein image), whereas in reality, it contains only pure noise observations. To estimate the signal, the observations are first aligned with the template using cross-correlation, and then averaged. Although the observations contain nothing but noise, it was recognized early on that this process produces a signal that resembles the template signal! This pitfall was at the heart of a central scientific controversy about validation techniques in structural biology. This paper provides a comprehensive statistical analysis of the EfN phenomenon above. We show that the Fourier phases of the EfN estimator (namely, the average of the aligned noise observations) converge to the Fourier phases of the template signal, explaining the observed structural similarity. Additionally, we prove that the convergence rate is inversely proportional to the number of noise observations and, in the high-dimensional regime, to the Fourier magnitudes of the template signal. Moreover, in the high-dimensional regime, the Fourier magnitudes converge to a scaled version of the template signal's Fourier magnitudes. This work not only deepens the theoretical understanding of the EfN phenomenon but also highlights potential pitfalls in template matching techniques and emphasizes the need for careful interpretation of noisy observations across disciplines in engineering, statistics, physics, and biology.
A transversality theorem for semi-algebraic sets with application to signal recovery from the second moment and cryo-EM
May 07, 2024Abstract:Semi-algebraic priors are ubiquitous in signal processing and machine learning. Prevalent examples include a) linear models where the signal lies in a low-dimensional subspace; b) sparse models where the signal can be represented by only a few coefficients under a suitable basis; and c) a large family of neural network generative models. In this paper, we prove a transversality theorem for semi-algebraic sets in orthogonal or unitary representations of groups: with a suitable dimension bound, a generic translate of any semi-algebraic set is transverse to the orbits of the group action. This, in turn, implies that if a signal lies in a low-dimensional semi-algebraic set, then it can be recovered uniquely from measurements that separate orbits. As an application, we consider the implications of the transversality theorem to the problem of recovering signals that are translated by random group actions from their second moment. As a special case, we discuss cryo-EM: a leading technology to constitute the spatial structure of biological molecules, which serves as our prime motivation. In particular, we derive explicit bounds for recovering a molecular structure from the second moment under a semi-algebraic prior and deduce information-theoretic implications. We also obtain information-theoretic bounds for three additional applications: factoring Gram matrices, multi-reference alignment, and phase retrieval. Finally, we deduce bounds for designing permutation invariant separators in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge