Score-based diffusion priors for multi-target detection

Multi-target detection (MTD) is the problem of estimating an image from a large, noisy measurement that contains randomly translated and rotated copies of the image. Motivated by the single-particle cryo-electron microscopy technology, we design data-driven diffusion priors for the MTD problem, derived from score-based stochastic differential equations models. We then integrate the prior into the approximate expectation-maximization algorithm. In particular, our method alternates between an expectation step that approximates the expected log-likelihood and a maximization step that balances the approximated log-likelihood with the learned log-prior. We show on two datasets that adding the data-driven prior substantially reduces the estimation error, in particular in high noise regimes.

A stochastic approximate expectation-maximization for structure determination directly from cryo-EM micrographs

A single-particle cryo-electron microscopy (cryo-EM) measurement, called a micrograph, consists of multiple two-dimensional tomographic projections of a three-dimensional molecular structure at unknown locations, taken under unknown viewing directions. All existing cryo-EM algorithmic pipelines first locate and extract the projection images, and then reconstruct the structure from the extracted images. However, if the molecular structure is small, the signal-to-noise ratio (SNR) of the data is very low, and thus accurate detection of projection images within the micrograph is challenging. Consequently, all standard techniques fail in low-SNR regimes. To recover molecular structures from measurements of low SNR, and in particular small molecular structures, we devise a stochastic approximate expectation-maximization algorithm to estimate the three-dimensional structure directly from the micrograph, bypassing locating the projection images. We corroborate our computational scheme with numerical experiments, and present successful structure recoveries from simulated noisy measurements.

An approximate expectation-maximization for two-dimensional multi-target detection

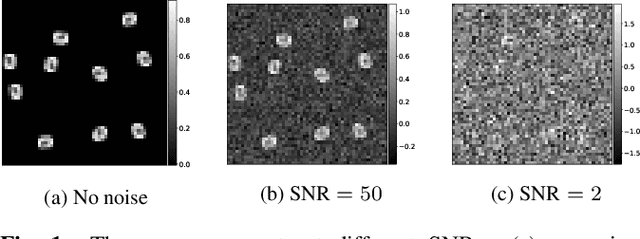
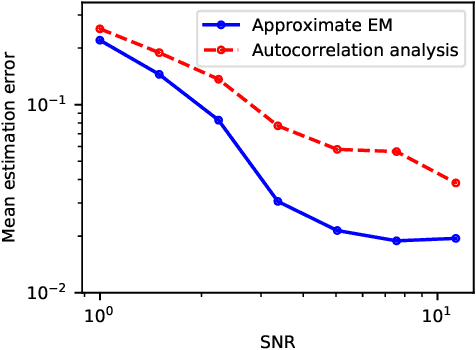
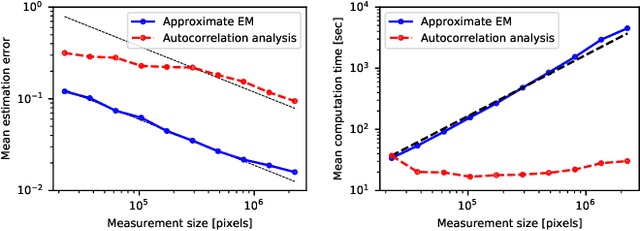
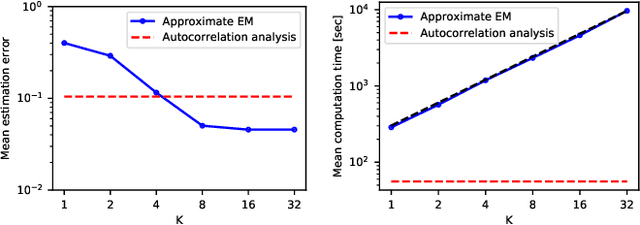
We consider the two-dimensional multi-target detection (MTD) problem of estimating a target image from a noisy measurement that contains multiple copies of the image, each randomly rotated and translated. The MTD model serves as a mathematical abstraction of the structure reconstruction problem in single-particle cryo-electron microscopy, the chief motivation of this study. We focus on high noise regimes, where accurate detection of image occurrences within a measurement is impossible. To estimate the image, we develop an expectation-maximization framework that aims to maximize an approximation of the likelihood function. We demonstrate image recovery in highly noisy environments, and show that our framework outperforms the previously studied autocorrelation analysis in a wide range of parameters. The code to reproduce all numerical experiments is publicly available at https://github.com/krshay/MTD-2D-EM.

Generalized autocorrelation analysis for multi-target detection

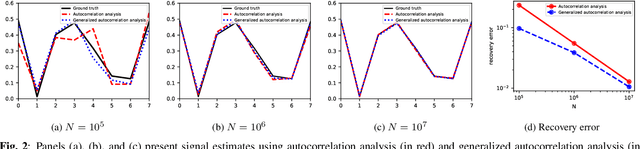
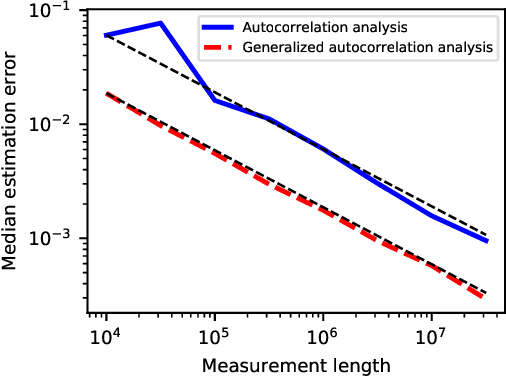
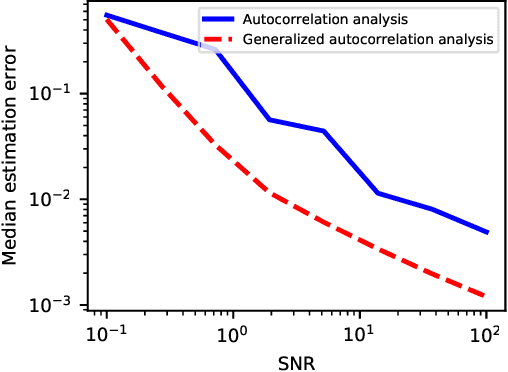
We study the multi-target detection problem of recovering a target signal from a noisy measurement that contains multiple copies of the signal at unknown locations. Motivated by the structure reconstruction problem in cryo-electron microscopy, we focus on the high noise regime, where noise hampers accurate detection of signal occurrences. Previous works proposed an autocorrelation analysis framework to estimate the signal directly from the measurement, without detecting signal occurrences. Specifically, autocorrelation analysis entails finding a signal that best matches the observable autocorrelations by minimizing a least squares objective. This paper extends this line of research by developing a generalized autocorrelation analysis framework that replaces the least squares by a weighted least squares. The optimal weights can be computed directly from the data and guarantee favorable statistical properties. We demonstrate signal recovery from highly noisy measurements, and show that the proposed framework outperforms autocorrelation analysis in a wide range of parameters.

Two-dimensional multi-target detection

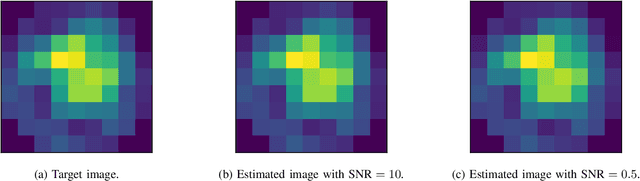
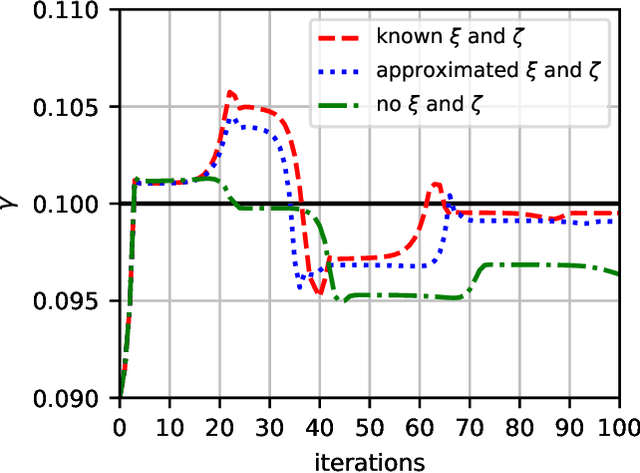
We consider the two-dimensional multi-target detection problem of recovering a target image from a noisy measurement that contains multiple copies of the image, each randomly rotated and translated. Motivated by the structure reconstruction problem in single-particle cryo-electron microscopy, we focus on the high noise regime, where the noise hampers accurate detection of the image occurrences. We develop an autocorrelation analysis framework to estimate the image directly from a measurement with an arbitrary spacing distribution of image occurrences, bypassing the estimation of individual locations and rotations. We conduct extensive numerical experiments, and demonstrate image recovery in highly noisy environments. The code to reproduce all numerical experiments is publicly available at https://github.com/krshay/MTD-2D.

Signal recovery from a few linear measurements of its high-order spectra

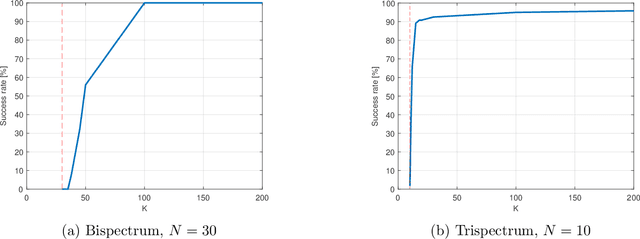
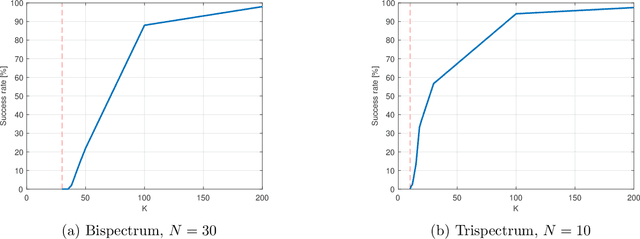
The $q$-th order spectrum is a polynomial of degree $q$ in the entries of a signal $x\in\mathbb{C}^N$, which is invariant under circular shifts of the signal. For $q\geq 3$, this polynomial determines the signal uniquely, up to a circular shift, and is called a high-order spectrum. The high-order spectra, and in particular the bispectrum ($q=3$) and the trispectrum ($q=4$), play a prominent role in various statistical signal processing and imaging applications, such as phase retrieval and single-particle reconstruction. However, the dimension of the $q$-th order spectrum is $N^{q-1}$, far exceeding the dimension of $x$, leading to increased computational load and storage requirements. In this work, we show that it is unnecessary to store and process the full high-order spectra: a signal can be characterized uniquely, up to a circular shift, from only $N+1$ linear measurements of its high-order spectra. The proof relies on tools from algebraic geometry and is corroborated by numerical experiments.