The stability of generalized phase retrieval problem over compact groups

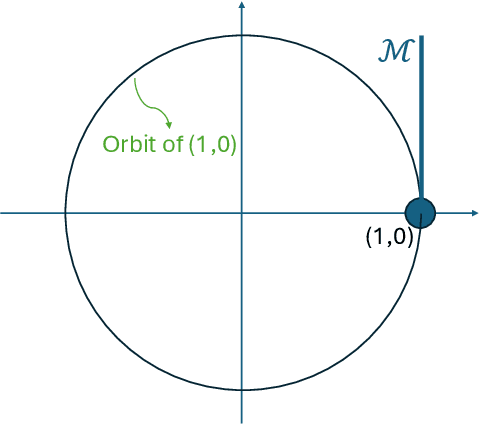
The generalized phase retrieval problem over compact groups aims to recover a set of matrices, representing an unknown signal, from their associated Gram matrices, leveraging prior structural knowledge about the signal. This framework generalizes the classical phase retrieval problem, which reconstructs a signal from the magnitudes of its Fourier transform, to a richer setting involving non-abelian compact groups. In this broader context, the unknown phases in Fourier space are replaced by unknown orthogonal matrices that arise from the action of a compact group on a finite-dimensional vector space. This problem is primarily motivated by advances in electron microscopy to determining the 3D structure of biological macromolecules from highly noisy observations. To capture realistic assumptions from machine learning and signal processing, we model the signal as belonging to one of several broad structural families: a generic linear subspace, a sparse representation in a generic basis, the output of a generic ReLU neural network, or a generic low-dimensional manifold. Our main result shows that, under mild conditions, the generalized phase retrieval problem not only admits a unique solution (up to inherent group symmetries), but also satisfies a bi-Lipschitz property. This implies robustness to both noise and model mismatch, an essential requirement for practical use, especially when measurements are severely corrupted by noise. These findings provide theoretical support for a wide class of scientific problems under modern structural assumptions, and they offer strong foundations for developing robust algorithms in high-noise regimes.

The generalized phase retrieval problem over compact groups

The classical phase retrieval problem involves estimating a signal from its Fourier magnitudes (power spectrum) by leveraging prior information about the desired signal. This paper extends the problem to compact groups, addressing the recovery of a set of matrices from their Gram matrices. In this broader context, the missing phases in Fourier space are replaced by missing unitary or orthogonal matrices arising from the action of a compact group on a finite-dimensional vector space. This generalization is driven by applications in multi-reference alignment and single-particle cryo-electron microscopy, a pivotal technology in structural biology. We define the generalized phase retrieval problem over compact groups and explore its underlying algebraic structure. We survey recent results on the uniqueness of solutions, focusing on the significant class of semialgebraic priors. Furthermore, we present a family of algorithms inspired by classical phase retrieval techniques. Finally, we propose a conjecture on the stability of the problem based on bi-Lipschitz analysis, supported by numerical experiments.

A transversality theorem for semi-algebraic sets with application to signal recovery from the second moment and cryo-EM

Semi-algebraic priors are ubiquitous in signal processing and machine learning. Prevalent examples include a) linear models where the signal lies in a low-dimensional subspace; b) sparse models where the signal can be represented by only a few coefficients under a suitable basis; and c) a large family of neural network generative models. In this paper, we prove a transversality theorem for semi-algebraic sets in orthogonal or unitary representations of groups: with a suitable dimension bound, a generic translate of any semi-algebraic set is transverse to the orbits of the group action. This, in turn, implies that if a signal lies in a low-dimensional semi-algebraic set, then it can be recovered uniquely from measurements that separate orbits. As an application, we consider the implications of the transversality theorem to the problem of recovering signals that are translated by random group actions from their second moment. As a special case, we discuss cryo-EM: a leading technology to constitute the spatial structure of biological molecules, which serves as our prime motivation. In particular, we derive explicit bounds for recovering a molecular structure from the second moment under a semi-algebraic prior and deduce information-theoretic implications. We also obtain information-theoretic bounds for three additional applications: factoring Gram matrices, multi-reference alignment, and phase retrieval. Finally, we deduce bounds for designing permutation invariant separators in machine learning.

The beltway problem over orthogonal groups

The classical beltway problem entails recovering a set of points from their unordered pairwise distances on the circle. This problem can be viewed as a special case of the crystallographic phase retrieval problem of recovering a sparse signal from its periodic autocorrelation. Based on this interpretation, and motivated by cryo-electron microscopy, we suggest a natural generalization to orthogonal groups: recovering a sparse signal, up to an orthogonal transformation, from its autocorrelation over the orthogonal group. If the support of the signal is collision-free, we bound the number of solutions to the beltway problem over orthogonal groups, and prove that this bound is exactly one when the support of the signal is radially collision-free (i.e., the support points have distinct magnitudes). We also prove that if the pairwise products of the signal's weights are distinct, then the autocorrelation determines the signal uniquely, up to an orthogonal transformation. We conclude the paper by considering binary signals and show that in this case, the collision-free condition need not be sufficient to determine signals up to orthogonal transformation.

Phase retrieval with semi-algebraic and ReLU neural network priors

The key ingredient to retrieving a signal from its Fourier magnitudes, namely, to solve the phase retrieval problem, is an effective prior on the sought signal. In this paper, we study the phase retrieval problem under the prior that the signal lies in a semi-algebraic set. This is a very general prior as semi-algebraic sets include linear models, sparse models, and ReLU neural network generative models. The latter is the main motivation of this paper, due to the remarkable success of deep generative models in a variety of imaging tasks, including phase retrieval. We prove that almost all signals in R^N can be determined from their Fourier magnitudes, up to a sign, if they lie in a (generic) semi-algebraic set of dimension N/2. The same is true for all signals if the semi-algebraic set is of dimension N/4. We also generalize these results to the problem of signal recovery from the second moment in multi-reference alignment models with multiplicity free representations of compact groups. This general result is then used to derive improved sample complexity bounds for recovering band-limited functions on the sphere from their noisy copies, each acted upon by a random element of SO(3).

Finite alphabet phase retrieval

We consider the finite alphabet phase retrieval problem: recovering a signal whose entries lie in a small alphabet of possible values from its Fourier magnitudes. This problem arises in the celebrated technology of X-ray crystallography to determine the atomic structure of biological molecules. Our main result states that for generic values of the alphabet, two signals have the same Fourier magnitudes if and only if several partitions have the same difference sets. Thus, the finite alphabet phase retrieval problem reduces to the combinatorial problem of determining a signal from those difference sets. Notably, this result holds true when one of the letters of the alphabet is zero, namely, for sparse signals with finite alphabet, which is the situation in X-ray crystallography.

The sample complexity of sparse multi-reference alignment and single-particle cryo-electron microscopy

Multi-reference alignment (MRA) is the problem of recovering a signal from its multiple noisy copies, each acted upon by a random group element. MRA is mainly motivated by single-particle cryo-electron microscopy (cryo-EM) that has recently joined X-ray crystallography as one of the two leading technologies to reconstruct biological molecular structures. Previous papers have shown that in the high noise regime, the sample complexity of MRA and cryo-EM is $n=\omega(\sigma^{2d})$, where $n$ is the number of observations, $\sigma^2$ is the variance of the noise, and $d$ is the lowest-order moment of the observations that uniquely determines the signal. In particular, it was shown that in many cases, $d=3$ for generic signals, and thus the sample complexity is $n=\omega(\sigma^6)$. In this paper, we analyze the second moment of the MRA and cryo-EM models. First, we show that in both models the second moment determines the signal up to a set of unitary matrices, whose dimension is governed by the decomposition of the space of signals into irreducible representations of the group. Second, we derive sparsity conditions under which a signal can be recovered from the second moment, implying sample complexity of $n=\omega(\sigma^4)$. Notably, we show that the sample complexity of cryo-EM is $n=\omega(\sigma^4)$ if at most one third of the coefficients representing the molecular structure are non-zero; this bound is near-optimal. The analysis is based on tools from representation theory and algebraic geometry. We also derive bounds on recovering a sparse signal from its power spectrum, which is the main computational problem of X-ray crystallography.

Algebraic theory of phase retrieval

The purpose of this article is to discuss recent advances in the growing field of phase retrieval, and to publicize open problems that we believe will be of interest to mathematicians in general, and algebraists in particular.

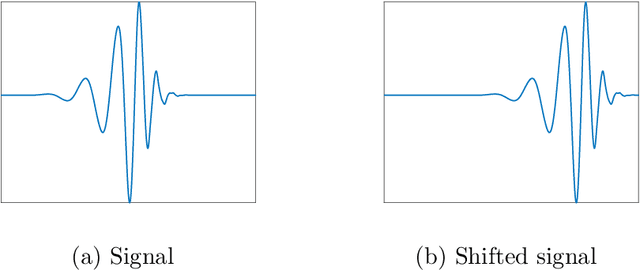
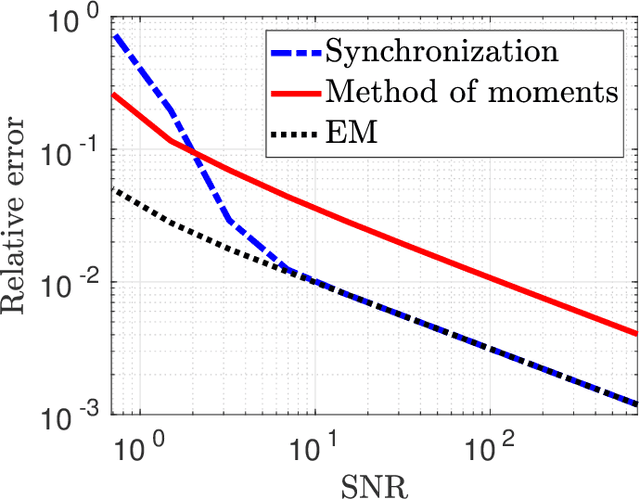
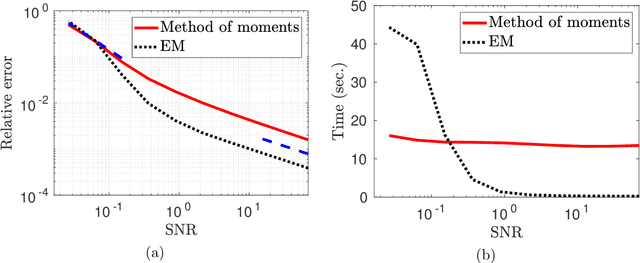
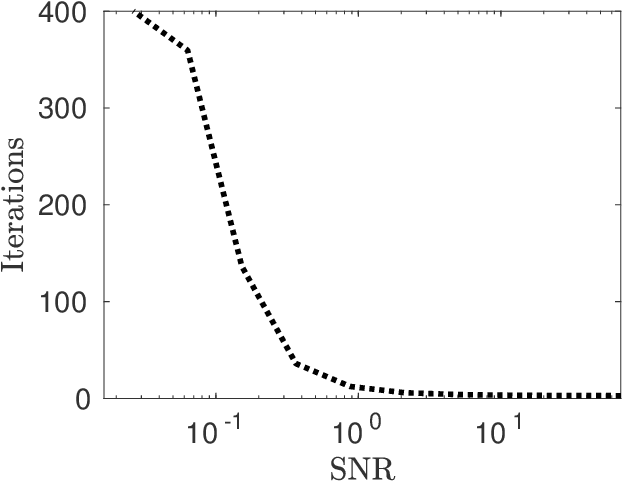
Dihedral multi-reference alignment

We study the dihedral multi-reference alignment problem of estimating the orbit of a signal from multiple noisy observations of the signal, translated by random elements of the dihedral group. We show that if the group elements are drawn from a generic distribution, the orbit of a generic signal is uniquely determined from the second moment of the observations. This implies that the optimal estimation rate in the high noise regime is proportional to the square of the variance of the noise. This is the first result of this type for multi-reference alignment over a non-abelian group with a non-uniform distribution of group elements. Based on tools from invariant theory and algebraic geometry, we also delineate conditions for unique orbit recovery for multi-reference alignment models over finite groups (namely, when the dihedral group is replaced by a general finite group) when the group elements are drawn from a generic distribution. Finally, we design and study numerically three computational frameworks for estimating the signal based on group synchronization, expectation-maximization, and the method of moments.

Signal recovery from a few linear measurements of its high-order spectra

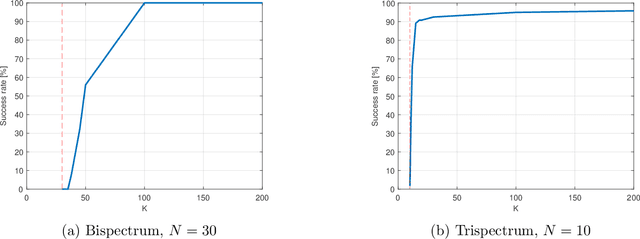
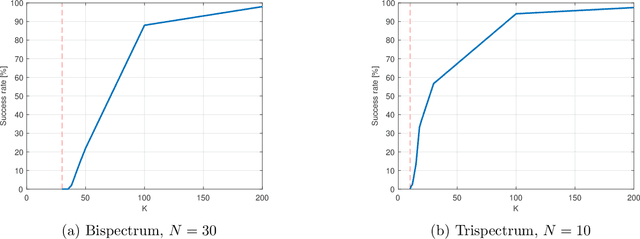
The $q$-th order spectrum is a polynomial of degree $q$ in the entries of a signal $x\in\mathbb{C}^N$, which is invariant under circular shifts of the signal. For $q\geq 3$, this polynomial determines the signal uniquely, up to a circular shift, and is called a high-order spectrum. The high-order spectra, and in particular the bispectrum ($q=3$) and the trispectrum ($q=4$), play a prominent role in various statistical signal processing and imaging applications, such as phase retrieval and single-particle reconstruction. However, the dimension of the $q$-th order spectrum is $N^{q-1}$, far exceeding the dimension of $x$, leading to increased computational load and storage requirements. In this work, we show that it is unnecessary to store and process the full high-order spectra: a signal can be characterized uniquely, up to a circular shift, from only $N+1$ linear measurements of its high-order spectra. The proof relies on tools from algebraic geometry and is corroborated by numerical experiments.