Tal Amir
The stability of generalized phase retrieval problem over compact groups
May 07, 2025
Abstract:The generalized phase retrieval problem over compact groups aims to recover a set of matrices, representing an unknown signal, from their associated Gram matrices, leveraging prior structural knowledge about the signal. This framework generalizes the classical phase retrieval problem, which reconstructs a signal from the magnitudes of its Fourier transform, to a richer setting involving non-abelian compact groups. In this broader context, the unknown phases in Fourier space are replaced by unknown orthogonal matrices that arise from the action of a compact group on a finite-dimensional vector space. This problem is primarily motivated by advances in electron microscopy to determining the 3D structure of biological macromolecules from highly noisy observations. To capture realistic assumptions from machine learning and signal processing, we model the signal as belonging to one of several broad structural families: a generic linear subspace, a sparse representation in a generic basis, the output of a generic ReLU neural network, or a generic low-dimensional manifold. Our main result shows that, under mild conditions, the generalized phase retrieval problem not only admits a unique solution (up to inherent group symmetries), but also satisfies a bi-Lipschitz property. This implies robustness to both noise and model mismatch, an essential requirement for practical use, especially when measurements are severely corrupted by noise. These findings provide theoretical support for a wide class of scientific problems under modern structural assumptions, and they offer strong foundations for developing robust algorithms in high-noise regimes.
Fourier Sliced-Wasserstein Embedding for Multisets and Measures
Apr 03, 2025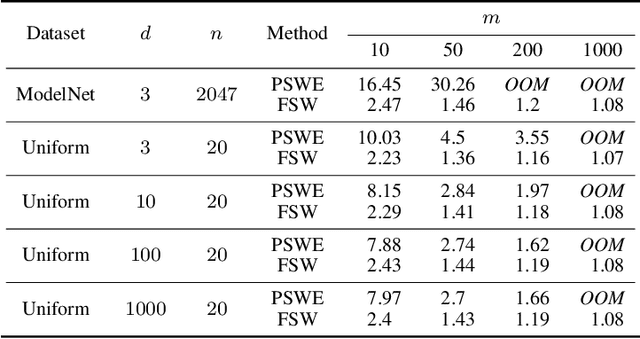
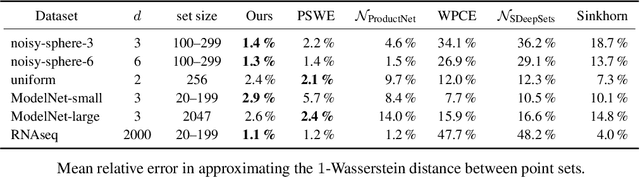
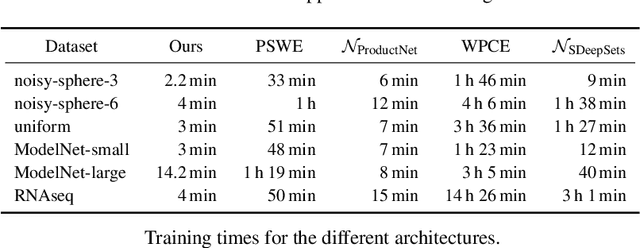
Abstract:We present the Fourier Sliced-Wasserstein (FSW) embedding - a novel method to embed multisets and measures over $\mathbb{R}^d$ into Euclidean space. Our proposed embedding approximately preserves the sliced Wasserstein distance on distributions, thereby yielding geometrically meaningful representations that better capture the structure of the input. Moreover, it is injective on measures and bi-Lipschitz on multisets - a significant advantage over prevalent methods based on sum- or max-pooling, which are provably not bi-Lipschitz, and, in many cases, not even injective. The required output dimension for these guarantees is near-optimal: roughly $2 N d$, where $N$ is the maximal input multiset size. Furthermore, we prove that it is impossible to embed distributions over $\mathbb{R}^d$ into Euclidean space in a bi-Lipschitz manner. Thus, the metric properties of our embedding are, in a sense, the best possible. Through numerical experiments, we demonstrate that our method yields superior multiset representations that improve performance in practical learning tasks. Specifically, we show that (a) a simple combination of the FSW embedding with an MLP achieves state-of-the-art performance in learning the (non-sliced) Wasserstein distance; and (b) replacing max-pooling with the FSW embedding makes PointNet significantly more robust to parameter reduction, with only minor performance degradation even after a 40-fold reduction.
FSW-GNN: A Bi-Lipschitz WL-Equivalent Graph Neural Network
Oct 10, 2024Abstract:Many of the most popular graph neural networks fall into the category of message-passing neural networks (MPNNs). Famously, MPNNs' ability to distinguish between graphs is limited to graphs separable by the Weisfeiler-Lemann (WL) graph isomorphism test, and the strongest MPNNs, in terms of separation power, are WL-equivalent. Recently, it was shown that the quality of separation provided by standard WL-equivalent MPNN can be very low, resulting in WL-separable graphs being mapped to very similar, hardly distinguishable features. This paper addresses this issue by seeking bi-Lipschitz continuity guarantees for MPNNs. We demonstrate that, in contrast with standard summation-based MPNNs, which lack bi-Lipschitz properties, our proposed model provides a bi-Lipschitz graph embedding with respect to two standard graph metrics. Empirically, we show that our MPNN is competitive with standard MPNNs for several graph learning tasks and is far more accurate in over-squashing long-range tasks.
Injective Sliced-Wasserstein embedding for weighted sets and point clouds
May 26, 2024


Abstract:We present the $\textit{Sliced Wasserstein Embedding}$ $\unicode{x2014}$ a novel method to embed multisets and distributions over $\mathbb{R}^d$ into Euclidean space. Our embedding is injective and approximately preserves the Sliced Wasserstein distance. Moreover, when restricted to multisets, it is bi-Lipschitz. We also prove that it is $\textit{impossible}$ to embed distributions over $\mathbb{R}^d$ into a Euclidean space in a bi-Lipschitz manner, even under the assumption that their support is bounded and finite. We demonstrate empirically that our embedding offers practical advantage in learning tasks over existing methods for handling multisets.
Weisfeiler Leman for Euclidean Equivariant Machine Learning
Feb 04, 2024



Abstract:The $k$-Weifeiler-Leman ($k$-WL) graph isomorphism test hierarchy is a common method for assessing the expressive power of graph neural networks (GNNs). Recently, the $2$-WL test was proven to be complete on weighted graphs which encode $3\mathrm{D}$ point cloud data. Consequently, GNNs whose expressive power is equivalent to the $2$-WL test are provably universal on point clouds. Yet, this result is limited to invariant continuous functions on point clouds. In this paper we extend this result in three ways: Firstly, we show that $2$-WL tests can be extended to point clouds which include both positions and velocity, a scenario often encountered in applications. Secondly, we show that PPGN (Maron et al., 2019) can simulate $2$-WL uniformly on all point clouds with low complexity. Finally, we show that a simple modification of this PPGN architecture can be used to obtain a universal equivariant architecture that can approximate all continuous equivariant functions uniformly. Building on our results, we develop our WeLNet architecture, which can process position-velocity pairs, compute functions fully equivariant to permutations and rigid motions, and is provably complete and universal. Remarkably, WeLNet is provably complete precisely in the setting in which it is implemented in practice. Our theoretical results are complemented by experiments showing WeLNet sets new state-of-the-art results on the N-Body dynamics task and the GEOM-QM9 molecular conformation generation task.
Neural Injective Functions for Multisets, Measures and Graphs via a Finite Witness Theorem
Jun 10, 2023



Abstract:Injective multiset functions have a key role in the theoretical study of machine learning on multisets and graphs. Yet, there remains a gap between the provably injective multiset functions considered in theory, which typically rely on polynomial moments, and the multiset functions used in practice which typically rely on $\textit{neural moments}$, whose injectivity on multisets has not been studied to date. In this paper we bridge this gap by showing that moments of neural network do define an injective multiset function, provided that an analytic non-polynomial activation is used. The number of moments required by our theory is optimal up to a multiplicative factor of two. To prove this result, we state and prove a $\textit{finite witness theorem}$, which is of independent interest. As a corollary to our main theorem, we derive new approximation results for functions on multisets and measures, and new separation results for graph neural networks. We also provide two negative results: We show that (1) moments of piecewise-linear neural networks do not lead to injective multiset functions, and (2) even when moment-based multiset functions are injective, they will never be bi-Lipschitz.
Complete Neural Networks for Euclidean Graphs
Feb 01, 2023
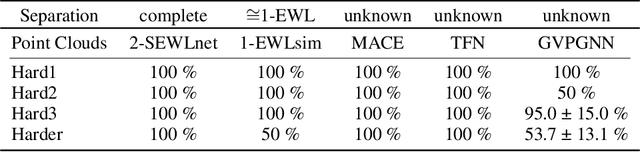

Abstract:We propose a 2-WL-like geometric graph isomorphism test and prove it is complete when applied to Euclidean Graphs in $\mathbb{R}^3$. We then use recent results on multiset embeddings to devise an efficient geometric GNN model with equivalent separation power. We verify empirically that our GNN model is able to separate particularly challenging synthetic examples, and demonstrate its usefulness for a chemical property prediction problem.
Symmetrized Robust Procrustes: Constant-Factor Approximation and Exact Recovery
Jul 18, 2022



Abstract:The classical $\textit{Procrustes}$ problem is to find a rigid motion (orthogonal transformation and translation) that best aligns two given point-sets in the least-squares sense. The $\textit{Robust Procrustes}$ problem is an important variant, in which a power-1 objective is used instead of least squares to improve robustness to outliers. While the optimal solution of the least-squares problem can be easily computed in closed form, dating back to Sch\"onemann (1966), no such solution is known for the power-1 problem. In this paper we propose a novel convex relaxation for the Robust Procrustes problem. Our relaxation enjoys several theoretical and practical advantages: Theoretically, we prove that our method provides a $\sqrt{2}$-factor approximation to the Robust Procrustes problem, and that, under appropriate assumptions, it exactly recovers the true rigid motion from point correspondences contaminated by outliers. In practice, we find in numerical experiments on both synthetic and real robust Procrustes problems, that our method performs similarly to the standard Iteratively Reweighted Least Squares (IRLS). However the convexity of our algorithm allows incorporating additional convex penalties, which are not readily amenable to IRLS. This turns out to be a substantial advantage, leading to improved results in high-dimensional problems, including non-rigid shape alignment and semi-supervised interlingual word translation.
The Trimmed Lasso: Sparse Recovery Guarantees and Practical Optimization by the Generalized Soft-Min Penalty
May 18, 2020



Abstract:We present a new approach to solve the sparse approximation or best subset selection problem, namely find a $k$-sparse vector ${\bf x}\in\mathbb{R}^d$ that minimizes the $\ell_2$ residual $\lVert A{\bf x}-{\bf y} \rVert_2$. We consider a regularized approach, whereby this residual is penalized by the non-convex $\textit{trimmed lasso}$, defined as the $\ell_1$-norm of ${\bf x}$ excluding its $k$ largest-magnitude entries. We prove that the trimmed lasso has several appealing theoretical properties, and in particular derive sparse recovery guarantees assuming successful optimization of the penalized objective. Next, we show empirically that directly optimizing this objective can be quite challenging. Instead, we propose a surrogate for the trimmed lasso, called the $\textit{generalized soft-min}$. This penalty smoothly interpolates between the classical lasso and the trimmed lasso, while taking into account all possible $k$-sparse patterns. The generalized soft-min penalty involves summation over $\binom{d}{k}$ terms, yet we derive a polynomial-time algorithm to compute it. This, in turn, yields a practical method for the original sparse approximation problem. Via simulations, we demonstrate its competitive performance compared to current state of the art.
A New Rank Constraint on Multi-view Fundamental Matrices, and its Application to Camera Location Recovery
Feb 10, 2017



Abstract:Accurate estimation of camera matrices is an important step in structure from motion algorithms. In this paper we introduce a novel rank constraint on collections of fundamental matrices in multi-view settings. We show that in general, with the selection of proper scale factors, a matrix formed by stacking fundamental matrices between pairs of images has rank 6. Moreover, this matrix forms the symmetric part of a rank 3 matrix whose factors relate directly to the corresponding camera matrices. We use this new characterization to produce better estimations of fundamental matrices by optimizing an L1-cost function using Iterative Re-weighted Least Squares and Alternate Direction Method of Multiplier. We further show that this procedure can improve the recovery of camera locations, particularly in multi-view settings in which fewer images are available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge