Semi-Supervised Sparse Gaussian Classification: Provable Benefits of Unlabeled Data

The premise of semi-supervised learning (SSL) is that combining labeled and unlabeled data yields significantly more accurate models. Despite empirical successes, the theoretical understanding of SSL is still far from complete. In this work, we study SSL for high dimensional sparse Gaussian classification. To construct an accurate classifier a key task is feature selection, detecting the few variables that separate the two classes. % For this SSL setting, we analyze information theoretic lower bounds for accurate feature selection as well as computational lower bounds, assuming the low-degree likelihood hardness conjecture. % Our key contribution is the identification of a regime in the problem parameters (dimension, sparsity, number of labeled and unlabeled samples) where SSL is guaranteed to be advantageous for classification. Specifically, there is a regime where it is possible to construct in polynomial time an accurate SSL classifier. However, % any computationally efficient supervised or unsupervised learning schemes, that separately use only the labeled or unlabeled data would fail. Our work highlights the provable benefits of combining labeled and unlabeled data for {classification and} feature selection in high dimensions. We present simulations that complement our theoretical analysis.

A Majorization-Minimization Gauss-Newton Method for 1-Bit Matrix Completion

In 1-bit matrix completion, the aim is to estimate an underlying low-rank matrix from a partial set of binary observations. We propose a novel method for 1-bit matrix completion called MMGN. Our method is based on the majorization-minimization (MM) principle, which yields a sequence of standard low-rank matrix completion problems in our setting. We solve each of these sub-problems by a factorization approach that explicitly enforces the assumed low-rank structure and then apply a Gauss-Newton method. Our numerical studies and application to a real-data example illustrate that MMGN outputs comparable if not more accurate estimates, is often significantly faster, and is less sensitive to the spikiness of the underlying matrix than existing methods.

Imbalanced Mixed Linear Regression

We consider the problem of mixed linear regression (MLR), where each observed sample belongs to one of $K$ unknown linear models. In practical applications, the proportions of the $K$ components are often imbalanced. Unfortunately, most MLR methods do not perform well in such settings. Motivated by this practical challenge, in this work we propose Mix-IRLS, a novel, simple and fast algorithm for MLR with excellent performance on both balanced and imbalanced mixtures. In contrast to popular approaches that recover the $K$ models simultaneously, Mix-IRLS does it sequentially using tools from robust regression. Empirically, Mix-IRLS succeeds in a broad range of settings where other methods fail. These include imbalanced mixtures, small sample sizes, presence of outliers, and an unknown number of models $K$. In addition, Mix-IRLS outperforms competing methods on several real-world datasets, in some cases by a large margin. We complement our empirical results by deriving a recovery guarantee for Mix-IRLS, which highlights its advantage on imbalanced mixtures.

Distributed Sparse Linear Regression under Communication Constraints

In multiple domains, statistical tasks are performed in distributed settings, with data split among several end machines that are connected to a fusion center. In various applications, the end machines have limited bandwidth and power, and thus a tight communication budget. In this work we focus on distributed learning of a sparse linear regression model, under severe communication constraints. We propose several two round distributed schemes, whose communication per machine is sublinear in the data dimension. In our schemes, individual machines compute debiased lasso estimators, but send to the fusion center only very few values. On the theoretical front, we analyze one of these schemes and prove that with high probability it achieves exact support recovery at low signal to noise ratios, where individual machines fail to recover the support. We show in simulations that our scheme works as well as, and in some cases better, than more communication intensive approaches.

Distributed Sparse Linear Regression with Sublinear Communication

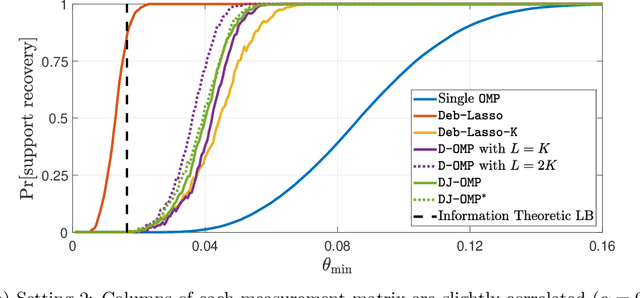
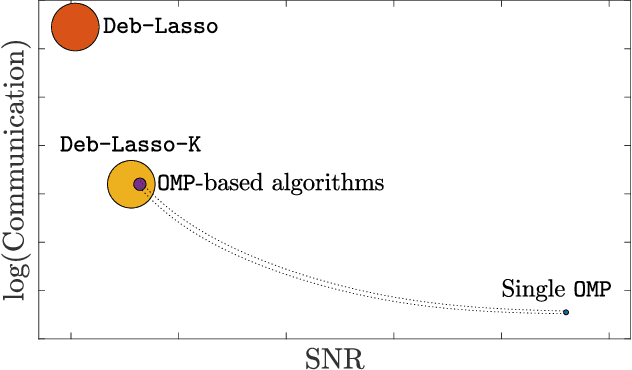
We study the problem of high-dimensional sparse linear regression in a distributed setting under both computational and communication constraints. Specifically, we consider a star topology network whereby several machines are connected to a fusion center, with whom they can exchange relatively short messages. Each machine holds noisy samples from a linear regression model with the same unknown sparse $d$-dimensional vector of regression coefficients $\theta$. The goal of the fusion center is to estimate the vector $\theta$ and its support using few computations and limited communication at each machine. In this work, we consider distributed algorithms based on Orthogonal Matching Pursuit (OMP) and theoretically study their ability to exactly recover the support of $\theta$. We prove that under certain conditions, even at low signal-to-noise-ratios where individual machines are unable to detect the support of $\theta$, distributed-OMP methods correctly recover it with total communication sublinear in $d$. In addition, we present simulations that illustrate the performance of distributed OMP-based algorithms and show that they perform similarly to more sophisticated and computationally intensive methods, and in some cases even outperform them.

Inductive Matrix Completion: No Bad Local Minima and a Fast Algorithm

The inductive matrix completion (IMC) problem is to recover a low rank matrix from few observed entries while incorporating prior knowledge about its row and column subspaces. In this work, we make three contributions to the IMC problem: (i) we prove that under suitable conditions, the IMC optimization landscape has no bad local minima; (ii) we derive a simple scheme with theoretical guarantees to estimate the rank of the unknown matrix; and (iii) we propose GNIMC, a simple Gauss-Newton based method to solve the IMC problem, analyze its runtime and derive recovery guarantees for it. The guarantees for GNIMC are sharper in several aspects than those available for other methods, including a quadratic convergence rate, fewer required observed entries and stability to errors or deviations from low-rank. Empirically, given entries observed uniformly at random, GNIMC recovers the underlying matrix substantially faster than several competing methods.

GNMR: A provable one-line algorithm for low rank matrix recovery

Low rank matrix recovery problems, including matrix completion and matrix sensing, appear in a broad range of applications. In this work we present GNMR -- an extremely simple iterative algorithm for low rank matrix recovery, based on a Gauss-Newton linearization. On the theoretical front, we derive recovery guarantees for GNMR in both the matrix sensing and matrix completion settings. A key property of GNMR is that it implicitly keeps the factor matrices approximately balanced throughout its iterations. On the empirical front, we show that for matrix completion with uniform sampling, GNMR performs better than several popular methods, especially when given very few observations close to the information limit.

Spectral Top-Down Recovery of Latent Tree Models

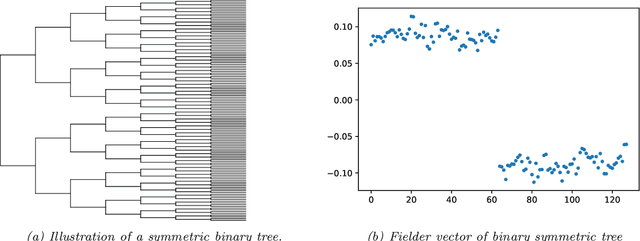
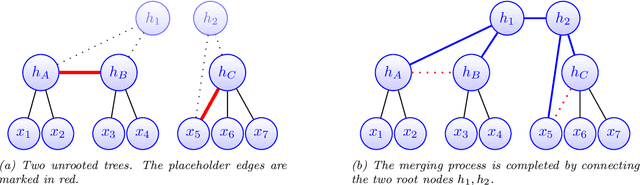
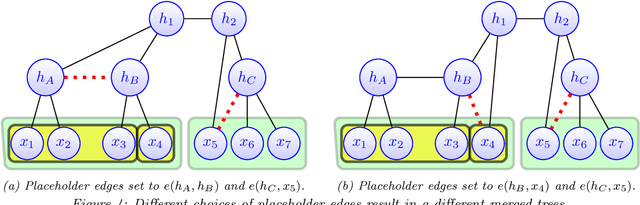
Modeling the distribution of high dimensional data by a latent tree graphical model is a common approach in multiple scientific domains. A common task is to infer the underlying tree structure given only observations of the terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, recover the structure separately for multiple randomly selected subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop Spectral Top-Down Recovery (STDR), a divide-and-conquer approach for inference of large latent tree models. Unlike previous methods, STDR's partitioning step is non-random. Instead, it is based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions this partitioning is consistent with the tree structure. This, in turn leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent, and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.

Sparse Normal Means Estimation with Sublinear Communication

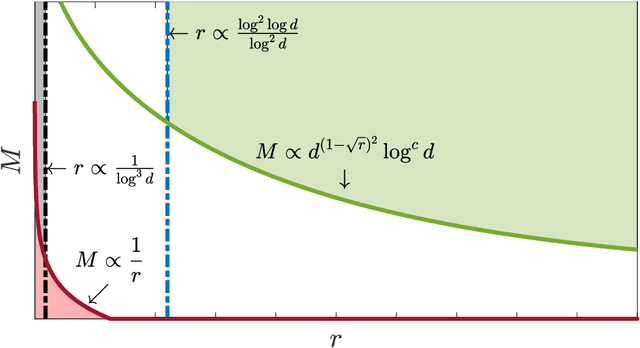
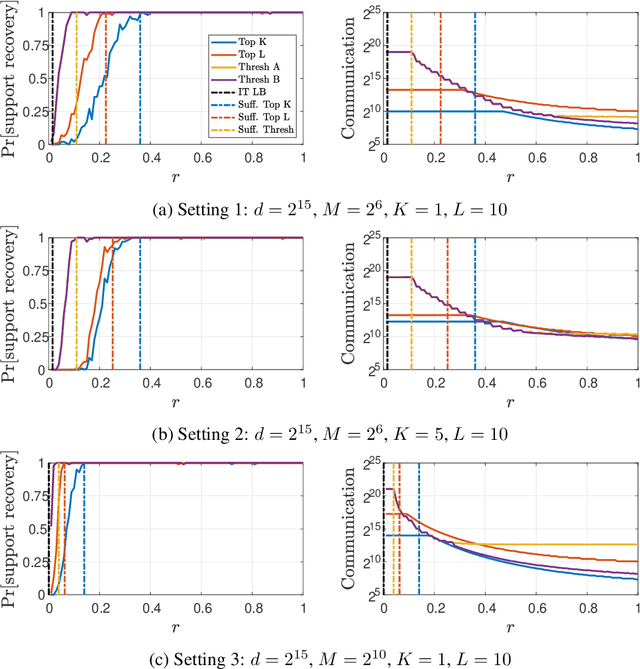
We consider the problem of sparse normal means estimation in a distributed setting with communication constraints. We assume there are $M$ machines, each holding a $d$-dimensional observation of a $K$-sparse vector $\mu$ corrupted by additive Gaussian noise. A central fusion machine is connected to the $M$ machines in a star topology, and its goal is to estimate the vector $\mu$ with a low communication budget. Previous works have shown that to achieve the centralized minimax rate for the $\ell_2$ risk, the total communication must be high - at least linear in the dimension $d$. This phenomenon occurs, however, at very weak signals. We show that once the signal-to-noise ratio (SNR) is slightly higher, the support of $\mu$ can be correctly recovered with much less communication. Specifically, we present two algorithms for the distributed sparse normal means problem, and prove that above a certain SNR threshold, with high probability, they recover the correct support with total communication that is sublinear in the dimension $d$. Furthermore, the communication decreases exponentially as a function of signal strength. If in addition $KM\ll d$, then with an additional round of sublinear communication, our algorithms achieve the centralized rate for the $\ell_2$ risk. Finally, we present simulations that illustrate the performance of our algorithms in different parameter regimes.

Improved Convergence Guarantees for Learning Gaussian Mixture Models by EM and Gradient EM

We consider the problem of estimating the parameters a Gaussian Mixture Model with K components of known weights, all with an identity covariance matrix. We make two contributions. First, at the population level, we present a sharper analysis of the local convergence of EM and gradient EM, compared to previous works. Assuming a separation of $\Omega(\sqrt{\log K})$, we prove convergence of both methods to the global optima from an initialization region larger than those of previous works. Specifically, the initial guess of each component can be as far as (almost) half its distance to the nearest Gaussian. This is essentially the largest possible contraction region. Our second contribution are improved sample size requirements for accurate estimation by EM and gradient EM. In previous works, the required number of samples had a quadratic dependence on the maximal separation between the K components, and the resulting error estimate increased linearly with this maximal separation. In this manuscript we show that both quantities depend only logarithmically on the maximal separation.