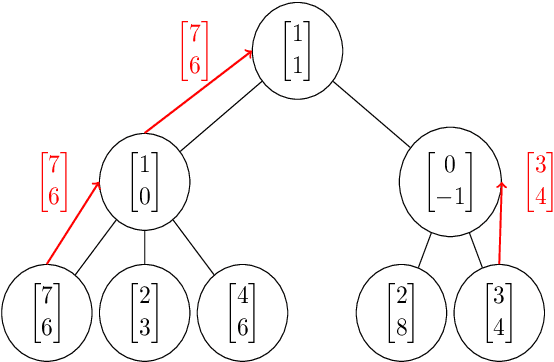
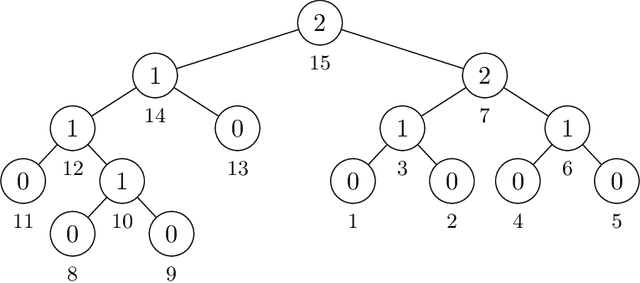
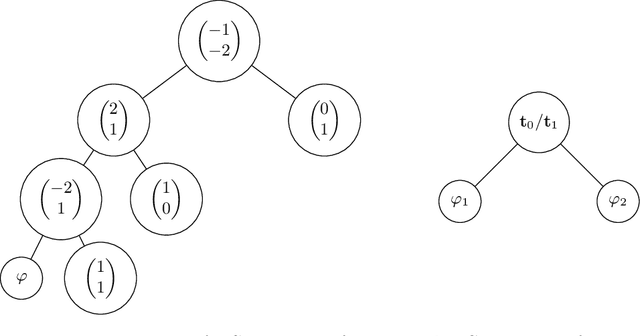
Compositional Reasoning with Transformers, RNNs, and Chain of Thought

We study and compare the expressive power of transformers, RNNs, and transformers with chain of thought tokens on a simple and natural class of problems we term Compositional Reasoning Questions (CRQ). This family captures problems like evaluating Boolean formulas and multi-step word problems. Assuming standard hardness assumptions from circuit complexity and communication complexity, we prove that none of these three architectures is capable of solving CRQs unless some hyperparameter (depth, embedding dimension, and number of chain of thought tokens, respectively) grows with the size of the input. We also provide a construction for each architecture that solves CRQs. For transformers, our construction uses depth that is logarithmic in the problem size. For RNNs, logarithmic embedding dimension is necessary and sufficient, so long as the inputs are provided in a certain order. (Otherwise, a linear dimension is necessary). For transformers with chain of thought, our construction uses $n$ CoT tokens. These results show that, while CRQs are inherently hard, there are several different ways for language models to overcome this hardness. Even for a single class of problems, each architecture has strengths and weaknesses, and none is strictly better than the others.

On the Benefits of Rank in Attention Layers

Attention-based mechanisms are widely used in machine learning, most prominently in transformers. However, hyperparameters such as the rank of the attention matrices and the number of heads are scaled nearly the same way in all realizations of this architecture, without theoretical justification. In this work we show that there are dramatic trade-offs between the rank and number of heads of the attention mechanism. Specifically, we present a simple and natural target function that can be represented using a single full-rank attention head for any context length, but that cannot be approximated by low-rank attention unless the number of heads is exponential in the embedding dimension, even for short context lengths. Moreover, we prove that, for short context lengths, adding depth allows the target to be approximated by low-rank attention. For long contexts, we conjecture that full-rank attention is necessary. Finally, we present experiments with off-the-shelf transformers that validate our theoretical findings.

Spectral Top-Down Recovery of Latent Tree Models

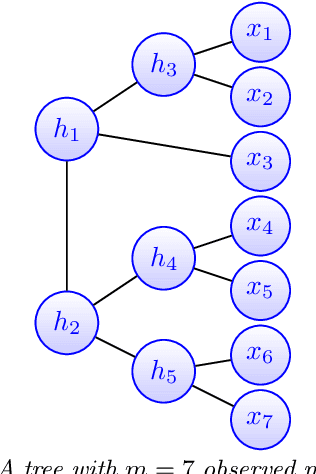
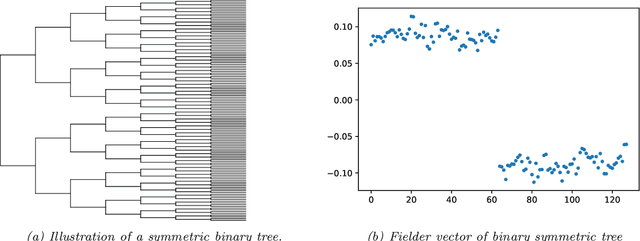
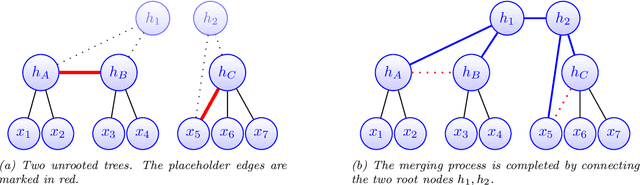
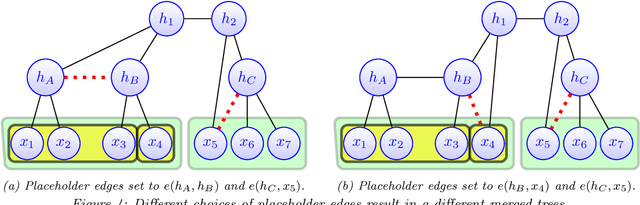
Modeling the distribution of high dimensional data by a latent tree graphical model is a common approach in multiple scientific domains. A common task is to infer the underlying tree structure given only observations of the terminal nodes. Many algorithms for tree recovery are computationally intensive, which limits their applicability to trees of moderate size. For large trees, a common approach, termed divide-and-conquer, is to recover the tree structure in two steps. First, recover the structure separately for multiple randomly selected subsets of the terminal nodes. Second, merge the resulting subtrees to form a full tree. Here, we develop Spectral Top-Down Recovery (STDR), a divide-and-conquer approach for inference of large latent tree models. Unlike previous methods, STDR's partitioning step is non-random. Instead, it is based on the Fiedler vector of a suitable Laplacian matrix related to the observed nodes. We prove that under certain conditions this partitioning is consistent with the tree structure. This, in turn leads to a significantly simpler merging procedure of the small subtrees. We prove that STDR is statistically consistent, and bound the number of samples required to accurately recover the tree with high probability. Using simulated data from several common tree models in phylogenetics, we demonstrate that STDR has a significant advantage in terms of runtime, with improved or similar accuracy.

Spectral neighbor joining for reconstruction of latent tree models

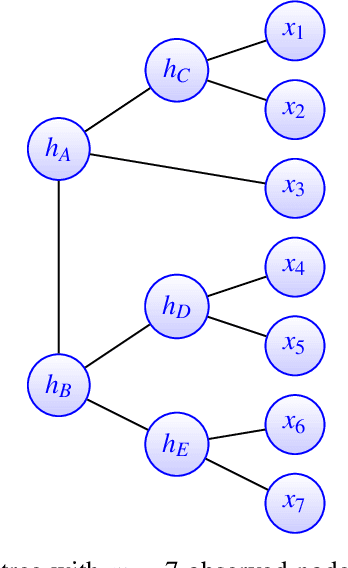
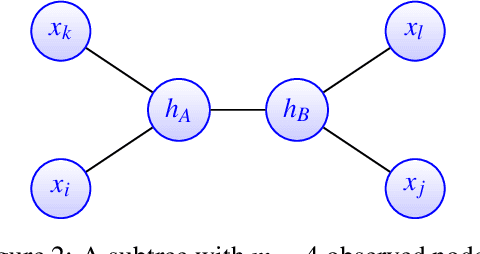
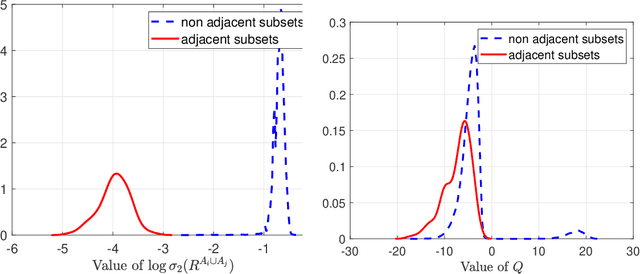
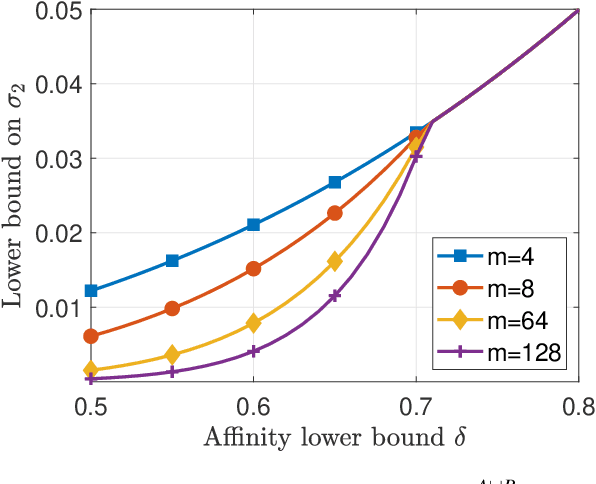
A key assumption in multiple scientific applications is that the distribution of observed data can be modeled by a latent tree graphical model. An important example is phylogenetics, where the tree models the evolutionary lineages of various organisms. Given a set of independent realizations of the random variables at the leaves of the tree, a common task is to infer the underlying tree topology. In this work we develop Spectral Neighbor Joining (SNJ), a novel method to recover latent tree graphical models. In contrast to distance based methods, SNJ is based on a spectral measure of similarity between all pairs of observed variables. We prove that SNJ is consistent, and derive a sufficient condition for correct tree recovery from an estimated similarity matrix. Combining this condition with a concentration of measure result on the similarity matrix, we bound the number of samples required to recover the tree with high probability. We illustrate via extensive simulations that SNJ requires fewer samples to accurately recover trees in regimes where the tree contains a large number of leaves or long edges. We provide theoretical support for this observation by analyzing the model of a perfect binary tree.

Finding Syntactic Representations in Neural Stacks

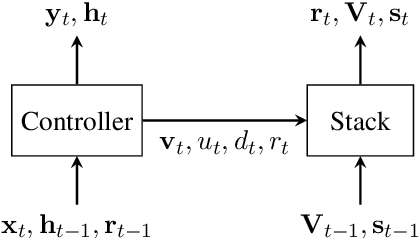
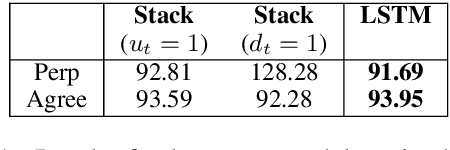
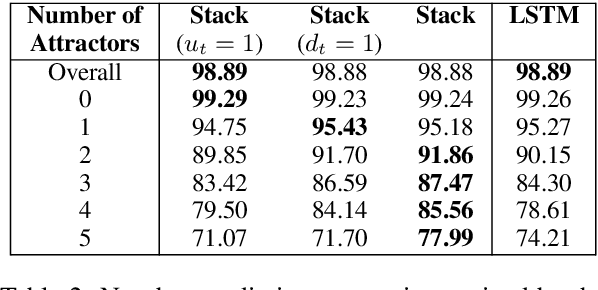
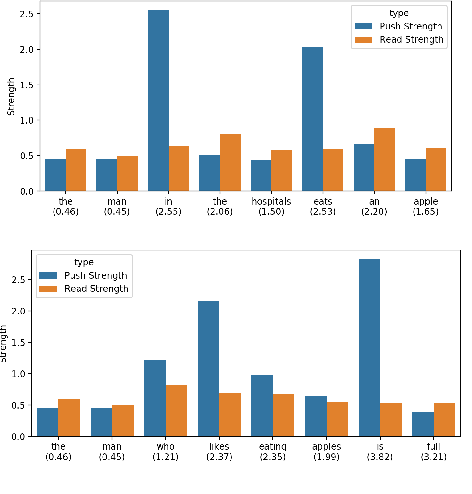
Neural network architectures have been augmented with differentiable stacks in order to introduce a bias toward learning hierarchy-sensitive regularities. It has, however, proven difficult to assess the degree to which such a bias is effective, as the operation of the differentiable stack is not always interpretable. In this paper, we attempt to detect the presence of latent representations of hierarchical structure through an exploration of the unsupervised learning of constituency structure. Using a technique due to Shen et al. (2018a,b), we extract syntactic trees from the pushing behavior of stack RNNs trained on language modeling and classification objectives. We find that our models produce parses that reflect natural language syntactic constituencies, demonstrating that stack RNNs do indeed infer linguistically relevant hierarchical structure.

Context-Free Transductions with Neural Stacks

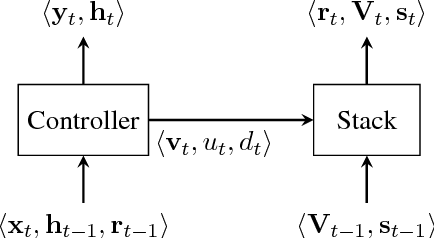
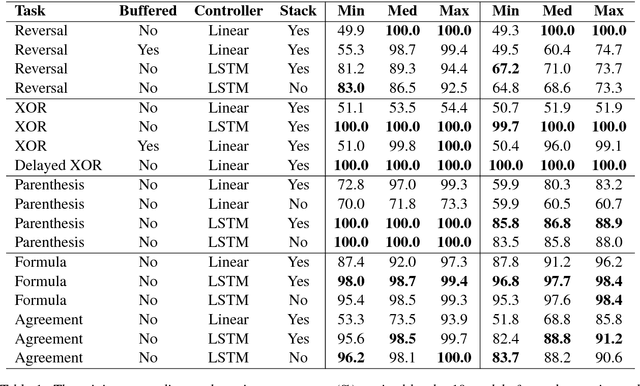
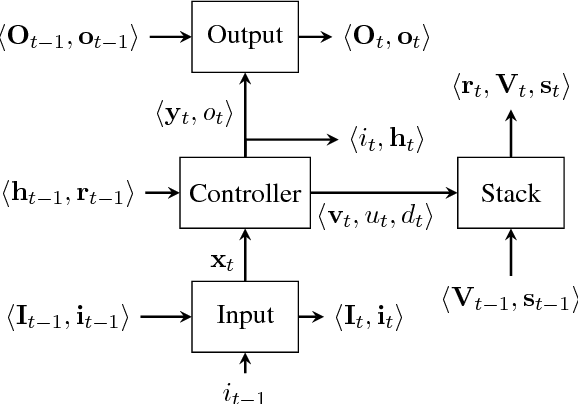
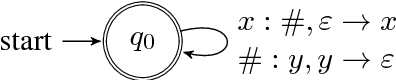
This paper analyzes the behavior of stack-augmented recurrent neural network (RNN) models. Due to the architectural similarity between stack RNNs and pushdown transducers, we train stack RNN models on a number of tasks, including string reversal, context-free language modelling, and cumulative XOR evaluation. Examining the behavior of our networks, we show that stack-augmented RNNs can discover intuitive stack-based strategies for solving our tasks. However, stack RNNs are more difficult to train than classical architectures such as LSTMs. Rather than employ stack-based strategies, more complex networks often find approximate solutions by using the stack as unstructured memory.