Simulating Hard Attention Using Soft Attention

We study conditions under which transformers using soft attention can simulate hard attention, that is, effectively focus all attention on a subset of positions. First, we examine several variants of linear temporal logic, whose formulas have been previously been shown to be computable using hard attention transformers. We demonstrate how soft attention transformers can compute formulas of these logics using unbounded positional embeddings or temperature scaling. Second, we demonstrate how temperature scaling allows softmax transformers to simulate a large subclass of average-hard attention transformers, those that have what we call the uniform-tieless property.

Transformers as Transducers

We study the sequence-to-sequence mapping capacity of transformers by relating them to finite transducers, and find that they can express surprisingly large classes of transductions. We do so using variants of RASP, a programming language designed to help people "think like transformers," as an intermediate representation. We extend the existing Boolean variant B-RASP to sequence-to-sequence functions and show that it computes exactly the first-order rational functions (such as string rotation). Then, we introduce two new extensions. B-RASP[pos] enables calculations on positions (such as copying the first half of a string) and contains all first-order regular functions. S-RASP adds prefix sum, which enables additional arithmetic operations (such as squaring a string) and contains all first-order polyregular functions. Finally, we show that masked average-hard attention transformers can simulate S-RASP. A corollary of our results is a new proof that transformer decoders are Turing-complete.

Transformers as Recognizers of Formal Languages: A Survey on Expressivity

As transformers have gained prominence in natural language processing, some researchers have investigated theoretically what problems they can and cannot solve, by treating problems as formal languages. Exploring questions such as this will help to compare transformers with other models, and transformer variants with one another, for various tasks. Work in this subarea has made considerable progress in recent years. Here, we undertake a comprehensive survey of this work, documenting the diverse assumptions that underlie different results and providing a unified framework for harmonizing seemingly contradictory findings.

Masked Hard-Attention Transformers and Boolean RASP Recognize Exactly the Star-Free Languages

We consider transformer encoders with hard attention (in which all attention is focused on exactly one position) and strict future masking (in which each position only attends to positions strictly to its left), and prove that the class of languages recognized by these networks is exactly the star-free languages. Adding position embeddings increases the class of recognized languages to other well-studied classes. A key technique in these proofs is Boolean RASP, a variant of RASP that is restricted to Boolean values. Via the star-free languages, we relate transformers to first-order logic, temporal logic, and algebraic automata theory.

Formal Language Recognition by Hard Attention Transformers: Perspectives from Circuit Complexity

This paper analyzes three formal models of Transformer encoders that differ in the form of their self-attention mechanism: unique hard attention (UHAT); generalized unique hard attention (GUHAT), which generalizes UHAT; and averaging hard attention (AHAT). We show that UHAT and GUHAT Transformers, viewed as string acceptors, can only recognize formal languages in the complexity class AC$^0$, the class of languages recognizable by families of Boolean circuits of constant depth and polynomial size. This upper bound subsumes Hahn's (2020) results that GUHAT cannot recognize the DYCK languages or the PARITY language, since those languages are outside AC$^0$ (Furst et al., 1984). In contrast, the non-AC$^0$ languages MAJORITY and DYCK-1 are recognizable by AHAT networks, implying that AHAT can recognize languages that UHAT and GUHAT cannot.

Regular omega-Languages with an Informative Right Congruence

A regular language is almost fully characterized by its right congruence relation. Indeed, a regular language can always be recognized by a DFA isomorphic to the automaton corresponding to its right congruence, henceforth the Rightcon automaton. The same does not hold for regular omega-languages. The right congruence of a regular omega-language is not informative enough; many regular omega-languages have a trivial right congruence, and in general it is not always possible to define an omega-automaton recognizing a given language that is isomorphic to the rightcon automaton. The class of weak regular omega-languages does have an informative right congruence. That is, any weak regular omega-language can always be recognized by a deterministic B\"uchi automaton that is isomorphic to the rightcon automaton. Weak regular omega-languages reside in the lower levels of the expressiveness hierarchy of regular omega-languages. Are there more expressive sub-classes of regular omega languages that have an informative right congruence? Can we fully characterize the class of languages with a trivial right congruence? In this paper we try to place some additional pieces of this big puzzle.

Context-Free Transductions with Neural Stacks

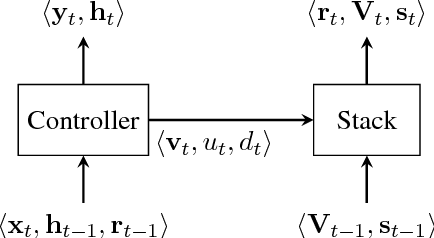
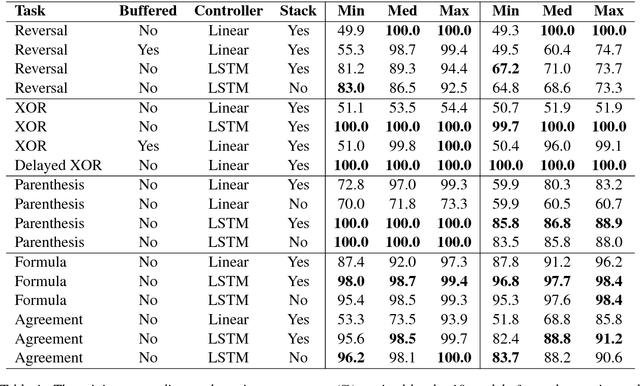
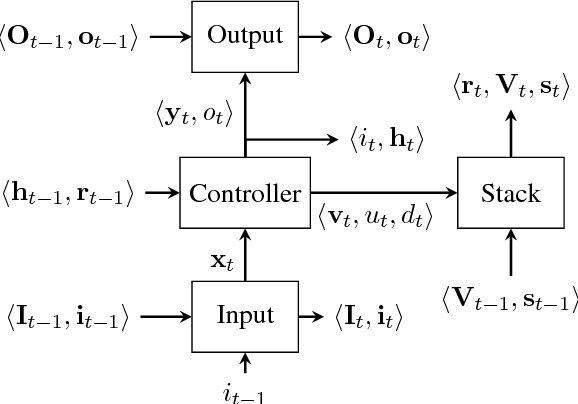
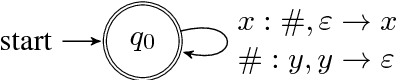
This paper analyzes the behavior of stack-augmented recurrent neural network (RNN) models. Due to the architectural similarity between stack RNNs and pushdown transducers, we train stack RNN models on a number of tasks, including string reversal, context-free language modelling, and cumulative XOR evaluation. Examining the behavior of our networks, we show that stack-augmented RNNs can discover intuitive stack-based strategies for solving our tasks. However, stack RNNs are more difficult to train than classical architectures such as LSTMs. Rather than employ stack-based strategies, more complex networks often find approximate solutions by using the stack as unstructured memory.