Learning shared neural manifolds from multi-subject FMRI data

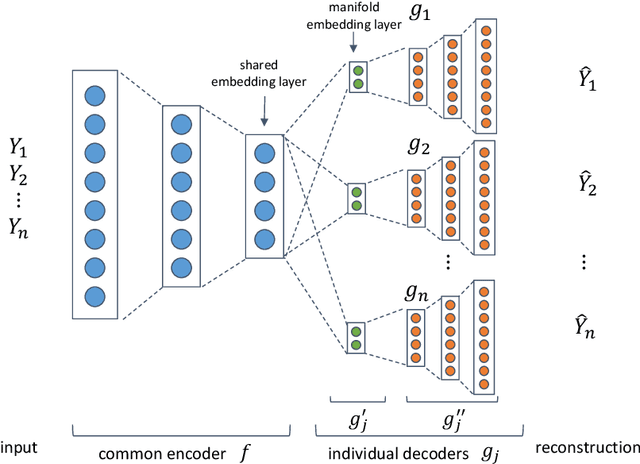
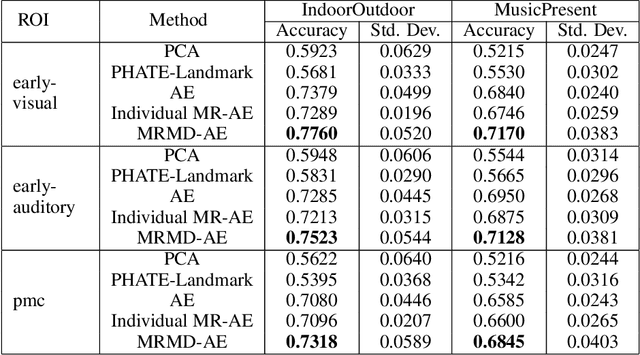
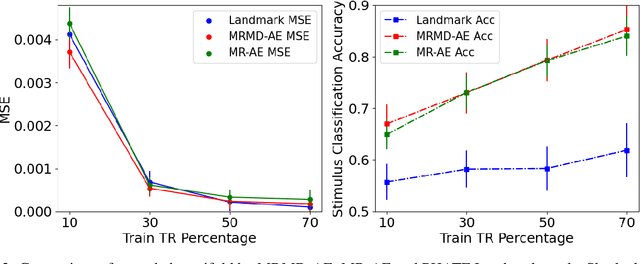
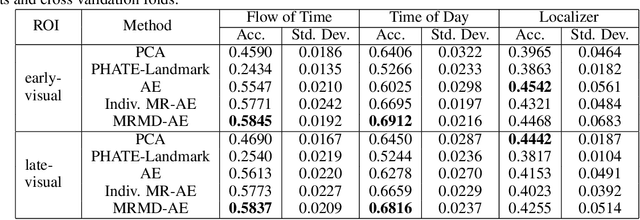
Functional magnetic resonance imaging (fMRI) is a notoriously noisy measurement of brain activity because of the large variations between individuals, signals marred by environmental differences during collection, and spatiotemporal averaging required by the measurement resolution. In addition, the data is extremely high dimensional, with the space of the activity typically having much lower intrinsic dimension. In order to understand the connection between stimuli of interest and brain activity, and analyze differences and commonalities between subjects, it becomes important to learn a meaningful embedding of the data that denoises, and reveals its intrinsic structure. Specifically, we assume that while noise varies significantly between individuals, true responses to stimuli will share common, low-dimensional features between subjects which are jointly discoverable. Similar approaches have been exploited previously but they have mainly used linear methods such as PCA and shared response modeling (SRM). In contrast, we propose a neural network called MRMD-AE (manifold-regularized multiple decoder, autoencoder), that learns a common embedding from multiple subjects in an experiment while retaining the ability to decode to individual raw fMRI signals. We show that our learned common space represents an extensible manifold (where new points not seen during training can be mapped), improves the classification accuracy of stimulus features of unseen timepoints, as well as improves cross-subject translation of fMRI signals. We believe this framework can be used for many downstream applications such as guided brain-computer interface (BCI) training in the future.

Uncovering the Folding Landscape of RNA Secondary Structure with Deep Graph Embeddings

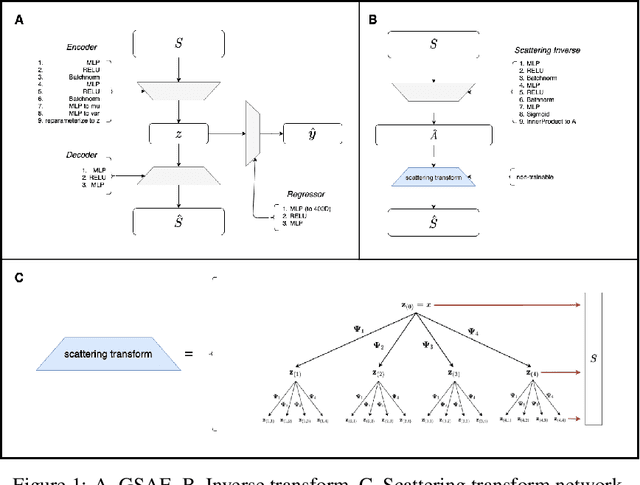
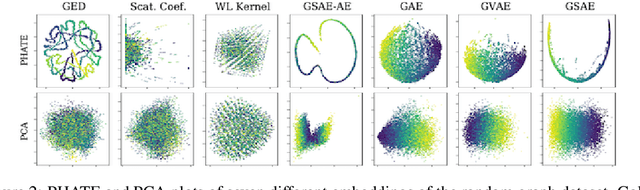
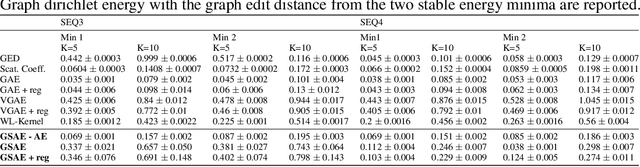
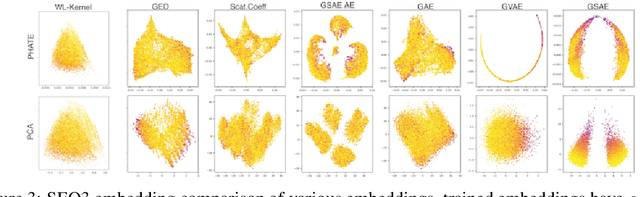
Biomolecular graph analysis has recently gained much attention in the emerging field of geometric deep learning. While numerous approaches aim to train classifiers that accurately predict molecular properties from graphs that encode their structure, an equally important task is to organize biomolecular graphs in ways that expose meaningful relations and variations between them. We propose a geometric scattering autoencoder (GSAE) network for learning such graph embeddings. Our embedding network first extracts rich graph features using the recently proposed geometric scattering transform. Then, it leverages a semi-supervised variational autoencoder to extract a low-dimensional embedding that retains the information in these features that enable prediction of molecular properties as well as characterize graphs. Our approach is based on the intuition that geometric scattering generates multi-resolution features with in-built invariance to deformations, but as they are unsupervised, these features may not be tuned for optimally capturing relevant domain-specific properties. We demonstrate the effectiveness of our approach to data exploration of RNA foldings. Like proteins, RNA molecules can fold to create low energy functional structures such as hairpins, but the landscape of possible folds and fold sequences are not well visualized by existing methods. We show that GSAE organizes RNA graphs both by structure and energy, accurately reflecting bistable RNA structures. Furthermore, it enables interpolation of embedded molecule sequences mimicking folding trajectories. Finally, using an auxiliary inverse-scattering model, we demonstrate our ability to generate synthetic RNA graphs along the trajectory thus providing hypothetical folding sequences for further analysis.

Context-Free Transductions with Neural Stacks

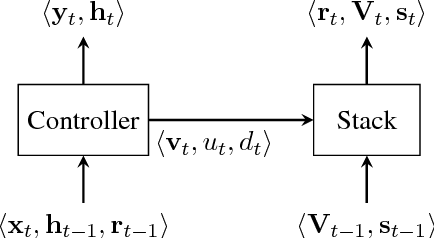
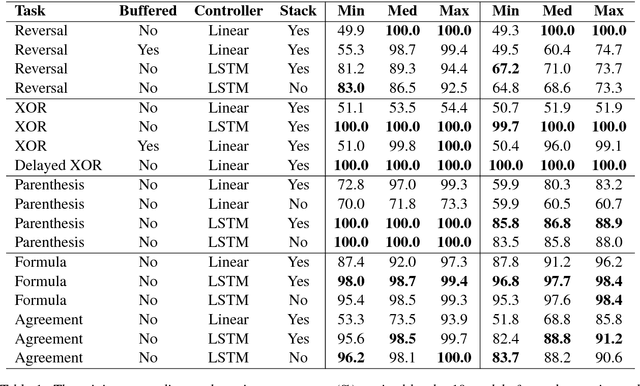
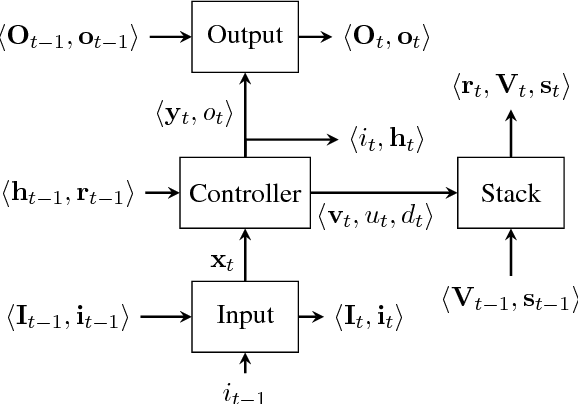
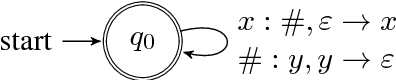
This paper analyzes the behavior of stack-augmented recurrent neural network (RNN) models. Due to the architectural similarity between stack RNNs and pushdown transducers, we train stack RNN models on a number of tasks, including string reversal, context-free language modelling, and cumulative XOR evaluation. Examining the behavior of our networks, we show that stack-augmented RNNs can discover intuitive stack-based strategies for solving our tasks. However, stack RNNs are more difficult to train than classical architectures such as LSTMs. Rather than employ stack-based strategies, more complex networks often find approximate solutions by using the stack as unstructured memory.