Gumbel-Softmax Flow Matching with Straight-Through Guidance for Controllable Biological Sequence Generation

Flow matching in the continuous simplex has emerged as a promising strategy for DNA sequence design, but struggles to scale to higher simplex dimensions required for peptide and protein generation. We introduce Gumbel-Softmax Flow and Score Matching, a generative framework on the simplex based on a novel Gumbel-Softmax interpolant with a time-dependent temperature. Using this interpolant, we introduce Gumbel-Softmax Flow Matching by deriving a parameterized velocity field that transports from smooth categorical distributions to distributions concentrated at a single vertex of the simplex. We alternatively present Gumbel-Softmax Score Matching which learns to regress the gradient of the probability density. Our framework enables high-quality, diverse generation and scales efficiently to higher-dimensional simplices. To enable training-free guidance, we propose Straight-Through Guided Flows (STGFlow), a classifier-based guidance method that leverages straight-through estimators to steer the unconditional velocity field toward optimal vertices of the simplex. STGFlow enables efficient inference-time guidance using classifiers pre-trained on clean sequences, and can be used with any discrete flow method. Together, these components form a robust framework for controllable de novo sequence generation. We demonstrate state-of-the-art performance in conditional DNA promoter design, sequence-only protein generation, and target-binding peptide design for rare disease treatment.

Feynman-Kac Correctors in Diffusion: Annealing, Guidance, and Product of Experts

While score-based generative models are the model of choice across diverse domains, there are limited tools available for controlling inference-time behavior in a principled manner, e.g. for composing multiple pretrained models. Existing classifier-free guidance methods use a simple heuristic to mix conditional and unconditional scores to approximately sample from conditional distributions. However, such methods do not approximate the intermediate distributions, necessitating additional 'corrector' steps. In this work, we provide an efficient and principled method for sampling from a sequence of annealed, geometric-averaged, or product distributions derived from pretrained score-based models. We derive a weighted simulation scheme which we call Feynman-Kac Correctors (FKCs) based on the celebrated Feynman-Kac formula by carefully accounting for terms in the appropriate partial differential equations (PDEs). To simulate these PDEs, we propose Sequential Monte Carlo (SMC) resampling algorithms that leverage inference-time scaling to improve sampling quality. We empirically demonstrate the utility of our methods by proposing amortized sampling via inference-time temperature annealing, improving multi-objective molecule generation using pretrained models, and improving classifier-free guidance for text-to-image generation. Our code is available at https://github.com/martaskrt/fkc-diffusion.

Scalable Equilibrium Sampling with Sequential Boltzmann Generators

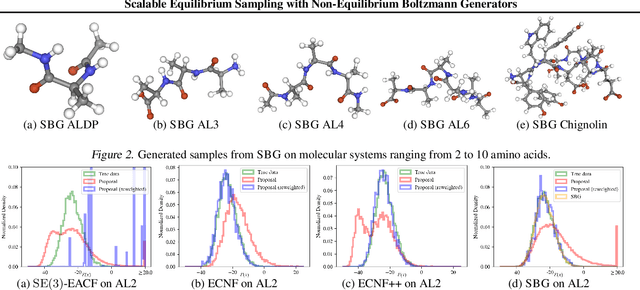
Scalable sampling of molecular states in thermodynamic equilibrium is a long-standing challenge in statistical physics. Boltzmann generators tackle this problem by pairing powerful normalizing flows with importance sampling to obtain statistically independent samples under the target distribution. In this paper, we extend the Boltzmann generator framework and introduce Sequential Boltzmann generators (SBG) with two key improvements. The first is a highly efficient non-equivariant Transformer-based normalizing flow operating directly on all-atom Cartesian coordinates. In contrast to equivariant continuous flows of prior methods, we leverage exactly invertible non-equivariant architectures which are highly efficient both during sample generation and likelihood computation. As a result, this unlocks more sophisticated inference strategies beyond standard importance sampling. More precisely, as a second key improvement we perform inference-time scaling of flow samples using annealed Langevin dynamics which transports samples toward the target distribution leading to lower variance (annealed) importance weights which enable higher fidelity resampling with sequential Monte Carlo. SBG achieves state-of-the-art performance w.r.t. all metrics on molecular systems, demonstrating the first equilibrium sampling in Cartesian coordinates of tri, tetra, and hexapeptides that were so far intractable for prior Boltzmann generators.

Path Planning for Masked Diffusion Model Sampling

In this paper, we investigate how the order in which tokens are unmasked during masked diffusion models (MDMs) inference affects generative quality. We derive an expanded evidence lower bound (ELBO) that introduces a planner, responsible for selecting which tokens to unmask at each step. Our analysis suggests that alternative unmasking strategies can improve generative performance. Based on these insights, we propose Path Planning (P2), a sampling framework that leverages pre-trained BERT or the denoiser itself to guide unmasking decisions. P2 generalizes all known MDM sampling strategies and enables significant improvements across diverse domains including language generation (in-context learning, code generation, story infilling, mathematical reasoning, reverse curse correction) and biological sequence generation (protein and RNA sequences).

The Superposition of Diffusion Models Using the Itô Density Estimator

The Cambrian explosion of easily accessible pre-trained diffusion models suggests a demand for methods that combine multiple different pre-trained diffusion models without incurring the significant computational burden of re-training a larger combined model. In this paper, we cast the problem of combining multiple pre-trained diffusion models at the generation stage under a novel proposed framework termed superposition. Theoretically, we derive superposition from rigorous first principles stemming from the celebrated continuity equation and design two novel algorithms tailor-made for combining diffusion models in SuperDiff. SuperDiff leverages a new scalable It\^o density estimator for the log likelihood of the diffusion SDE which incurs no additional overhead compared to the well-known Hutchinson's estimator needed for divergence calculations. We demonstrate that SuperDiff is scalable to large pre-trained diffusion models as superposition is performed solely through composition during inference, and also enjoys painless implementation as it combines different pre-trained vector fields through an automated re-weighting scheme. Notably, we show that SuperDiff is efficient during inference time, and mimics traditional composition operators such as the logical OR and the logical AND. We empirically demonstrate the utility of using SuperDiff for generating more diverse images on CIFAR-10, more faithful prompt conditioned image editing using Stable Diffusion, and improved unconditional de novo structure design of proteins. https://github.com/necludov/super-diffusion

Trajectory Flow Matching with Applications to Clinical Time Series Modeling

Modeling stochastic and irregularly sampled time series is a challenging problem found in a wide range of applications, especially in medicine. Neural stochastic differential equations (Neural SDEs) are an attractive modeling technique for this problem, which parameterize the drift and diffusion terms of an SDE with neural networks. However, current algorithms for training Neural SDEs require backpropagation through the SDE dynamics, greatly limiting their scalability and stability. To address this, we propose Trajectory Flow Matching (TFM), which trains a Neural SDE in a simulation-free manner, bypassing backpropagation through the dynamics. TFM leverages the flow matching technique from generative modeling to model time series. In this work we first establish necessary conditions for TFM to learn time series data. Next, we present a reparameterization trick which improves training stability. Finally, we adapt TFM to the clinical time series setting, demonstrating improved performance on three clinical time series datasets both in terms of absolute performance and uncertainty prediction.

Steering Masked Discrete Diffusion Models via Discrete Denoising Posterior Prediction

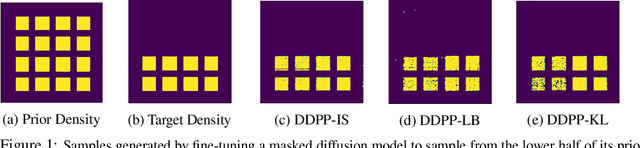
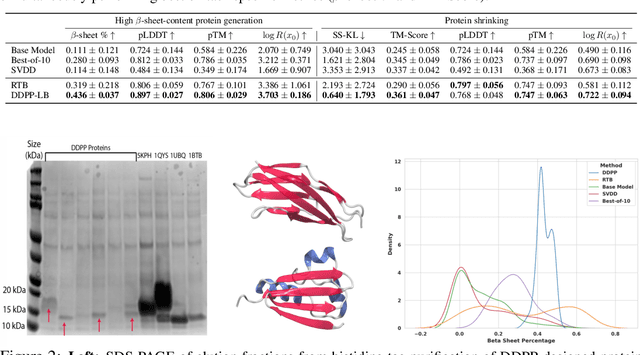
Generative modeling of discrete data underlies important applications spanning text-based agents like ChatGPT to the design of the very building blocks of life in protein sequences. However, application domains need to exert control over the generated data by steering the generative process - typically via RLHF - to satisfy a specified property, reward, or affinity metric. In this paper, we study the problem of steering Masked Diffusion Models (MDMs), a recent class of discrete diffusion models that offer a compelling alternative to traditional autoregressive models. We introduce Discrete Denoising Posterior Prediction (DDPP), a novel framework that casts the task of steering pre-trained MDMs as a problem of probabilistic inference by learning to sample from a target Bayesian posterior. Our DDPP framework leads to a family of three novel objectives that are all simulation-free, and thus scalable while applying to general non-differentiable reward functions. Empirically, we instantiate DDPP by steering MDMs to perform class-conditional pixel-level image modeling, RLHF-based alignment of MDMs using text-based rewards, and finetuning protein language models to generate more diverse secondary structures and shorter proteins. We substantiate our designs via wet-lab validation, where we observe transient expression of reward-optimized protein sequences.

Meta Flow Matching: Integrating Vector Fields on the Wasserstein Manifold

Numerous biological and physical processes can be modeled as systems of interacting entities evolving continuously over time, e.g. the dynamics of communicating cells or physical particles. Learning the dynamics of such systems is essential for predicting the temporal evolution of populations across novel samples and unseen environments. Flow-based models allow for learning these dynamics at the population level - they model the evolution of the entire distribution of samples. However, current flow-based models are limited to a single initial population and a set of predefined conditions which describe different dynamics. We argue that multiple processes in natural sciences have to be represented as vector fields on the Wasserstein manifold of probability densities. That is, the change of the population at any moment in time depends on the population itself due to the interactions between samples. In particular, this is crucial for personalized medicine where the development of diseases and their respective treatment response depends on the microenvironment of cells specific to each patient. We propose Meta Flow Matching (MFM), a practical approach to integrating along these vector fields on the Wasserstein manifold by amortizing the flow model over the initial populations. Namely, we embed the population of samples using a Graph Neural Network (GNN) and use these embeddings to train a Flow Matching model. This gives MFM the ability to generalize over the initial distributions unlike previously proposed methods. We demonstrate the ability of MFM to improve prediction of individual treatment responses on a large scale multi-patient single-cell drug screen dataset.

Generating Multi-Modal and Multi-Attribute Single-Cell Counts with CFGen

Generative modeling of single-cell RNA-seq data has shown invaluable potential in community-driven tasks such as trajectory inference, batch effect removal and gene expression generation. However, most recent deep models generating synthetic single cells from noise operate on pre-processed continuous gene expression approximations, ignoring the inherently discrete and over-dispersed nature of single-cell data, which limits downstream applications and hinders the incorporation of robust noise models. Moreover, crucial aspects of deep-learning-based synthetic single-cell generation remain underexplored, such as controllable multi-modal and multi-label generation and its role in the performance enhancement of downstream tasks. This work presents Cell Flow for Generation (CFGen), a flow-based conditional generative model for multi-modal single-cell counts, which explicitly accounts for the discrete nature of the data. Our results suggest improved recovery of crucial biological data characteristics while accounting for novel generative tasks such as conditioning on multiple attributes and boosting rare cell type classification via data augmentation. By showcasing CFGen on a diverse set of biological datasets and settings, we provide evidence of its value to the fields of computational biology and deep generative models.

ImageFlowNet: Forecasting Multiscale Trajectories of Disease Progression with Irregularly-Sampled Longitudinal Medical Images

The forecasting of disease progression from images is a holy grail for clinical decision making. However, this task is complicated by the inherent high dimensionality, temporal sparsity and sampling irregularity in longitudinal image acquisitions. Existing methods often rely on extracting hand-crafted features and performing time-series analysis in this vector space, leading to a loss of rich spatial information within the images. To overcome these challenges, we introduce ImageFlowNet, a novel framework that learns latent-space flow fields that evolve multiscale representations in joint embedding spaces using neural ODEs and SDEs to model disease progression in the image domain. Notably, ImageFlowNet learns multiscale joint representation spaces by combining cohorts of patients together so that information can be transferred between the patient samples. The dynamics then provide plausible trajectories of progression, with the SDE providing alternative trajectories from the same starting point. We provide theoretical insights that support our formulation of ODEs, and motivate our regularizations involving high-level visual features, latent space organization, and trajectory smoothness. We then demonstrate ImageFlowNet's effectiveness through empirical evaluations on three longitudinal medical image datasets depicting progression in retinal geographic atrophy, multiple sclerosis, and glioblastoma.