Learn to Guide Your Diffusion Model

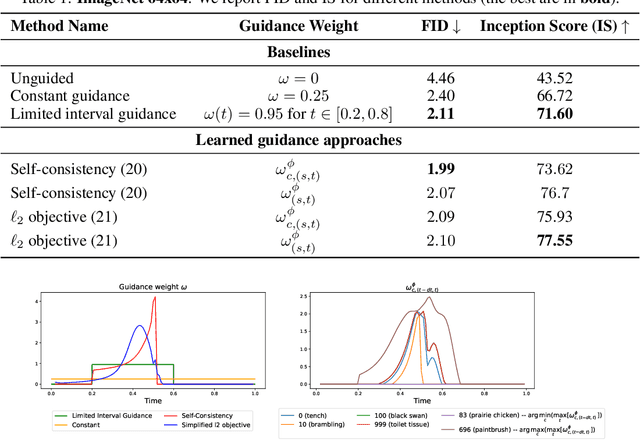
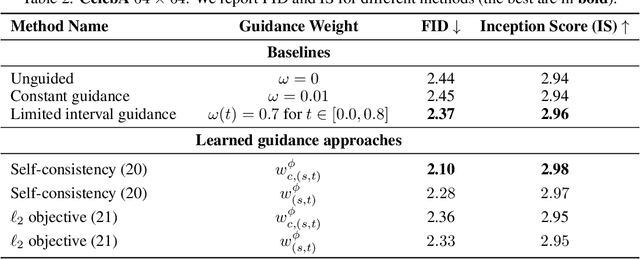
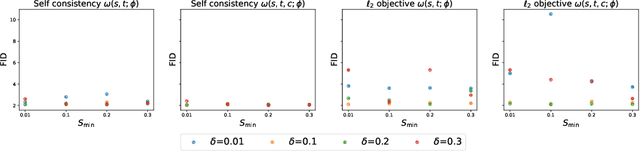
Classifier-free guidance (CFG) is a widely used technique for improving the perceptual quality of samples from conditional diffusion models. It operates by linearly combining conditional and unconditional score estimates using a guidance weight $\omega$. While a large, static weight can markedly improve visual results, this often comes at the cost of poorer distributional alignment. In order to better approximate the target conditional distribution, we instead learn guidance weights $\omega_{c,(s,t)}$, which are continuous functions of the conditioning $c$, the time $t$ from which we denoise, and the time $s$ towards which we denoise. We achieve this by minimizing the distributional mismatch between noised samples from the true conditional distribution and samples from the guided diffusion process. We extend our framework to reward guided sampling, enabling the model to target distributions tilted by a reward function $R(x_0,c)$, defined on clean data and a conditioning $c$. We demonstrate the effectiveness of our methodology on low-dimensional toy examples and high-dimensional image settings, where we observe improvements in Fr\'echet inception distance (FID) for image generation. In text-to-image applications, we observe that employing a reward function given by the CLIP score leads to guidance weights that improve image-prompt alignment.

Source Separation by Flow Matching

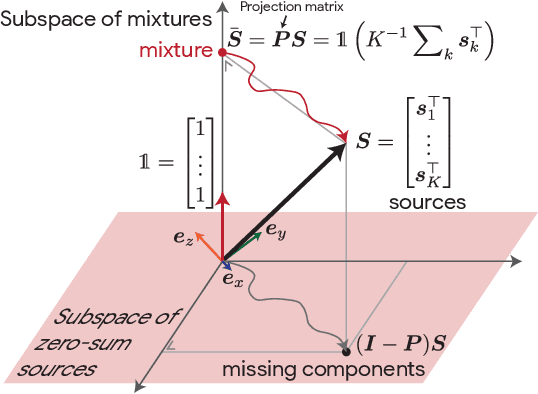
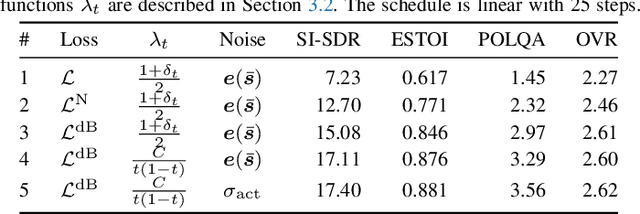
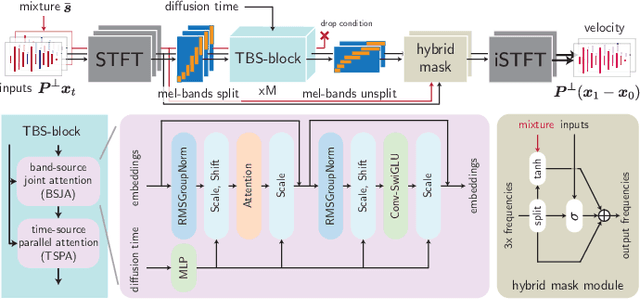
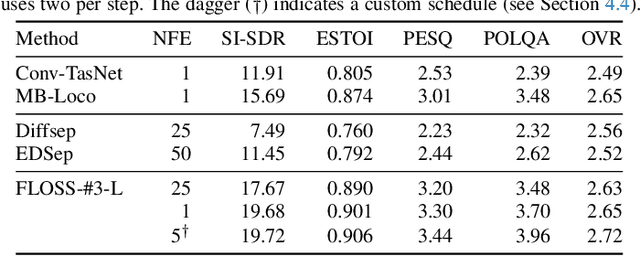
We consider the problem of single-channel audio source separation with the goal of reconstructing $K$ sources from their mixture. We address this ill-posed problem with FLOSS (FLOw matching for Source Separation), a constrained generation method based on flow matching, ensuring strict mixture consistency. Flow matching is a general methodology that, when given samples from two probability distributions defined on the same space, learns an ordinary differential equation to output a sample from one of the distributions when provided with a sample from the other. In our context, we have access to samples from the joint distribution of $K$ sources and so the corresponding samples from the lower-dimensional distribution of their mixture. To apply flow matching, we augment these mixture samples with artificial noise components to ensure the resulting "augmented" distribution matches the dimensionality of the $K$ source distribution. Additionally, as any permutation of the sources yields the same mixture, we adopt an equivariant formulation of flow matching which relies on a suitable custom-designed neural network architecture. We demonstrate the performance of the method for the separation of overlapping speech.

Feynman-Kac Correctors in Diffusion: Annealing, Guidance, and Product of Experts

While score-based generative models are the model of choice across diverse domains, there are limited tools available for controlling inference-time behavior in a principled manner, e.g. for composing multiple pretrained models. Existing classifier-free guidance methods use a simple heuristic to mix conditional and unconditional scores to approximately sample from conditional distributions. However, such methods do not approximate the intermediate distributions, necessitating additional 'corrector' steps. In this work, we provide an efficient and principled method for sampling from a sequence of annealed, geometric-averaged, or product distributions derived from pretrained score-based models. We derive a weighted simulation scheme which we call Feynman-Kac Correctors (FKCs) based on the celebrated Feynman-Kac formula by carefully accounting for terms in the appropriate partial differential equations (PDEs). To simulate these PDEs, we propose Sequential Monte Carlo (SMC) resampling algorithms that leverage inference-time scaling to improve sampling quality. We empirically demonstrate the utility of our methods by proposing amortized sampling via inference-time temperature annealing, improving multi-objective molecule generation using pretrained models, and improving classifier-free guidance for text-to-image generation. Our code is available at https://github.com/martaskrt/fkc-diffusion.

Distributional Diffusion Models with Scoring Rules

Diffusion models generate high-quality synthetic data. They operate by defining a continuous-time forward process which gradually adds Gaussian noise to data until fully corrupted. The corresponding reverse process progressively "denoises" a Gaussian sample into a sample from the data distribution. However, generating high-quality outputs requires many discretization steps to obtain a faithful approximation of the reverse process. This is expensive and has motivated the development of many acceleration methods. We propose to accomplish sample generation by learning the posterior {\em distribution} of clean data samples given their noisy versions, instead of only the mean of this distribution. This allows us to sample from the probability transitions of the reverse process on a coarse time scale, significantly accelerating inference with minimal degradation of the quality of the output. This is accomplished by replacing the standard regression loss used to estimate conditional means with a scoring rule. We validate our method on image and robot trajectory generation, where we consistently outperform standard diffusion models at few discretization steps.

Accelerated Diffusion Models via Speculative Sampling

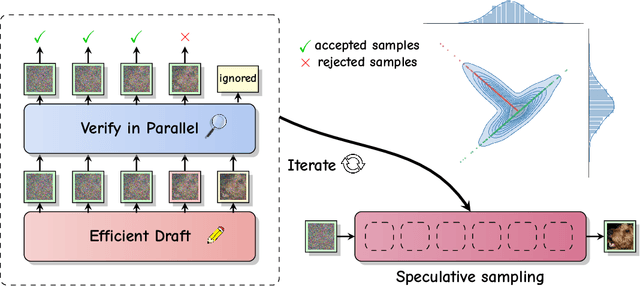
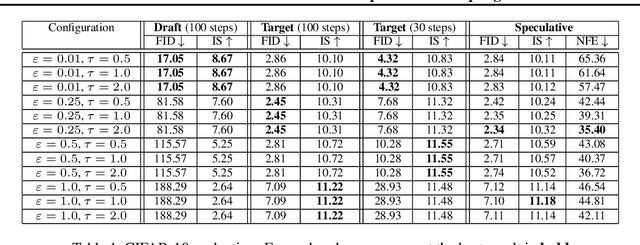
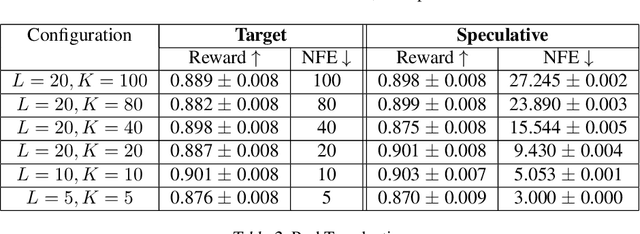
Speculative sampling is a popular technique for accelerating inference in Large Language Models by generating candidate tokens using a fast draft model and accepting or rejecting them based on the target model's distribution. While speculative sampling was previously limited to discrete sequences, we extend it to diffusion models, which generate samples via continuous, vector-valued Markov chains. In this context, the target model is a high-quality but computationally expensive diffusion model. We propose various drafting strategies, including a simple and effective approach that does not require training a draft model and is applicable out of the box to any diffusion model. Our experiments demonstrate significant generation speedup on various diffusion models, halving the number of function evaluations, while generating exact samples from the target model.

Prompting Strategies for Enabling Large Language Models to Infer Causation from Correlation

The reasoning abilities of Large Language Models (LLMs) are attracting increasing attention. In this work, we focus on causal reasoning and address the task of establishing causal relationships based on correlation information, a highly challenging problem on which several LLMs have shown poor performance. We introduce a prompting strategy for this problem that breaks the original task into fixed subquestions, with each subquestion corresponding to one step of a formal causal discovery algorithm, the PC algorithm. The proposed prompting strategy, PC-SubQ, guides the LLM to follow these algorithmic steps, by sequentially prompting it with one subquestion at a time, augmenting the next subquestion's prompt with the answer to the previous one(s). We evaluate our approach on an existing causal benchmark, Corr2Cause: our experiments indicate a performance improvement across five LLMs when comparing PC-SubQ to baseline prompting strategies. Results are robust to causal query perturbations, when modifying the variable names or paraphrasing the expressions.

Score-Optimal Diffusion Schedules

Denoising diffusion models (DDMs) offer a flexible framework for sampling from high dimensional data distributions. DDMs generate a path of probability distributions interpolating between a reference Gaussian distribution and a data distribution by incrementally injecting noise into the data. To numerically simulate the sampling process, a discretisation schedule from the reference back towards clean data must be chosen. An appropriate discretisation schedule is crucial to obtain high quality samples. However, beyond hand crafted heuristics, a general method for choosing this schedule remains elusive. This paper presents a novel algorithm for adaptively selecting an optimal discretisation schedule with respect to a cost that we derive. Our cost measures the work done by the simulation procedure to transport samples from one point in the diffusion path to the next. Our method does not require hyperparameter tuning and adapts to the dynamics and geometry of the diffusion path. Our algorithm only involves the evaluation of the estimated Stein score, making it scalable to existing pre-trained models at inference time and online during training. We find that our learned schedule recovers performant schedules previously only discovered through manual search and obtains competitive FID scores on image datasets.

Conformalized Credal Regions for Classification with Ambiguous Ground Truth

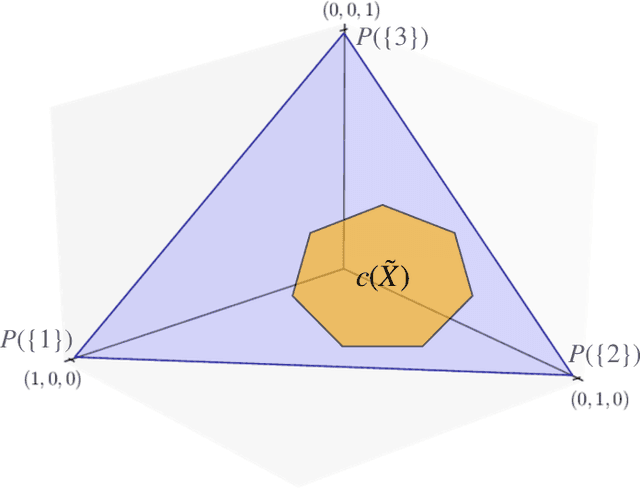
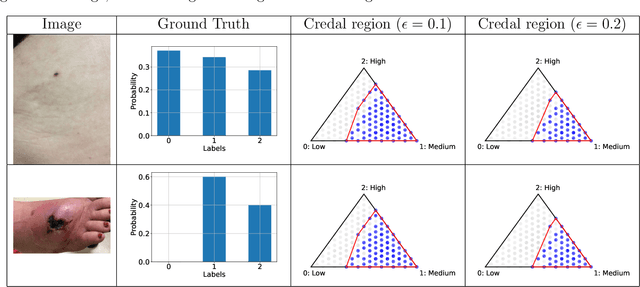
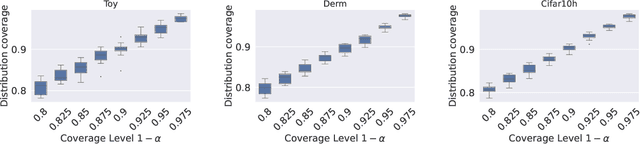
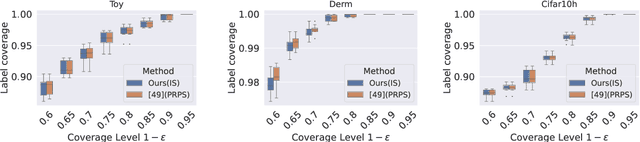
An open question in \emph{Imprecise Probabilistic Machine Learning} is how to empirically derive a credal region (i.e., a closed and convex family of probabilities on the output space) from the available data, without any prior knowledge or assumption. In classification problems, credal regions are a tool that is able to provide provable guarantees under realistic assumptions by characterizing the uncertainty about the distribution of the labels. Building on previous work, we show that credal regions can be directly constructed using conformal methods. This allows us to provide a novel extension of classical conformal prediction to problems with ambiguous ground truth, that is, when the exact labels for given inputs are not exactly known. The resulting construction enjoys desirable practical and theoretical properties: (i) conformal coverage guarantees, (ii) smaller prediction sets (compared to classical conformal prediction regions) and (iii) disentanglement of uncertainty sources (epistemic, aleatoric). We empirically verify our findings on both synthetic and real datasets.

Schrödinger Bridge Flow for Unpaired Data Translation

Mass transport problems arise in many areas of machine learning whereby one wants to compute a map transporting one distribution to another. Generative modeling techniques like Generative Adversarial Networks (GANs) and Denoising Diffusion Models (DDMs) have been successfully adapted to solve such transport problems, resulting in CycleGAN and Bridge Matching respectively. However, these methods do not approximate Optimal Transport (OT) maps, which are known to have desirable properties. Existing techniques approximating OT maps for high-dimensional data-rich problems, such as DDM-based Rectified Flow and Schr\"odinger Bridge procedures, require fully training a DDM-type model at each iteration, or use mini-batch techniques which can introduce significant errors. We propose a novel algorithm to compute the Schr\"odinger Bridge, a dynamic entropy-regularised version of OT, that eliminates the need to train multiple DDM-like models. This algorithm corresponds to a discretisation of a flow of path measures, which we call the Schr\"odinger Bridge Flow, whose only stationary point is the Schr\"odinger Bridge. We demonstrate the performance of our algorithm on a variety of unpaired data translation tasks.

Simplified and Generalized Masked Diffusion for Discrete Data

Masked (or absorbing) diffusion is actively explored as an alternative to autoregressive models for generative modeling of discrete data. However, existing work in this area has been hindered by unnecessarily complex model formulations and unclear relationships between different perspectives, leading to suboptimal parameterization, training objectives, and ad hoc adjustments to counteract these issues. In this work, we aim to provide a simple and general framework that unlocks the full potential of masked diffusion models. We show that the continuous-time variational objective of masked diffusion models is a simple weighted integral of cross-entropy losses. Our framework also enables training generalized masked diffusion models with state-dependent masking schedules. When evaluated by perplexity, our models trained on OpenWebText surpass prior diffusion language models at GPT-2 scale and demonstrate superior performance on 4 out of 5 zero-shot language modeling tasks. Furthermore, our models vastly outperform previous discrete diffusion models on pixel-level image modeling, achieving 2.78~(CIFAR-10) and 3.42 (ImageNet 64$\times$64) bits per dimension that are comparable or better than autoregressive models of similar sizes.