Amortized Sampling with Transferable Normalizing Flows

Efficient equilibrium sampling of molecular conformations remains a core challenge in computational chemistry and statistical inference. Classical approaches such as molecular dynamics or Markov chain Monte Carlo inherently lack amortization; the computational cost of sampling must be paid in-full for each system of interest. The widespread success of generative models has inspired interest into overcoming this limitation through learning sampling algorithms. Despite performing on par with conventional methods when trained on a single system, learned samplers have so far demonstrated limited ability to transfer across systems. We prove that deep learning enables the design of scalable and transferable samplers by introducing Prose, a 280 million parameter all-atom transferable normalizing flow trained on a corpus of peptide molecular dynamics trajectories up to 8 residues in length. Prose draws zero-shot uncorrelated proposal samples for arbitrary peptide systems, achieving the previously intractable transferability across sequence length, whilst retaining the efficient likelihood evaluation of normalizing flows. Through extensive empirical evaluation we demonstrate the efficacy of Prose as a proposal for a variety of sampling algorithms, finding a simple importance sampling-based finetuning procedure to achieve superior performance to established methods such as sequential Monte Carlo on unseen tetrapeptides. We open-source the Prose codebase, model weights, and training dataset, to further stimulate research into amortized sampling methods and finetuning objectives.

Score-Optimal Diffusion Schedules

Denoising diffusion models (DDMs) offer a flexible framework for sampling from high dimensional data distributions. DDMs generate a path of probability distributions interpolating between a reference Gaussian distribution and a data distribution by incrementally injecting noise into the data. To numerically simulate the sampling process, a discretisation schedule from the reference back towards clean data must be chosen. An appropriate discretisation schedule is crucial to obtain high quality samples. However, beyond hand crafted heuristics, a general method for choosing this schedule remains elusive. This paper presents a novel algorithm for adaptively selecting an optimal discretisation schedule with respect to a cost that we derive. Our cost measures the work done by the simulation procedure to transport samples from one point in the diffusion path to the next. Our method does not require hyperparameter tuning and adapts to the dynamics and geometry of the diffusion path. Our algorithm only involves the evaluation of the estimated Stein score, making it scalable to existing pre-trained models at inference time and online during training. We find that our learned schedule recovers performant schedules previously only discovered through manual search and obtains competitive FID scores on image datasets.

A Unified Framework for U-Net Design and Analysis

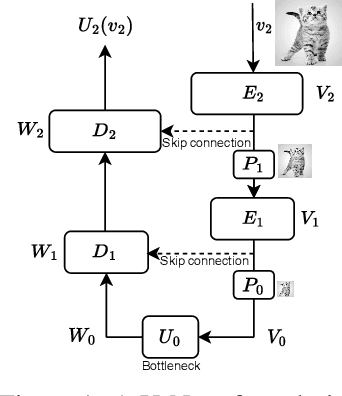
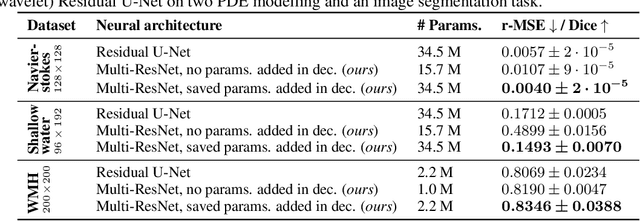
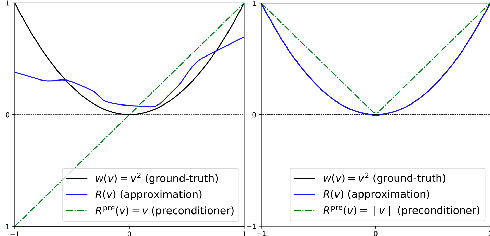
U-Nets are a go-to, state-of-the-art neural architecture across numerous tasks for continuous signals on a square such as images and Partial Differential Equations (PDE), however their design and architecture is understudied. In this paper, we provide a framework for designing and analysing general U-Net architectures. We present theoretical results which characterise the role of the encoder and decoder in a U-Net, their high-resolution scaling limits and their conjugacy to ResNets via preconditioning. We propose Multi-ResNets, U-Nets with a simplified, wavelet-based encoder without learnable parameters. Further, we show how to design novel U-Net architectures which encode function constraints, natural bases, or the geometry of the data. In diffusion models, our framework enables us to identify that high-frequency information is dominated by noise exponentially faster, and show how U-Nets with average pooling exploit this. In our experiments, we demonstrate how Multi-ResNets achieve competitive and often superior performance compared to classical U-Nets in image segmentation, PDE surrogate modelling, and generative modelling with diffusion models. Our U-Net framework paves the way to study the theoretical properties of U-Nets and design natural, scalable neural architectures for a multitude of problems beyond the square.