LENS: LLM-Enabled Narrative Synthesis for Mental Health by Aligning Multimodal Sensing with Language Models

Multimodal health sensing offers rich behavioral signals for assessing mental health, yet translating these numerical time-series measurements into natural language remains challenging. Current LLMs cannot natively ingest long-duration sensor streams, and paired sensor-text datasets are scarce. To address these challenges, we introduce LENS, a framework that aligns multimodal sensing data with language models to generate clinically grounded mental-health narratives. LENS first constructs a large-scale dataset by transforming Ecological Momentary Assessment (EMA) responses related to depression and anxiety symptoms into natural-language descriptions, yielding over 100,000 sensor-text QA pairs from 258 participants. To enable native time-series integration, we train a patch-level encoder that projects raw sensor signals directly into an LLM's representation space. Our results show that LENS outperforms strong baselines on standard NLP metrics and task-specific measures of symptom-severity accuracy. A user study with 13 mental-health professionals further indicates that LENS-produced narratives are comprehensive and clinically meaningful. Ultimately, our approach advances LLMs as interfaces for health sensing, providing a scalable path toward models that can reason over raw behavioral signals and support downstream clinical decision-making.

MotionTeller: Multi-modal Integration of Wearable Time-Series with LLMs for Health and Behavioral Understanding

As wearable sensing becomes increasingly pervasive, a key challenge remains: how can we generate natural language summaries from raw physiological signals such as actigraphy - minute-level movement data collected via accelerometers? In this work, we introduce MotionTeller, a generative framework that natively integrates minute-level wearable activity data with large language models (LLMs). MotionTeller combines a pretrained actigraphy encoder with a lightweight projection module that maps behavioral embeddings into the token space of a frozen decoder-only LLM, enabling free-text, autoregressive generation of daily behavioral summaries. We construct a novel dataset of 54383 (actigraphy, text) pairs derived from real-world NHANES recordings, and train the model using cross-entropy loss with supervision only on the language tokens. MotionTeller achieves high semantic fidelity (BERTScore-F1 = 0.924) and lexical accuracy (ROUGE-1 = 0.722), outperforming prompt-based baselines by 7 percent in ROUGE-1. The average training loss converges to 0.38 by epoch 15, indicating stable optimization. Qualitative analysis confirms that MotionTeller captures circadian structure and behavioral transitions, while PCA plots reveal enhanced cluster alignment in embedding space post-training. Together, these results position MotionTeller as a scalable, interpretable system for transforming wearable sensor data into fluent, human-centered descriptions, introducing new pathways for behavioral monitoring, clinical review, and personalized health interventions.

Decentralized Differentially Private Power Method

We propose a novel Decentralized Differentially Private Power Method (D-DP-PM) for performing Principal Component Analysis (PCA) in networked multi-agent settings. Unlike conventional decentralized PCA approaches where each agent accesses the full n-dimensional sample space, we address the challenging scenario where each agent observes only a subset of dimensions through row-wise data partitioning. Our method ensures $(\epsilon,\delta)$-Differential Privacy (DP) while enabling collaborative estimation of global eigenvectors across the network without requiring a central aggregator. We achieve this by having agents share only local embeddings of the current eigenvector iterate, leveraging both the inherent privacy from random initialization and carefully calibrated Gaussian noise additions. We prove that our algorithm satisfies the prescribed $(\epsilon,\delta)$-DP guarantee and establish convergence rates that explicitly characterize the impact of the network topology. Our theoretical analysis, based on linear dynamics and high-dimensional probability theory, provides tight bounds on both privacy and utility. Experiments on real-world datasets demonstrate that D-DP-PM achieves superior privacy-utility tradeoffs compared to naive local DP approaches, with particularly strong performance in moderate privacy regimes ($\epsilon\in[2, 5]$). The method converges rapidly, allowing practitioners to trade iterations for enhanced privacy while maintaining competitive utility.

A Self-Supervised Framework for Space Object Behaviour Characterisation

Foundation Models, pre-trained on large unlabelled datasets before task-specific fine-tuning, are increasingly being applied to specialised domains. Recent examples include ClimaX for climate and Clay for satellite Earth observation, but a Foundation Model for Space Object Behavioural Analysis has not yet been developed. As orbital populations grow, automated methods for characterising space object behaviour are crucial for space safety. We present a Space Safety and Sustainability Foundation Model focusing on space object behavioural analysis using light curves (LCs). We implemented a Perceiver-Variational Autoencoder (VAE) architecture, pre-trained with self-supervised reconstruction and masked reconstruction on 227,000 LCs from the MMT-9 observatory. The VAE enables anomaly detection, motion prediction, and LC generation. We fine-tuned the model for anomaly detection & motion prediction using two independent LC simulators (CASSANDRA and GRIAL respectively), using CAD models of boxwing, Sentinel-3, SMOS, and Starlink platforms. Our pre-trained model achieved a reconstruction error of 0.01%, identifying potentially anomalous light curves through reconstruction difficulty. After fine-tuning, the model scored 88% and 82% accuracy, with 0.90 and 0.95 ROC AUC scores respectively in both anomaly detection and motion mode prediction (sun-pointing, spin, etc.). Analysis of high-confidence anomaly predictions on real data revealed distinct patterns including characteristic object profiles and satellite glinting. Here, we demonstrate how self-supervised learning can simultaneously enable anomaly detection, motion prediction, and synthetic data generation from rich representations learned in pre-training. Our work therefore supports space safety and sustainability through automated monitoring and simulation capabilities.

Beyond Prompting: Time2Lang -- Bridging Time-Series Foundation Models and Large Language Models for Health Sensing

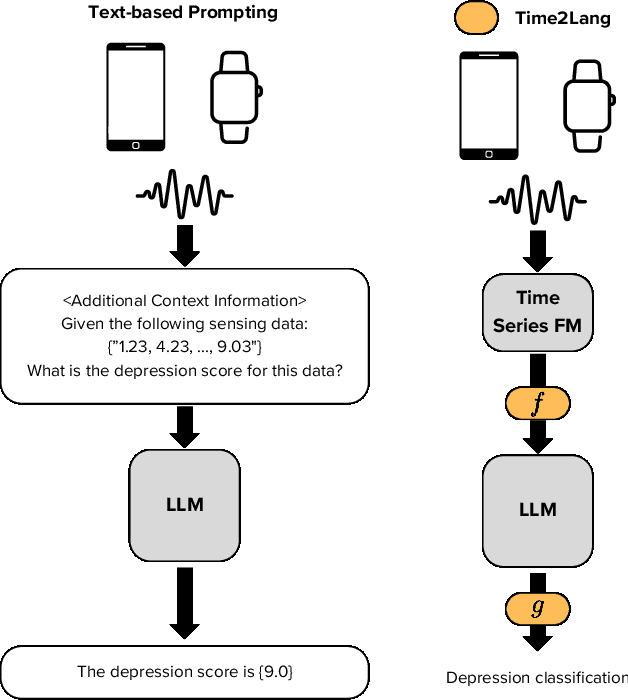
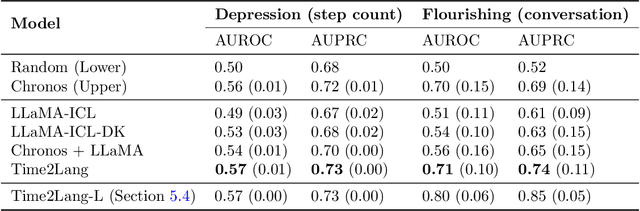
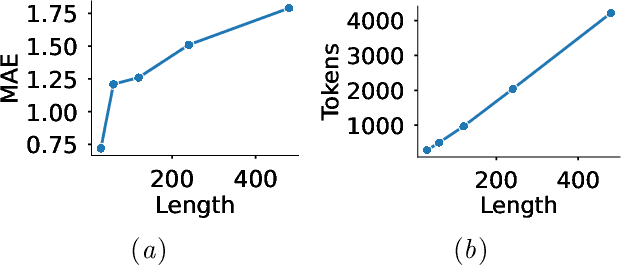
Large language models (LLMs) show promise for health applications when combined with behavioral sensing data. Traditional approaches convert sensor data into text prompts, but this process is prone to errors, computationally expensive, and requires domain expertise. These challenges are particularly acute when processing extended time series data. While time series foundation models (TFMs) have recently emerged as powerful tools for learning representations from temporal data, bridging TFMs and LLMs remains challenging. Here, we present Time2Lang, a framework that directly maps TFM outputs to LLM representations without intermediate text conversion. Our approach first trains on synthetic data using periodicity prediction as a pretext task, followed by evaluation on mental health classification tasks. We validate Time2Lang on two longitudinal wearable and mobile sensing datasets: daily depression prediction using step count data (17,251 days from 256 participants) and flourishing classification based on conversation duration (46 participants over 10 weeks). Time2Lang maintains near constant inference times regardless of input length, unlike traditional prompting methods. The generated embeddings preserve essential time-series characteristics such as auto-correlation. Our results demonstrate that TFMs and LLMs can be effectively integrated while minimizing information loss and enabling performance transfer across these distinct modeling paradigms. To our knowledge, we are the first to integrate a TFM and an LLM for health, thus establishing a foundation for future research combining general-purpose large models for complex healthcare tasks.

Score-Optimal Diffusion Schedules

Denoising diffusion models (DDMs) offer a flexible framework for sampling from high dimensional data distributions. DDMs generate a path of probability distributions interpolating between a reference Gaussian distribution and a data distribution by incrementally injecting noise into the data. To numerically simulate the sampling process, a discretisation schedule from the reference back towards clean data must be chosen. An appropriate discretisation schedule is crucial to obtain high quality samples. However, beyond hand crafted heuristics, a general method for choosing this schedule remains elusive. This paper presents a novel algorithm for adaptively selecting an optimal discretisation schedule with respect to a cost that we derive. Our cost measures the work done by the simulation procedure to transport samples from one point in the diffusion path to the next. Our method does not require hyperparameter tuning and adapts to the dynamics and geometry of the diffusion path. Our algorithm only involves the evaluation of the estimated Stein score, making it scalable to existing pre-trained models at inference time and online during training. We find that our learned schedule recovers performant schedules previously only discovered through manual search and obtains competitive FID scores on image datasets.

Think While You Generate: Discrete Diffusion with Planned Denoising

Discrete diffusion has achieved state-of-the-art performance, outperforming or approaching autoregressive models on standard benchmarks. In this work, we introduce Discrete Diffusion with Planned Denoising (DDPD), a novel framework that separates the generation process into two models: a planner and a denoiser. At inference time, the planner selects which positions to denoise next by identifying the most corrupted positions in need of denoising, including both initially corrupted and those requiring additional refinement. This plan-and-denoise approach enables more efficient reconstruction during generation by iteratively identifying and denoising corruptions in the optimal order. DDPD outperforms traditional denoiser-only mask diffusion methods, achieving superior results on language modeling benchmarks such as text8, OpenWebText, and token-based generation on ImageNet $256 \times 256$. Notably, in language modeling, DDPD significantly reduces the performance gap between diffusion-based and autoregressive methods in terms of generative perplexity. Code is available at https://github.com/liusulin/DDPD.

Generative Flows on Discrete State-Spaces: Enabling Multimodal Flows with Applications to Protein Co-Design

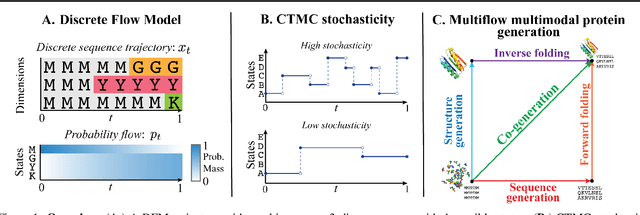
Combining discrete and continuous data is an important capability for generative models. We present Discrete Flow Models (DFMs), a new flow-based model of discrete data that provides the missing link in enabling flow-based generative models to be applied to multimodal continuous and discrete data problems. Our key insight is that the discrete equivalent of continuous space flow matching can be realized using Continuous Time Markov Chains. DFMs benefit from a simple derivation that includes discrete diffusion models as a specific instance while allowing improved performance over existing diffusion-based approaches. We utilize our DFMs method to build a multimodal flow-based modeling framework. We apply this capability to the task of protein co-design, wherein we learn a model for jointly generating protein structure and sequence. Our approach achieves state-of-the-art co-design performance while allowing the same multimodal model to be used for flexible generation of the sequence or structure.

Improved motif-scaffolding with SE(3) flow matching

Protein design often begins with knowledge of a desired function from a motif which motif-scaffolding aims to construct a functional protein around. Recently, generative models have achieved breakthrough success in designing scaffolds for a diverse range of motifs. However, the generated scaffolds tend to lack structural diversity, which can hinder success in wet-lab validation. In this work, we extend FrameFlow, an SE(3) flow matching model for protein backbone generation, to perform motif-scaffolding with two complementary approaches. The first is motif amortization, in which FrameFlow is trained with the motif as input using a data augmentation strategy. The second is motif guidance, which performs scaffolding using an estimate of the conditional score from FrameFlow, and requires no additional training. Both approaches achieve an equivalent or higher success rate than previous state-of-the-art methods, with 2.5 times more structurally diverse scaffolds. Code: https://github.com/ microsoft/frame-flow.

MALCOM-PSGD: Inexact Proximal Stochastic Gradient Descent for Communication-Efficient Decentralized Machine Learning

Recent research indicates that frequent model communication stands as a major bottleneck to the efficiency of decentralized machine learning (ML), particularly for large-scale and over-parameterized neural networks (NNs). In this paper, we introduce MALCOM-PSGD, a new decentralized ML algorithm that strategically integrates gradient compression techniques with model sparsification. MALCOM-PSGD leverages proximal stochastic gradient descent to handle the non-smoothness resulting from the $\ell_1$ regularization in model sparsification. Furthermore, we adapt vector source coding and dithering-based quantization for compressed gradient communication of sparsified models. Our analysis shows that decentralized proximal stochastic gradient descent with compressed communication has a convergence rate of $\mathcal{O}\left(\ln(t)/\sqrt{t}\right)$ assuming a diminishing learning rate and where $t$ denotes the number of iterations. Numerical results verify our theoretical findings and demonstrate that our method reduces communication costs by approximately $75\%$ when compared to the state-of-the-art method.