Denoising Diffusion Probabilistic Models in Six Simple Steps

Denoising Diffusion Probabilistic Models (DDPMs) are a very popular class of deep generative model that have been successfully applied to a diverse range of problems including image and video generation, protein and material synthesis, weather forecasting, and neural surrogates of partial differential equations. Despite their ubiquity it is hard to find an introduction to DDPMs which is simple, comprehensive, clean and clear. The compact explanations necessary in research papers are not able to elucidate all of the different design steps taken to formulate the DDPM and the rationale of the steps that are presented is often omitted to save space. Moreover, the expositions are typically presented from the variational lower bound perspective which is unnecessary and arguably harmful as it obfuscates why the method is working and suggests generalisations that do not perform well in practice. On the other hand, perspectives that take the continuous time-limit are beautiful and general, but they have a high barrier-to-entry as they require background knowledge of stochastic differential equations and probability flow. In this note, we distill down the formulation of the DDPM into six simple steps each of which comes with a clear rationale. We assume that the reader is familiar with fundamental topics in machine learning including basic probabilistic modelling, Gaussian distributions, maximum likelihood estimation, and deep learning.

Improved motif-scaffolding with SE(3) flow matching

Protein design often begins with knowledge of a desired function from a motif which motif-scaffolding aims to construct a functional protein around. Recently, generative models have achieved breakthrough success in designing scaffolds for a diverse range of motifs. However, the generated scaffolds tend to lack structural diversity, which can hinder success in wet-lab validation. In this work, we extend FrameFlow, an SE(3) flow matching model for protein backbone generation, to perform motif-scaffolding with two complementary approaches. The first is motif amortization, in which FrameFlow is trained with the motif as input using a data augmentation strategy. The second is motif guidance, which performs scaffolding using an estimate of the conditional score from FrameFlow, and requires no additional training. Both approaches achieve an equivalent or higher success rate than previous state-of-the-art methods, with 2.5 times more structurally diverse scaffolds. Code: https://github.com/ microsoft/frame-flow.

Autoregressive Conditional Neural Processes

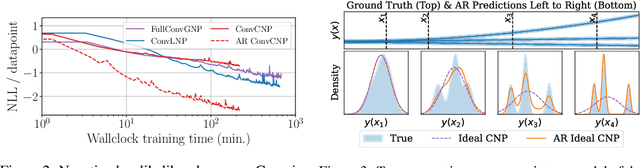
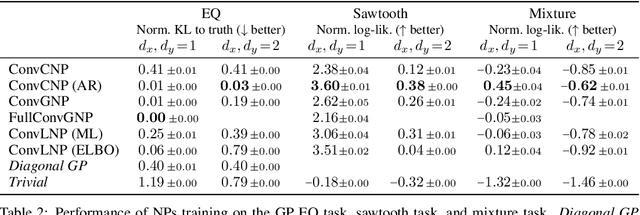
Conditional neural processes (CNPs; Garnelo et al., 2018a) are attractive meta-learning models which produce well-calibrated predictions and are trainable via a simple maximum likelihood procedure. Although CNPs have many advantages, they are unable to model dependencies in their predictions. Various works propose solutions to this, but these come at the cost of either requiring approximate inference or being limited to Gaussian predictions. In this work, we instead propose to change how CNPs are deployed at test time, without any modifications to the model or training procedure. Instead of making predictions independently for every target point, we autoregressively define a joint predictive distribution using the chain rule of probability, taking inspiration from the neural autoregressive density estimator (NADE) literature. We show that this simple procedure allows factorised Gaussian CNPs to model highly dependent, non-Gaussian predictive distributions. Perhaps surprisingly, in an extensive range of tasks with synthetic and real data, we show that CNPs in autoregressive (AR) mode not only significantly outperform non-AR CNPs, but are also competitive with more sophisticated models that are significantly more computationally expensive and challenging to train. This performance is remarkable given that AR CNPs are not trained to model joint dependencies. Our work provides an example of how ideas from neural distribution estimation can benefit neural processes, and motivates research into the AR deployment of other neural process models.

Timewarp: Transferable Acceleration of Molecular Dynamics by Learning Time-Coarsened Dynamics

Molecular dynamics (MD) simulation is a widely used technique to simulate molecular systems, most commonly at the all-atom resolution where the equations of motion are integrated with timesteps on the order of femtoseconds ($1\textrm{fs}=10^{-15}\textrm{s}$). MD is often used to compute equilibrium properties, which requires sampling from an equilibrium distribution such as the Boltzmann distribution. However, many important processes, such as binding and folding, occur over timescales of milliseconds or beyond, and cannot be efficiently sampled with conventional MD. Furthermore, new MD simulations need to be performed from scratch for each molecular system studied. We present Timewarp, an enhanced sampling method which uses a normalising flow as a proposal distribution in a Markov chain Monte Carlo method targeting the Boltzmann distribution. The flow is trained offline on MD trajectories and learns to make large steps in time, simulating the molecular dynamics of $10^{5} - 10^{6}\:\textrm{fs}$. Crucially, Timewarp is transferable between molecular systems: once trained, we show that it generalises to unseen small peptides (2-4 amino acids), exploring their metastable states and providing wall-clock acceleration when sampling compared to standard MD. Our method constitutes an important step towards developing general, transferable algorithms for accelerating MD.

A Note on the Chernoff Bound for Random Variables in the Unit Interval

The Chernoff bound is a well-known tool for obtaining a high probability bound on the expectation of a Bernoulli random variable in terms of its sample average. This bound is commonly used in statistical learning theory to upper bound the generalisation risk of a hypothesis in terms of its empirical risk on held-out data, for the case of a binary-valued loss function. However, the extension of this bound to the case of random variables taking values in the unit interval is less well known in the community. In this note we provide a proof of this extension for convenience and future reference.

How Tight Can PAC-Bayes be in the Small Data Regime?

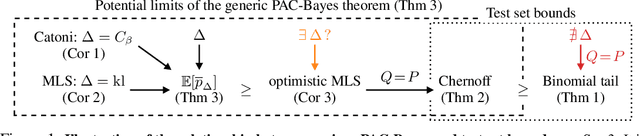
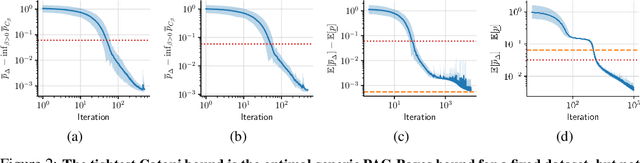
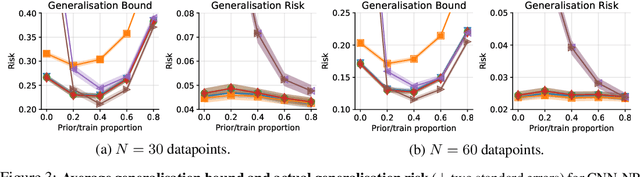
In this paper, we investigate the question: Given a small number of datapoints, for example N = 30, how tight can PAC-Bayes and test set bounds be made? For such small datasets, test set bounds adversely affect generalisation performance by discarding data. In this setting, PAC-Bayes bounds are especially attractive, due to their ability to use all the data to simultaneously learn a posterior and bound its generalisation risk. We focus on the case of i.i.d. data with a bounded loss and consider the generic PAC-Bayes theorem of Germain et al. (2009) and Begin et al. (2016). While their theorem is known to recover many existing PAC-Bayes bounds, it is unclear what the tightest bound derivable from their framework is. Surprisingly, we show that for a fixed learning algorithm and dataset, the tightest bound of this form coincides with the tightest bound of the more restrictive family of bounds considered in Catoni (2007). In contrast, in the more natural case of distributions over datasets, we give examples (both analytic and numerical) showing that the family of bounds in Catoni (2007) can be suboptimal. Within the proof framework of Germain et al. (2009) and Begin et al. (2016), we establish a lower bound on the best bound achievable in expectation, which recovers the Chernoff test set bound in the case when the posterior is equal to the prior. Finally, to illustrate how tight these bounds can potentially be, we study a synthetic one-dimensional classification task in which it is feasible to meta-learn both the prior and the form of the bound to obtain the tightest PAC-Bayes and test set bounds possible. We find that in this simple, controlled scenario, PAC-Bayes bounds are surprisingly competitive with comparable, commonly used Chernoff test set bounds. However, the sharpest test set bounds still lead to better guarantees on the generalisation error than the PAC-Bayes bounds we consider.

The Gaussian Neural Process

Neural Processes (NPs; Garnelo et al., 2018a,b) are a rich class of models for meta-learning that map data sets directly to predictive stochastic processes. We provide a rigorous analysis of the standard maximum-likelihood objective used to train conditional NPs. Moreover, we propose a new member to the Neural Process family called the Gaussian Neural Process (GNP), which models predictive correlations, incorporates translation equivariance, provides universal approximation guarantees, and demonstrates encouraging performance.

Meta-Learning Stationary Stochastic Process Prediction with Convolutional Neural Processes

Stationary stochastic processes (SPs) are a key component of many probabilistic models, such as those for off-the-grid spatio-temporal data. They enable the statistical symmetry of underlying physical phenomena to be leveraged, thereby aiding generalization. Prediction in such models can be viewed as a translation equivariant map from observed data sets to predictive SPs, emphasizing the intimate relationship between stationarity and equivariance. Building on this, we propose the Convolutional Neural Process (ConvNP), which endows Neural Processes (NPs) with translation equivariance and extends convolutional conditional NPs to allow for dependencies in the predictive distribution. The latter enables ConvNPs to be deployed in settings which require coherent samples, such as Thompson sampling or conditional image completion. Moreover, we propose a new maximum-likelihood objective to replace the standard ELBO objective in NPs, which conceptually simplifies the framework and empirically improves performance. We demonstrate the strong performance and generalization capabilities of ConvNPs on 1D regression, image completion, and various tasks with real-world spatio-temporal data.

Convolutional Conditional Neural Processes

We introduce the Convolutional Conditional Neural Process (ConvCNP), a new member of the Neural Process family that models translation equivariance in the data. Translation equivariance is an important inductive bias for many learning problems including time series modelling, spatial data, and images. The model embeds data sets into an infinite-dimensional function space as opposed to a finite-dimensional vector space. To formalize this notion, we extend the theory of neural representations of sets to include functional representations, and demonstrate that any translation-equivariant embedding can be represented using a convolutional deep set. We evaluate ConvCNPs in several settings, demonstrating that they achieve state-of-the-art performance compared to existing NPs. We demonstrate that building in translation equivariance enables zero-shot generalization to challenging, out-of-domain tasks.

Pathologies of Factorised Gaussian and MC Dropout Posteriors in Bayesian Neural Networks

Neural networks provide state-of-the-art performance on a variety of tasks. However, they are often overconfident when making predictions. This inability to properly account for uncertainty limits their application to high-risk decision making, active learning and Bayesian optimisation. To address this, Bayesian inference has been proposed as a framework for improving uncertainty estimates. In practice, Bayesian neural networks rely on poorly understood approximations for computational tractability. We prove that two commonly used approximation methods, the factorised Gaussian assumption and Monte Carlo dropout, lead to pathological estimates of the predictive uncertainty in single hidden layer ReLU networks. This indicates that more flexible approximations are needed to obtain reliable uncertainty estimates.