Scalable Equilibrium Sampling with Sequential Boltzmann Generators

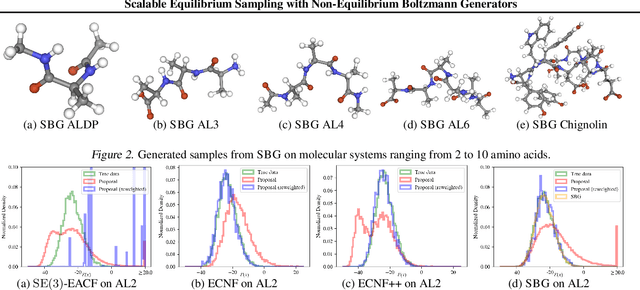
Scalable sampling of molecular states in thermodynamic equilibrium is a long-standing challenge in statistical physics. Boltzmann generators tackle this problem by pairing powerful normalizing flows with importance sampling to obtain statistically independent samples under the target distribution. In this paper, we extend the Boltzmann generator framework and introduce Sequential Boltzmann generators (SBG) with two key improvements. The first is a highly efficient non-equivariant Transformer-based normalizing flow operating directly on all-atom Cartesian coordinates. In contrast to equivariant continuous flows of prior methods, we leverage exactly invertible non-equivariant architectures which are highly efficient both during sample generation and likelihood computation. As a result, this unlocks more sophisticated inference strategies beyond standard importance sampling. More precisely, as a second key improvement we perform inference-time scaling of flow samples using annealed Langevin dynamics which transports samples toward the target distribution leading to lower variance (annealed) importance weights which enable higher fidelity resampling with sequential Monte Carlo. SBG achieves state-of-the-art performance w.r.t. all metrics on molecular systems, demonstrating the first equilibrium sampling in Cartesian coordinates of tri, tetra, and hexapeptides that were so far intractable for prior Boltzmann generators.

Transferable Boltzmann Generators

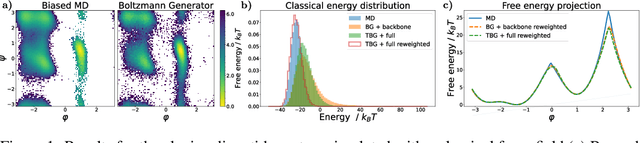
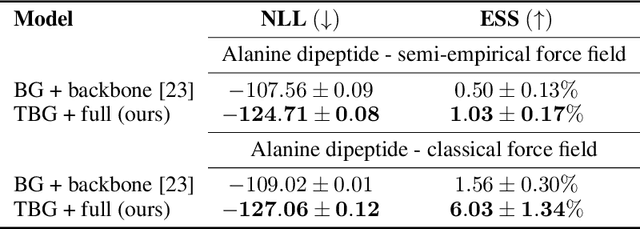
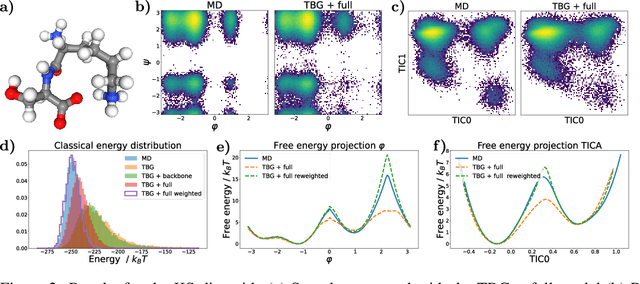
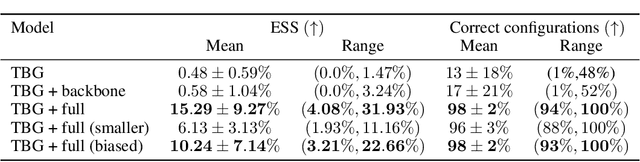
The generation of equilibrium samples of molecular systems has been a long-standing problem in statistical physics. Boltzmann Generators are a generative machine learning method that addresses this issue by learning a transformation via a normalizing flow from a simple prior distribution to the target Boltzmann distribution of interest. Recently, flow matching has been employed to train Boltzmann Generators for small molecular systems in Cartesian coordinates. We extend this work and propose a first framework for Boltzmann Generators that are transferable across chemical space, such that they predict zero-shot Boltzmann distributions for test molecules without being retrained for these systems. These transferable Boltzmann Generators allow approximate sampling from the target distribution of unseen systems, as well as efficient reweighting to the target Boltzmann distribution. The transferability of the proposed framework is evaluated on dipeptides, where we show that it generalizes efficiently to unseen systems. Furthermore, we demonstrate that our proposed architecture enhances the efficiency of Boltzmann Generators trained on single molecular systems.

Equivariant flow matching

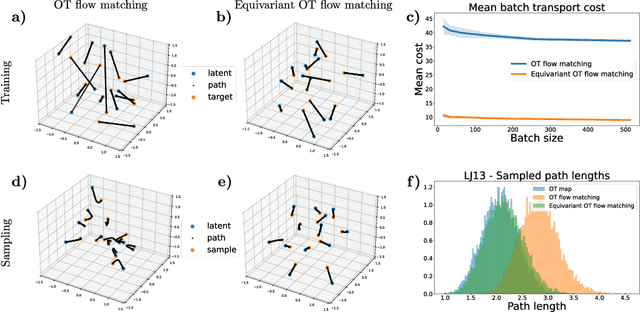
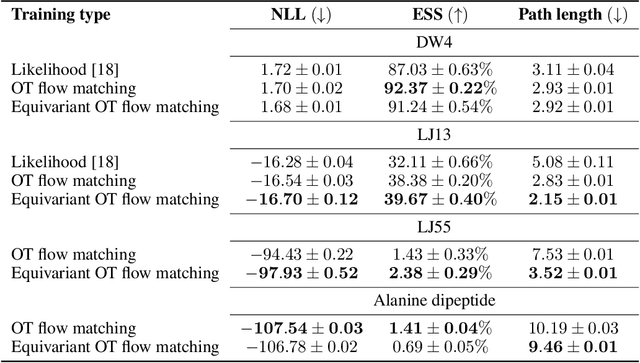
Normalizing flows are a class of deep generative models that are especially interesting for modeling probability distributions in physics, where the exact likelihood of flows allows reweighting to known target energy functions and computing unbiased observables. For instance, Boltzmann generators tackle the long-standing sampling problem in statistical physics by training flows to produce equilibrium samples of many-body systems such as small molecules and proteins. To build effective models for such systems, it is crucial to incorporate the symmetries of the target energy into the model, which can be achieved by equivariant continuous normalizing flows (CNFs). However, CNFs can be computationally expensive to train and generate samples from, which has hampered their scalability and practical application. In this paper, we introduce equivariant flow matching, a new training objective for equivariant CNFs that is based on the recently proposed optimal transport flow matching. Equivariant flow matching exploits the physical symmetries of the target energy for efficient, simulation-free training of equivariant CNFs. We demonstrate the effectiveness of our approach on many-particle systems and a small molecule, alanine dipeptide, where for the first time we obtain a Boltzmann generator with significant sampling efficiency without relying on tailored internal coordinate featurization. Our results show that the equivariant flow matching objective yields flows with shorter integration paths, improved sampling efficiency, and higher scalability compared to existing methods.

Timewarp: Transferable Acceleration of Molecular Dynamics by Learning Time-Coarsened Dynamics

Molecular dynamics (MD) simulation is a widely used technique to simulate molecular systems, most commonly at the all-atom resolution where the equations of motion are integrated with timesteps on the order of femtoseconds ($1\textrm{fs}=10^{-15}\textrm{s}$). MD is often used to compute equilibrium properties, which requires sampling from an equilibrium distribution such as the Boltzmann distribution. However, many important processes, such as binding and folding, occur over timescales of milliseconds or beyond, and cannot be efficiently sampled with conventional MD. Furthermore, new MD simulations need to be performed from scratch for each molecular system studied. We present Timewarp, an enhanced sampling method which uses a normalising flow as a proposal distribution in a Markov chain Monte Carlo method targeting the Boltzmann distribution. The flow is trained offline on MD trajectories and learns to make large steps in time, simulating the molecular dynamics of $10^{5} - 10^{6}\:\textrm{fs}$. Crucially, Timewarp is transferable between molecular systems: once trained, we show that it generalises to unseen small peptides (2-4 amino acids), exploring their metastable states and providing wall-clock acceleration when sampling compared to standard MD. Our method constitutes an important step towards developing general, transferable algorithms for accelerating MD.

Equivariant Flows: exact likelihood generative learning for symmetric densities

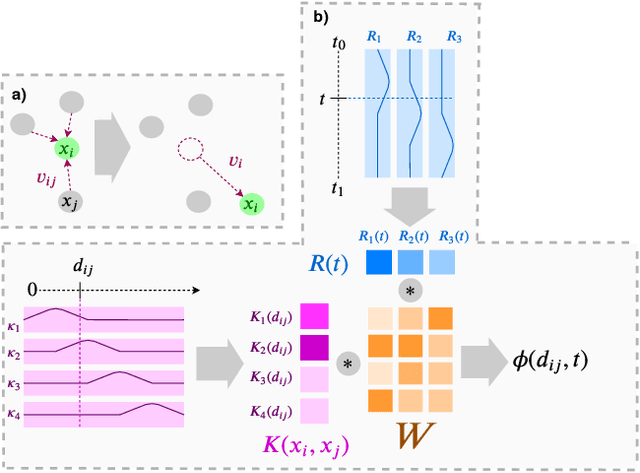
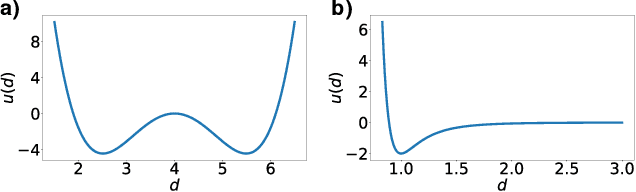
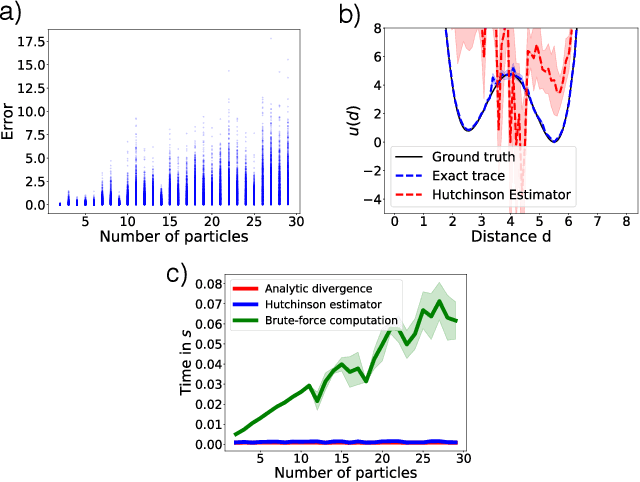
Normalizing flows are exact-likelihood generative neural networks which approximately transform samples from a simple prior distribution to samples of the probability distribution of interest. Recent work showed that such generative models can be utilized in statistical mechanics to sample equilibrium states of many-body systems in physics and chemistry. To scale and generalize these results, it is essential that the natural symmetries in the probability density - in physics defined by the invariances of the target potential - are built into the flow. We provide a theoretical sufficient criterion showing that the distribution generated by equivariant normalizing flows is invariant with respect to these symmetries by design. Furthermore, we propose building blocks for flows which preserve symmetries which are usually found in physical/chemical many-body particle systems. Using benchmark systems motivated from molecular physics, we demonstrate that those symmetry preserving flows can provide better generalization capabilities and sampling efficiency.

Equivariant Flows: sampling configurations for multi-body systems with symmetric energies

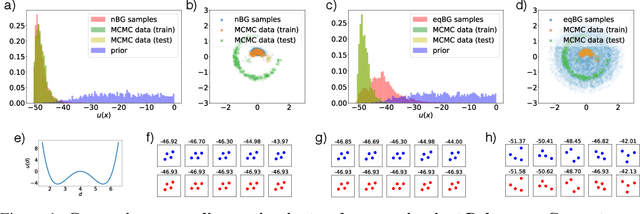
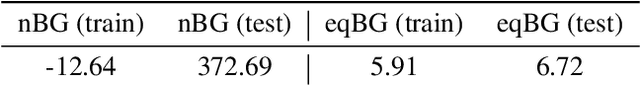
Flows are exact-likelihood generative neural networks that transform samples from a simple prior distribution to the samples of the probability distribution of interest. Boltzmann Generators (BG) combine flows and statistical mechanics to sample equilibrium states of strongly interacting many-body systems such as proteins with 1000 atoms. In order to scale and generalize these results, it is essential that the natural symmetries of the probability density - in physics defined by the invariances of the energy function - are built into the flow. Here we develop theoretical tools for constructing such equivariant flows and demonstrate that a BG that is equivariant with respect to rotations and particle permutations can generalize to sampling nontrivially new configurations where a nonequivariant BG cannot.