Curly Flow Matching for Learning Non-gradient Field Dynamics

Modeling the transport dynamics of natural processes from population-level observations is a ubiquitous problem in the natural sciences. Such models rely on key assumptions about the underlying process in order to enable faithful learning of governing dynamics that mimic the actual system behavior. The de facto assumption in current approaches relies on the principle of least action that results in gradient field dynamics and leads to trajectories minimizing an energy functional between two probability measures. However, many real-world systems, such as cell cycles in single-cell RNA, are known to exhibit non-gradient, periodic behavior, which fundamentally cannot be captured by current state-of-the-art methods such as flow and bridge matching. In this paper, we introduce Curly Flow Matching (Curly-FM), a novel approach that is capable of learning non-gradient field dynamics by designing and solving a Schr\"odinger bridge problem with a non-zero drift reference process -- in stark contrast to typical zero-drift reference processes -- which is constructed using inferred velocities in addition to population snapshot data. We showcase Curly-FM by solving the trajectory inference problems for single cells, computational fluid dynamics, and ocean currents with approximate velocities. We demonstrate that Curly-FM can learn trajectories that better match both the reference process and population marginals. Curly-FM expands flow matching models beyond the modeling of populations and towards the modeling of known periodic behavior in physical systems. Our code repository is accessible at: https://github.com/kpetrovicc/curly-flow-matching.git

Generalised Flow Maps for Few-Step Generative Modelling on Riemannian Manifolds

Geometric data and purpose-built generative models on them have become ubiquitous in high-impact deep learning application domains, ranging from protein backbone generation and computational chemistry to geospatial data. Current geometric generative models remain computationally expensive at inference -- requiring many steps of complex numerical simulation -- as they are derived from dynamical measure transport frameworks such as diffusion and flow-matching on Riemannian manifolds. In this paper, we propose Generalised Flow Maps (GFM), a new class of few-step generative models that generalises the Flow Map framework in Euclidean spaces to arbitrary Riemannian manifolds. We instantiate GFMs with three self-distillation-based training methods: Generalised Lagrangian Flow Maps, Generalised Eulerian Flow Maps, and Generalised Progressive Flow Maps. We theoretically show that GFMs, under specific design decisions, unify and elevate existing Euclidean few-step generative models, such as consistency models, shortcut models, and meanflows, to the Riemannian setting. We benchmark GFMs against other geometric generative models on a suite of geometric datasets, including geospatial data, RNA torsion angles, and hyperbolic manifolds, and achieve state-of-the-art sample quality for single- and few-step evaluations, and superior or competitive log-likelihoods using the implicit probability flow.

RETRO SYNFLOW: Discrete Flow Matching for Accurate and Diverse Single-Step Retrosynthesis

A fundamental problem in organic chemistry is identifying and predicting the series of reactions that synthesize a desired target product molecule. Due to the combinatorial nature of the chemical search space, single-step reactant prediction -- i.e. single-step retrosynthesis -- remains challenging even for existing state-of-the-art template-free generative approaches to produce an accurate yet diverse set of feasible reactions. In this paper, we model single-step retrosynthesis planning and introduce RETRO SYNFLOW (RSF) a discrete flow-matching framework that builds a Markov bridge between the prescribed target product molecule and the reactant molecule. In contrast to past approaches, RSF employs a reaction center identification step to produce intermediate structures known as synthons as a more informative source distribution for the discrete flow. To further enhance diversity and feasibility of generated samples, we employ Feynman-Kac steering with Sequential Monte Carlo based resampling to steer promising generations at inference using a new reward oracle that relies on a forward-synthesis model. Empirically, we demonstrate \nameshort achieves $60.0 \%$ top-1 accuracy, which outperforms the previous SOTA by $20 \%$. We also substantiate the benefits of steering at inference and demonstrate that FK-steering improves top-$5$ round-trip accuracy by $19 \%$ over prior template-free SOTA methods, all while preserving competitive top-$k$ accuracy results.

Scalable Equilibrium Sampling with Sequential Boltzmann Generators

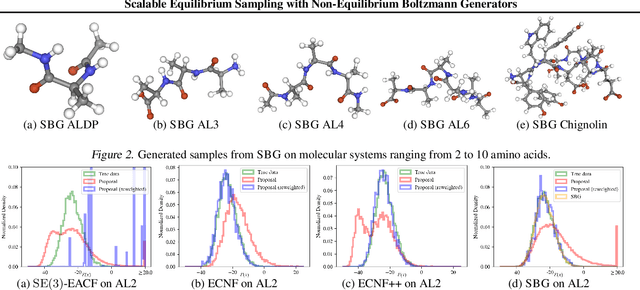
Scalable sampling of molecular states in thermodynamic equilibrium is a long-standing challenge in statistical physics. Boltzmann generators tackle this problem by pairing powerful normalizing flows with importance sampling to obtain statistically independent samples under the target distribution. In this paper, we extend the Boltzmann generator framework and introduce Sequential Boltzmann generators (SBG) with two key improvements. The first is a highly efficient non-equivariant Transformer-based normalizing flow operating directly on all-atom Cartesian coordinates. In contrast to equivariant continuous flows of prior methods, we leverage exactly invertible non-equivariant architectures which are highly efficient both during sample generation and likelihood computation. As a result, this unlocks more sophisticated inference strategies beyond standard importance sampling. More precisely, as a second key improvement we perform inference-time scaling of flow samples using annealed Langevin dynamics which transports samples toward the target distribution leading to lower variance (annealed) importance weights which enable higher fidelity resampling with sequential Monte Carlo. SBG achieves state-of-the-art performance w.r.t. all metrics on molecular systems, demonstrating the first equilibrium sampling in Cartesian coordinates of tri, tetra, and hexapeptides that were so far intractable for prior Boltzmann generators.

The Superposition of Diffusion Models Using the Itô Density Estimator

The Cambrian explosion of easily accessible pre-trained diffusion models suggests a demand for methods that combine multiple different pre-trained diffusion models without incurring the significant computational burden of re-training a larger combined model. In this paper, we cast the problem of combining multiple pre-trained diffusion models at the generation stage under a novel proposed framework termed superposition. Theoretically, we derive superposition from rigorous first principles stemming from the celebrated continuity equation and design two novel algorithms tailor-made for combining diffusion models in SuperDiff. SuperDiff leverages a new scalable It\^o density estimator for the log likelihood of the diffusion SDE which incurs no additional overhead compared to the well-known Hutchinson's estimator needed for divergence calculations. We demonstrate that SuperDiff is scalable to large pre-trained diffusion models as superposition is performed solely through composition during inference, and also enjoys painless implementation as it combines different pre-trained vector fields through an automated re-weighting scheme. Notably, we show that SuperDiff is efficient during inference time, and mimics traditional composition operators such as the logical OR and the logical AND. We empirically demonstrate the utility of using SuperDiff for generating more diverse images on CIFAR-10, more faithful prompt conditioned image editing using Stable Diffusion, and improved unconditional de novo structure design of proteins. https://github.com/necludov/super-diffusion

Steering Masked Discrete Diffusion Models via Discrete Denoising Posterior Prediction

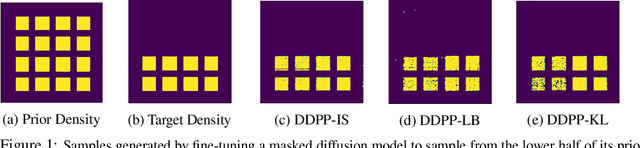
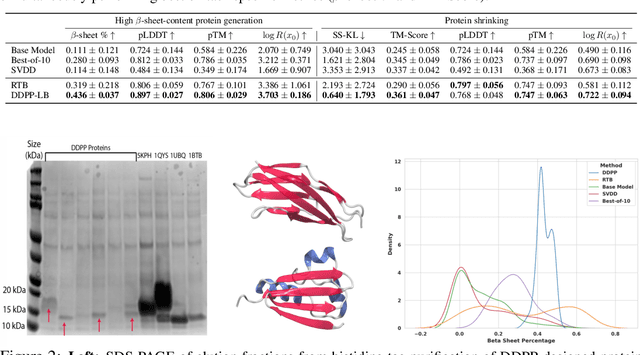
Generative modeling of discrete data underlies important applications spanning text-based agents like ChatGPT to the design of the very building blocks of life in protein sequences. However, application domains need to exert control over the generated data by steering the generative process - typically via RLHF - to satisfy a specified property, reward, or affinity metric. In this paper, we study the problem of steering Masked Diffusion Models (MDMs), a recent class of discrete diffusion models that offer a compelling alternative to traditional autoregressive models. We introduce Discrete Denoising Posterior Prediction (DDPP), a novel framework that casts the task of steering pre-trained MDMs as a problem of probabilistic inference by learning to sample from a target Bayesian posterior. Our DDPP framework leads to a family of three novel objectives that are all simulation-free, and thus scalable while applying to general non-differentiable reward functions. Empirically, we instantiate DDPP by steering MDMs to perform class-conditional pixel-level image modeling, RLHF-based alignment of MDMs using text-based rewards, and finetuning protein language models to generate more diverse secondary structures and shorter proteins. We substantiate our designs via wet-lab validation, where we observe transient expression of reward-optimized protein sequences.

Sequence-Augmented SE(3)-Flow Matching For Conditional Protein Backbone Generation

Proteins are essential for almost all biological processes and derive their diverse functions from complex 3D structures, which are in turn determined by their amino acid sequences. In this paper, we exploit the rich biological inductive bias of amino acid sequences and introduce FoldFlow-2, a novel sequence-conditioned SE(3)-equivariant flow matching model for protein structure generation. FoldFlow-2 presents substantial new architectural features over the previous FoldFlow family of models including a protein large language model to encode sequence, a new multi-modal fusion trunk that combines structure and sequence representations, and a geometric transformer based decoder. To increase diversity and novelty of generated samples -- crucial for de-novo drug design -- we train FoldFlow-2 at scale on a new dataset that is an order of magnitude larger than PDB datasets of prior works, containing both known proteins in PDB and high-quality synthetic structures achieved through filtering. We further demonstrate the ability to align FoldFlow-2 to arbitrary rewards, e.g. increasing secondary structures diversity, by introducing a Reinforced Finetuning (ReFT) objective. We empirically observe that FoldFlow-2 outperforms previous state-of-the-art protein structure-based generative models, improving over RFDiffusion in terms of unconditional generation across all metrics including designability, diversity, and novelty across all protein lengths, as well as exhibiting generalization on the task of equilibrium conformation sampling. Finally, we demonstrate that a fine-tuned FoldFlow-2 makes progress on challenging conditional design tasks such as designing scaffolds for the VHH nanobody.

Metric Flow Matching for Smooth Interpolations on the Data Manifold

Matching objectives underpin the success of modern generative models and rely on constructing conditional paths that transform a source distribution into a target distribution. Despite being a fundamental building block, conditional paths have been designed principally under the assumption of Euclidean geometry, resulting in straight interpolations. However, this can be particularly restrictive for tasks such as trajectory inference, where straight paths might lie outside the data manifold, thus failing to capture the underlying dynamics giving rise to the observed marginals. In this paper, we propose Metric Flow Matching (MFM), a novel simulation-free framework for conditional flow matching where interpolants are approximate geodesics learned by minimizing the kinetic energy of a data-induced Riemannian metric. This way, the generative model matches vector fields on the data manifold, which corresponds to lower uncertainty and more meaningful interpolations. We prescribe general metrics to instantiate MFM, independent of the task, and test it on a suite of challenging problems including LiDAR navigation, unpaired image translation, and modeling cellular dynamics. We observe that MFM outperforms the Euclidean baselines, particularly achieving SOTA on single-cell trajectory prediction.

Fisher Flow Matching for Generative Modeling over Discrete Data

Generative modeling over discrete data has recently seen numerous success stories, with applications spanning language modeling, biological sequence design, and graph-structured molecular data. The predominant generative modeling paradigm for discrete data is still autoregressive, with more recent alternatives based on diffusion or flow-matching falling short of their impressive performance in continuous data settings, such as image or video generation. In this work, we introduce Fisher-Flow, a novel flow-matching model for discrete data. Fisher-Flow takes a manifestly geometric perspective by considering categorical distributions over discrete data as points residing on a statistical manifold equipped with its natural Riemannian metric: the $\textit{Fisher-Rao metric}$. As a result, we demonstrate discrete data itself can be continuously reparameterised to points on the positive orthant of the $d$-hypersphere $\mathbb{S}^d_+$, which allows us to define flows that map any source distribution to target in a principled manner by transporting mass along (closed-form) geodesics of $\mathbb{S}^d_+$. Furthermore, the learned flows in Fisher-Flow can be further bootstrapped by leveraging Riemannian optimal transport leading to improved training dynamics. We prove that the gradient flow induced by Fisher-Flow is optimal in reducing the forward KL divergence. We evaluate Fisher-Flow on an array of synthetic and diverse real-world benchmarks, including designing DNA Promoter, and DNA Enhancer sequences. Empirically, we find that Fisher-Flow improves over prior diffusion and flow-matching models on these benchmarks.

Iterated Denoising Energy Matching for Sampling from Boltzmann Densities

Efficiently generating statistically independent samples from an unnormalized probability distribution, such as equilibrium samples of many-body systems, is a foundational problem in science. In this paper, we propose Iterated Denoising Energy Matching (iDEM), an iterative algorithm that uses a novel stochastic score matching objective leveraging solely the energy function and its gradient -- and no data samples -- to train a diffusion-based sampler. Specifically, iDEM alternates between (I) sampling regions of high model density from a diffusion-based sampler and (II) using these samples in our stochastic matching objective to further improve the sampler. iDEM is scalable to high dimensions as the inner matching objective, is simulation-free, and requires no MCMC samples. Moreover, by leveraging the fast mode mixing behavior of diffusion, iDEM smooths out the energy landscape enabling efficient exploration and learning of an amortized sampler. We evaluate iDEM on a suite of tasks ranging from standard synthetic energy functions to invariant $n$-body particle systems. We show that the proposed approach achieves state-of-the-art performance on all metrics and trains $2-5\times$ faster, which allows it to be the first method to train using energy on the challenging $55$-particle Lennard-Jones system.