Sequence-Augmented SE(3)-Flow Matching For Conditional Protein Backbone Generation

Proteins are essential for almost all biological processes and derive their diverse functions from complex 3D structures, which are in turn determined by their amino acid sequences. In this paper, we exploit the rich biological inductive bias of amino acid sequences and introduce FoldFlow-2, a novel sequence-conditioned SE(3)-equivariant flow matching model for protein structure generation. FoldFlow-2 presents substantial new architectural features over the previous FoldFlow family of models including a protein large language model to encode sequence, a new multi-modal fusion trunk that combines structure and sequence representations, and a geometric transformer based decoder. To increase diversity and novelty of generated samples -- crucial for de-novo drug design -- we train FoldFlow-2 at scale on a new dataset that is an order of magnitude larger than PDB datasets of prior works, containing both known proteins in PDB and high-quality synthetic structures achieved through filtering. We further demonstrate the ability to align FoldFlow-2 to arbitrary rewards, e.g. increasing secondary structures diversity, by introducing a Reinforced Finetuning (ReFT) objective. We empirically observe that FoldFlow-2 outperforms previous state-of-the-art protein structure-based generative models, improving over RFDiffusion in terms of unconditional generation across all metrics including designability, diversity, and novelty across all protein lengths, as well as exhibiting generalization on the task of equilibrium conformation sampling. Finally, we demonstrate that a fine-tuned FoldFlow-2 makes progress on challenging conditional design tasks such as designing scaffolds for the VHH nanobody.

SE(3)-Stochastic Flow Matching for Protein Backbone Generation

The computational design of novel protein structures has the potential to impact numerous scientific disciplines greatly. Toward this goal, we introduce $\text{FoldFlow}$ a series of novel generative models of increasing modeling power based on the flow-matching paradigm over $3\text{D}$ rigid motions -- i.e. the group $\text{SE(3)}$ -- enabling accurate modeling of protein backbones. We first introduce $\text{FoldFlow-Base}$, a simulation-free approach to learning deterministic continuous-time dynamics and matching invariant target distributions on $\text{SE(3)}$. We next accelerate training by incorporating Riemannian optimal transport to create $\text{FoldFlow-OT}$, leading to the construction of both more simple and stable flows. Finally, we design $\text{FoldFlow-SFM}$ coupling both Riemannian OT and simulation-free training to learn stochastic continuous-time dynamics over $\text{SE(3)}$. Our family of $\text{FoldFlow}$ generative models offer several key advantages over previous approaches to the generative modeling of proteins: they are more stable and faster to train than diffusion-based approaches, and our models enjoy the ability to map any invariant source distribution to any invariant target distribution over $\text{SE(3)}$. Empirically, we validate our FoldFlow models on protein backbone generation of up to $300$ amino acids leading to high-quality designable, diverse, and novel samples.

Generating and Imputing Tabular Data via Diffusion and Flow-based Gradient-Boosted Trees

Tabular data is hard to acquire and is subject to missing values. This paper proposes a novel approach to generate and impute mixed-type (continuous and categorical) tabular data using score-based diffusion and conditional flow matching. Contrary to previous work that relies on neural networks as function approximators, we instead utilize XGBoost, a popular Gradient-Boosted Tree (GBT) method. In addition to being elegant, we empirically show on various datasets that our method i) generates highly realistic synthetic data when the training dataset is either clean or tainted by missing data and ii) generates diverse plausible data imputations. Our method often outperforms deep-learning generation methods and can trained in parallel using CPUs without the need for a GPU. To make it easily accessible, we release our code through a Python library on PyPI and an R package on CRAN.

Simulation-free Schrödinger bridges via score and flow matching

We present simulation-free score and flow matching ([SF]$^2$M), a simulation-free objective for inferring stochastic dynamics given unpaired source and target samples drawn from arbitrary distributions. Our method generalizes both the score-matching loss used in the training of diffusion models and the recently proposed flow matching loss used in the training of continuous normalizing flows. [SF]$^2$M interprets continuous-time stochastic generative modeling as a Schr\"odinger bridge (SB) problem. It relies on static entropy-regularized optimal transport, or a minibatch approximation, to efficiently learn the SB without simulating the learned stochastic process. We find that [SF]$^2$M is more efficient and gives more accurate solutions to the SB problem than simulation-based methods from prior work. Finally, we apply [SF]$^2$M to the problem of learning cell dynamics from snapshot data. Notably, [SF]$^2$M is the first method to accurately model cell dynamics in high dimensions and can recover known gene regulatory networks from simulated data.

No Wrong Turns: The Simple Geometry Of Neural Networks Optimization Paths

Understanding the optimization dynamics of neural networks is necessary for closing the gap between theory and practice. Stochastic first-order optimization algorithms are known to efficiently locate favorable minima in deep neural networks. This efficiency, however, contrasts with the non-convex and seemingly complex structure of neural loss landscapes. In this study, we delve into the fundamental geometric properties of sampled gradients along optimization paths. We focus on two key quantities, which appear in the restricted secant inequality and error bound. Both hold high significance for first-order optimization. Our analysis reveals that these quantities exhibit predictable, consistent behavior throughout training, despite the stochasticity induced by sampling minibatches. Our findings suggest that not only do optimization trajectories never encounter significant obstacles, but they also maintain stable dynamics during the majority of training. These observed properties are sufficiently expressive to theoretically guarantee linear convergence and prescribe learning rate schedules mirroring empirical practices. We conduct our experiments on image classification, semantic segmentation and language modeling across different batch sizes, network architectures, datasets, optimizers, and initialization seeds. We discuss the impact of each factor. Our work provides novel insights into the properties of neural network loss functions, and opens the door to theoretical frameworks more relevant to prevalent practice.

Unbalanced Optimal Transport meets Sliced-Wasserstein

Optimal transport (OT) has emerged as a powerful framework to compare probability measures, a fundamental task in many statistical and machine learning problems. Substantial advances have been made over the last decade in designing OT variants which are either computationally and statistically more efficient, or more robust to the measures and datasets to compare. Among them, sliced OT distances have been extensively used to mitigate optimal transport's cubic algorithmic complexity and curse of dimensionality. In parallel, unbalanced OT was designed to allow comparisons of more general positive measures, while being more robust to outliers. In this paper, we propose to combine these two concepts, namely slicing and unbalanced OT, to develop a general framework for efficiently comparing positive measures. We propose two new loss functions based on the idea of slicing unbalanced OT, and study their induced topology and statistical properties. We then develop a fast Frank-Wolfe-type algorithm to compute these loss functions, and show that the resulting methodology is modular as it encompasses and extends prior related work. We finally conduct an empirical analysis of our loss functions and methodology on both synthetic and real datasets, to illustrate their relevance and applicability.

Diffusion models with location-scale noise

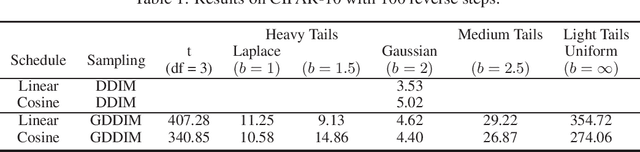
Diffusion Models (DMs) are powerful generative models that add Gaussian noise to the data and learn to remove it. We wanted to determine which noise distribution (Gaussian or non-Gaussian) led to better generated data in DMs. Since DMs do not work by design with non-Gaussian noise, we built a framework that allows reversing a diffusion process with non-Gaussian location-scale noise. We use that framework to show that the Gaussian distribution performs the best over a wide range of other distributions (Laplace, Uniform, t, Generalized-Gaussian).

PopulAtion Parameter Averaging (PAPA)

Ensemble methods combine the predictions of multiple models to improve performance, but they require significantly higher computation costs at inference time. To avoid these costs, multiple neural networks can be combined into one by averaging their weights (model soups). However, this usually performs significantly worse than ensembling. Weight averaging is only beneficial when weights are similar enough (in weight or feature space) to average well but different enough to benefit from combining them. Based on this idea, we propose PopulAtion Parameter Averaging (PAPA): a method that combines the generality of ensembling with the efficiency of weight averaging. PAPA leverages a population of diverse models (trained on different data orders, augmentations, and regularizations) while occasionally (not too often, not too rarely) replacing the weights of the networks with the population average of the weights. PAPA reduces the performance gap between averaging and ensembling, increasing the average accuracy of a population of models by up to 1.1% on CIFAR-10, 2.4% on CIFAR-100, and 1.9% on ImageNet when compared to training independent (non-averaged) models.

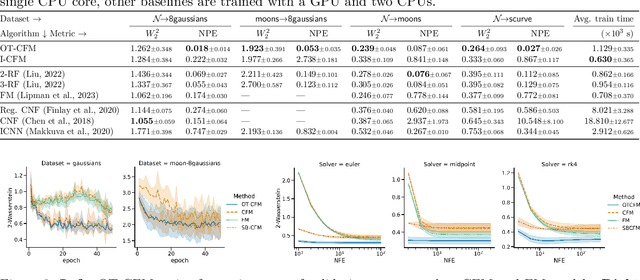
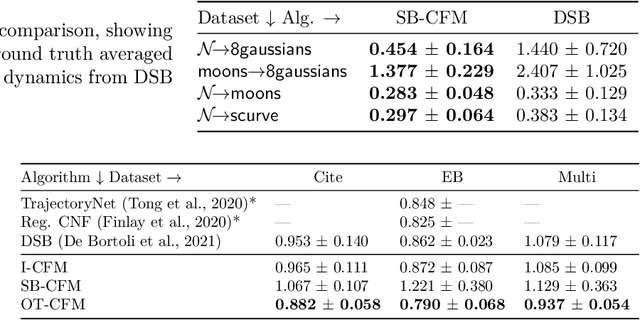
Conditional Flow Matching: Simulation-Free Dynamic Optimal Transport

Continuous normalizing flows (CNFs) are an attractive generative modeling technique, but they have thus far been held back by limitations in their simulation-based maximum likelihood training. In this paper, we introduce a new technique called conditional flow matching (CFM), a simulation-free training objective for CNFs. CFM features a stable regression objective like that used to train the stochastic flow in diffusion models but enjoys the efficient inference of deterministic flow models. In contrast to both diffusion models and prior CNF training algorithms, our CFM objective does not require the source distribution to be Gaussian or require evaluation of its density. Based on this new objective, we also introduce optimal transport CFM (OT-CFM), which creates simpler flows that are more stable to train and lead to faster inference, as evaluated in our experiments. Training CNFs with CFM improves results on a variety of conditional and unconditional generation tasks such as inferring single cell dynamics, unsupervised image translation, and Schr\"odinger bridge inference. Code is available at https://github.com/atong01/conditional-flow-matching .

A Reproducible and Realistic Evaluation of Partial Domain Adaptation Methods

Unsupervised Domain Adaptation (UDA) aims at classifying unlabeled target images leveraging source labeled ones. In this work, we consider the Partial Domain Adaptation (PDA) variant, where we have extra source classes not present in the target domain. Most successful algorithms use model selection strategies that rely on target labels to find the best hyper-parameters and/or models along training. However, these strategies violate the main assumption in PDA: only unlabeled target domain samples are available. Moreover, there are also inconsistencies in the experimental settings - architecture, hyper-parameter tuning, number of runs - yielding unfair comparisons. The main goal of this work is to provide a realistic evaluation of PDA methods with the different model selection strategies under a consistent evaluation protocol. We evaluate 7 representative PDA algorithms on 2 different real-world datasets using 7 different model selection strategies. Our two main findings are: (i) without target labels for model selection, the accuracy of the methods decreases up to 30 percentage points; (ii) only one method and model selection pair performs well on both datasets. Experiments were performed with our PyTorch framework, BenchmarkPDA, which we open source.