Addressing Sample Inefficiency in Multi-View Representation Learning

Non-contrastive self-supervised learning (NC-SSL) methods like BarlowTwins and VICReg have shown great promise for label-free representation learning in computer vision. Despite the apparent simplicity of these techniques, researchers must rely on several empirical heuristics to achieve competitive performance, most notably using high-dimensional projector heads and two augmentations of the same image. In this work, we provide theoretical insights on the implicit bias of the BarlowTwins and VICReg loss that can explain these heuristics and guide the development of more principled recommendations. Our first insight is that the orthogonality of the features is more critical than projector dimensionality for learning good representations. Based on this, we empirically demonstrate that low-dimensional projector heads are sufficient with appropriate regularization, contrary to the existing heuristic. Our second theoretical insight suggests that using multiple data augmentations better represents the desiderata of the SSL objective. Based on this, we demonstrate that leveraging more augmentations per sample improves representation quality and trainability. In particular, it improves optimization convergence, leading to better features emerging earlier in the training. Remarkably, we demonstrate that we can reduce the pretraining dataset size by up to 4x while maintaining accuracy and improving convergence simply by using more data augmentations. Combining these insights, we present practical pretraining recommendations that improve wall-clock time by 2x and improve performance on CIFAR-10/STL-10 datasets using a ResNet-50 backbone. Thus, this work provides a theoretical insight into NC-SSL and produces practical recommendations for enhancing its sample and compute efficiency.

EuclidNets: An Alternative Operation for Efficient Inference of Deep Learning Models

With the advent of deep learning application on edge devices, researchers actively try to optimize their deployments on low-power and restricted memory devices. There are established compression method such as quantization, pruning, and architecture search that leverage commodity hardware. Apart from conventional compression algorithms, one may redesign the operations of deep learning models that lead to more efficient implementation. To this end, we propose EuclidNet, a compression method, designed to be implemented on hardware which replaces multiplication, $xw$, with Euclidean distance $(x-w)^2$. We show that EuclidNet is aligned with matrix multiplication and it can be used as a measure of similarity in case of convolutional layers. Furthermore, we show that under various transformations and noise scenarios, EuclidNet exhibits the same performance compared to the deep learning models designed with multiplication operations.

A Reproducible and Realistic Evaluation of Partial Domain Adaptation Methods

Unsupervised Domain Adaptation (UDA) aims at classifying unlabeled target images leveraging source labeled ones. In this work, we consider the Partial Domain Adaptation (PDA) variant, where we have extra source classes not present in the target domain. Most successful algorithms use model selection strategies that rely on target labels to find the best hyper-parameters and/or models along training. However, these strategies violate the main assumption in PDA: only unlabeled target domain samples are available. Moreover, there are also inconsistencies in the experimental settings - architecture, hyper-parameter tuning, number of runs - yielding unfair comparisons. The main goal of this work is to provide a realistic evaluation of PDA methods with the different model selection strategies under a consistent evaluation protocol. We evaluate 7 representative PDA algorithms on 2 different real-world datasets using 7 different model selection strategies. Our two main findings are: (i) without target labels for model selection, the accuracy of the methods decreases up to 30 percentage points; (ii) only one method and model selection pair performs well on both datasets. Experiments were performed with our PyTorch framework, BenchmarkPDA, which we open source.

On the Generalization of Representations in Reinforcement Learning

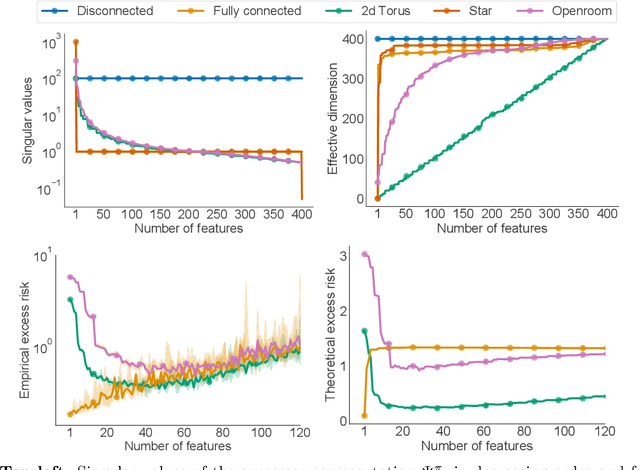
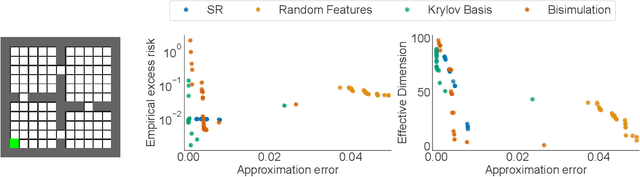
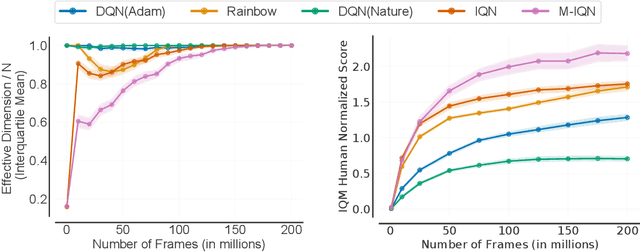
In reinforcement learning, state representations are used to tractably deal with large problem spaces. State representations serve both to approximate the value function with few parameters, but also to generalize to newly encountered states. Their features may be learned implicitly (as part of a neural network) or explicitly (for example, the successor representation of \citet{dayan1993improving}). While the approximation properties of representations are reasonably well-understood, a precise characterization of how and when these representations generalize is lacking. In this work, we address this gap and provide an informative bound on the generalization error arising from a specific state representation. This bound is based on the notion of effective dimension which measures the degree to which knowing the value at one state informs the value at other states. Our bound applies to any state representation and quantifies the natural tension between representations that generalize well and those that approximate well. We complement our theoretical results with an empirical survey of classic representation learning methods from the literature and results on the Arcade Learning Environment, and find that the generalization behaviour of learned representations is well-explained by their effective dimension.

Multi-Resolution Continuous Normalizing Flows

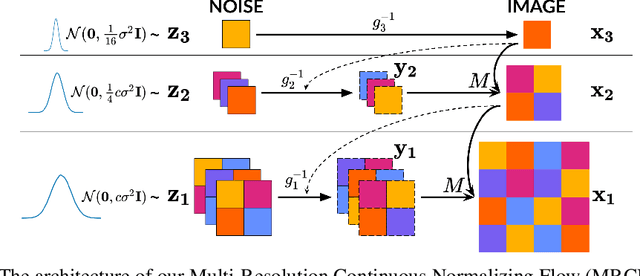
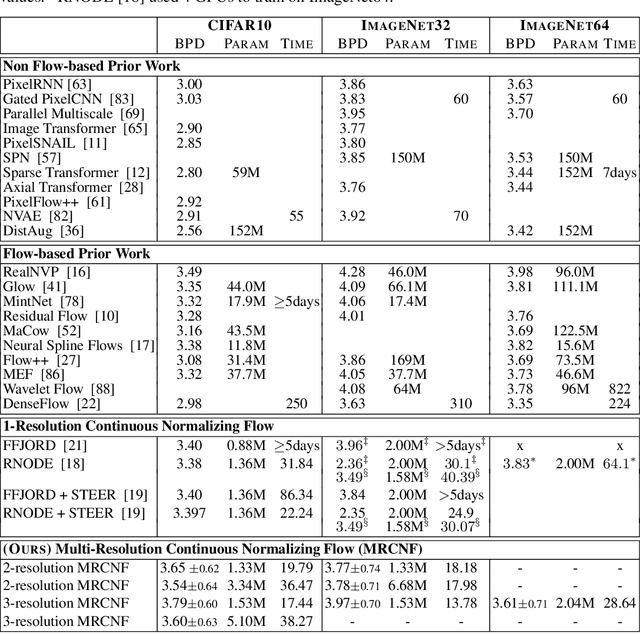
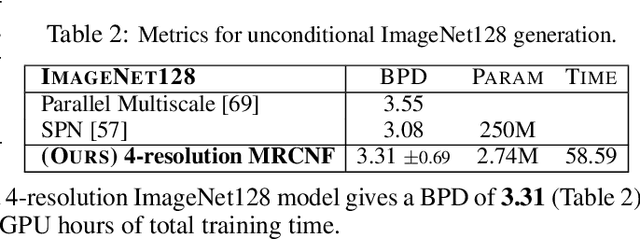
Recent work has shown that Neural Ordinary Differential Equations (ODEs) can serve as generative models of images using the perspective of Continuous Normalizing Flows (CNFs). Such models offer exact likelihood calculation, and invertible generation/density estimation. In this work we introduce a Multi-Resolution variant of such models (MRCNF), by characterizing the conditional distribution over the additional information required to generate a fine image that is consistent with the coarse image. We introduce a transformation between resolutions that allows for no change in the log likelihood. We show that this approach yields comparable likelihood values for various image datasets, with improved performance at higher resolutions, with fewer parameters, using only 1 GPU. Further, we examine the out-of-distribution properties of (Multi-Resolution) Continuous Normalizing Flows, and find that they are similar to those of other likelihood-based generative models.

Improved Predictive Uncertainty using Corruption-based Calibration

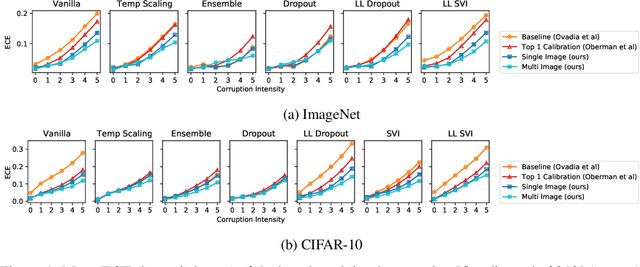
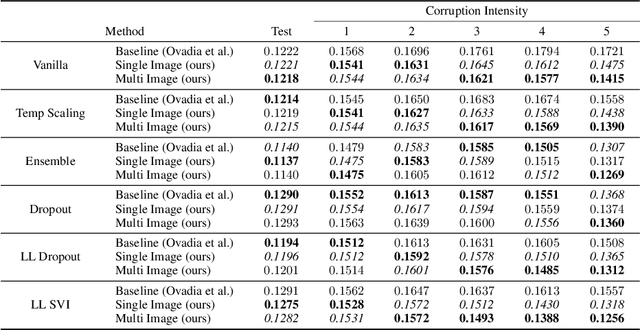
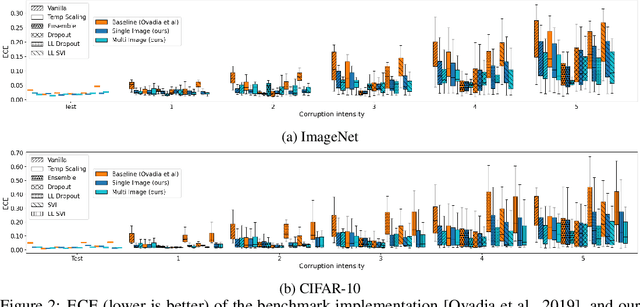
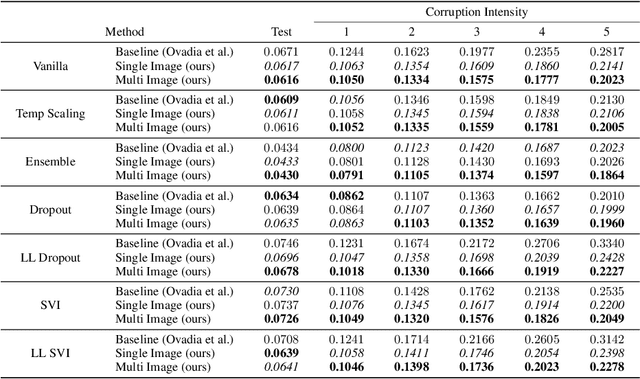
We propose a simple post hoc calibration method to estimate the confidence/uncertainty that a model prediction is correct on data with covariate shift, as represented by the large-scale corrupted data benchmark [Ovadia et al, 2019]. We achieve this by synthesizing surrogate calibration sets by corrupting the calibration set with varying intensities of a known corruption. Our method demonstrates significant improvements on the benchmark on a wide range of covariate shifts.

Bias Mitigation of Face Recognition Models Through Calibration

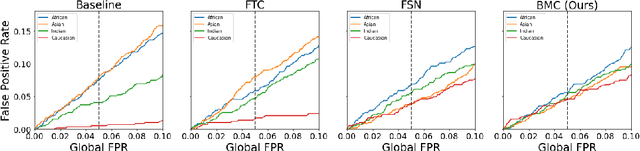
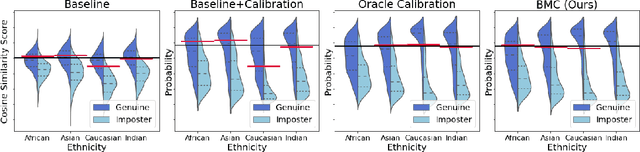
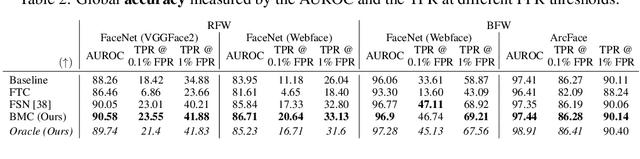
Face recognition models suffer from bias: for example, the probability of a false positive (incorrect face match) strongly depends on sensitive attributes like ethnicity. As a result, these models may disproportionately and negatively impact minority groups when used in law enforcement. In this work, we introduce the Bias Mitigation Calibration (BMC) method, which (i) increases model accuracy (improving the state-of-the-art), (ii) produces fairly-calibrated probabilities, (iii) significantly reduces the gap in the false positive rates, and (iv) does not require knowledge of the sensitive attribute.

A principled approach for generating adversarial images under non-smooth dissimilarity metrics

Deep neural networks are vulnerable to adversarial perturbations: small changes in the input easily lead to misclassification. In this work, we propose an attack methodology catered not only for cases where the perturbations are measured by $\ell_p$ norms, but in fact any adversarial dissimilarity metric with a closed proximal form. This includes, but is not limited to, $\ell_1$, $\ell_2$, $\ell_\infty$ perturbations, and the $\ell_0$ counting "norm", i.e. true sparseness. Our approach to generating perturbations is a natural extension of our recent work, the LogBarrier attack, which previously required the metric to be differentiable. We demonstrate our new algorithm, ProxLogBarrier, on the MNIST, CIFAR10, and ImageNet-1k datasets. We attack undefended and defended models, and show that our algorithm transfers to various datasets with little parameter tuning. In particular, in the $\ell_0$ case, our algorithm finds significantly smaller perturbations compared to multiple existing methods

Improved robustness to adversarial examples using Lipschitz regularization of the loss

Adversarial training is an effective method for improving robustness to adversarial attacks. We show that adversarial training using the Fast Signed Gradient Method can be interpreted as a form of regularization. We implemented a more effective form of adversarial training, which in turn can be interpreted as regularization of the loss in the 2-norm, $\|\nabla_x \ell(x)\|_2$. We obtained further improvements to adversarial robustness, as well as provable robustness guarantees, by augmenting adversarial training with Lipschitz regularization.

Stochastic Backward Euler: An Implicit Gradient Descent Algorithm for $k$-means Clustering

In this paper, we propose an implicit gradient descent algorithm for the classic $k$-means problem. The implicit gradient step or backward Euler is solved via stochastic fixed-point iteration, in which we randomly sample a mini-batch gradient in every iteration. It is the average of the fixed-point trajectory that is carried over to the next gradient step. We draw connections between the proposed stochastic backward Euler and the recent entropy stochastic gradient descent (Entropy-SGD) for improving the training of deep neural networks. Numerical experiments on various synthetic and real datasets show that the proposed algorithm provides better clustering results compared to $k$-means algorithms in the sense that it decreased the objective function (the cluster) and is much more robust to initialization.