Weight-Sharing Regularization

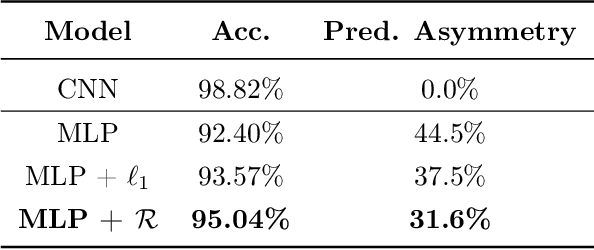
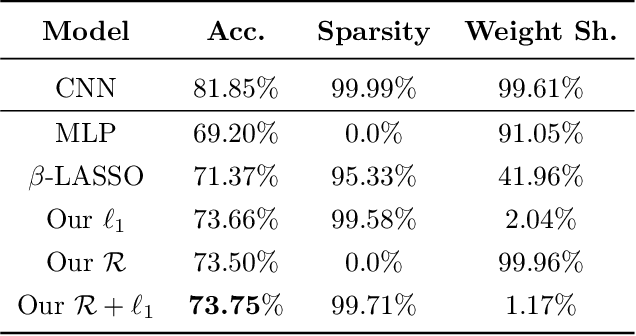
Weight-sharing is ubiquitous in deep learning. Motivated by this, we introduce ''weight-sharing regularization'' for neural networks, defined as $R(w) = \frac{1}{d - 1}\sum_{i > j}^d |w_i - w_j|$. We study the proximal mapping of $R$ and provide an intuitive interpretation of it in terms of a physical system of interacting particles. Using this interpretation, we design a novel parallel algorithm for $\operatorname{prox}_R$ which provides an exponential speedup over previous algorithms, with a depth of $O(\log^3 d)$. Our algorithm makes it feasible to train weight-sharing regularized deep neural networks with proximal gradient descent. Experiments reveal that weight-sharing regularization enables fully-connected networks to learn convolution-like filters.

Utility Theory for Sequential Decision Making

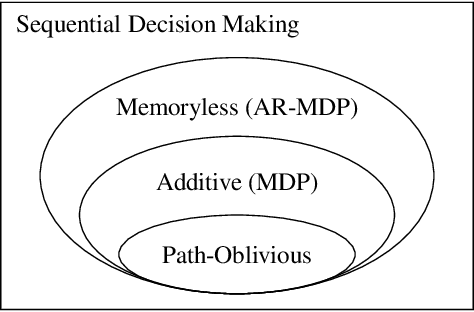
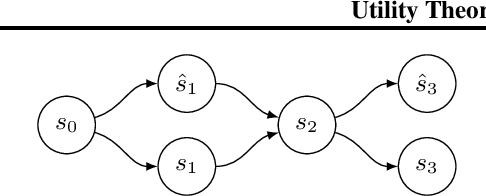
The von Neumann-Morgenstern (VNM) utility theorem shows that under certain axioms of rationality, decision-making is reduced to maximizing the expectation of some utility function. We extend these axioms to increasingly structured sequential decision making settings and identify the structure of the corresponding utility functions. In particular, we show that memoryless preferences lead to a utility in the form of a per transition reward and multiplicative factor on the future return. This result motivates a generalization of Markov Decision Processes (MDPs) with this structure on the agent's returns, which we call Affine-Reward MDPs. A stronger constraint on preferences is needed to recover the commonly used cumulative sum of scalar rewards in MDPs. A yet stronger constraint simplifies the utility function for goal-seeking agents in the form of a difference in some function of states that we call potential functions. Our necessary and sufficient conditions demystify the reward hypothesis that underlies the design of rational agents in reinforcement learning by adding an axiom to the VNM rationality axioms and motivates new directions for AI research involving sequential decision making.

Transformation Coding: Simple Objectives for Equivariant Representations

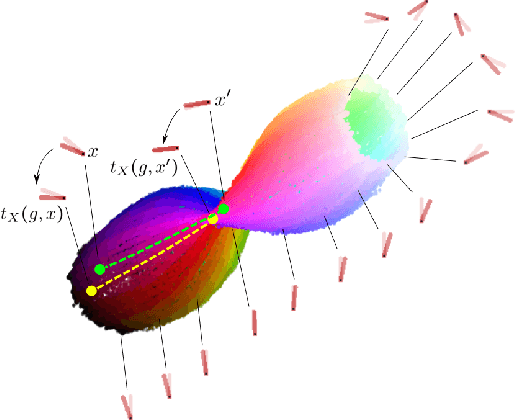
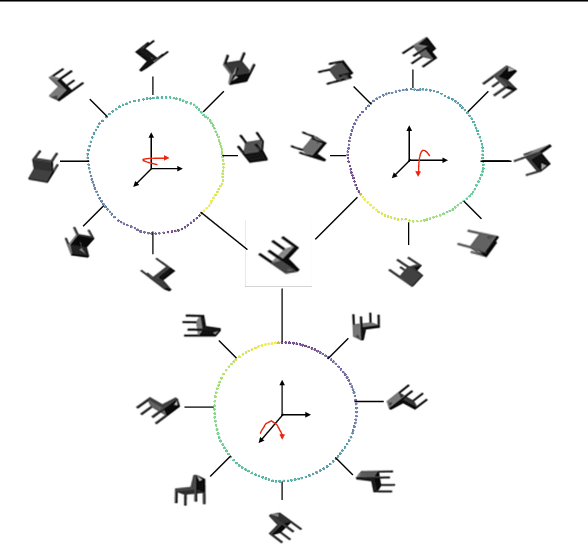
We present a simple non-generative approach to deep representation learning that seeks equivariant deep embedding through simple objectives. In contrast to existing equivariant networks, our transformation coding approach does not constrain the choice of the feed-forward layer or the architecture and allows for an unknown group action on the input space. We introduce several such transformation coding objectives for different Lie groups such as the Euclidean, Orthogonal and the Unitary groups. When using product groups, the representation is decomposed and disentangled. We show that the presence of additional information on different transformations improves disentanglement in transformation coding. We evaluate the representations learnt by transformation coding both qualitatively and quantitatively on downstream tasks, including reinforcement learning.

Equivariant Networks for Pixelized Spheres

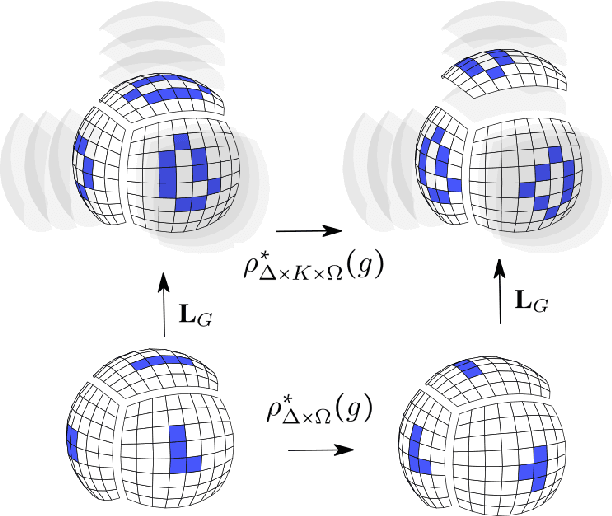
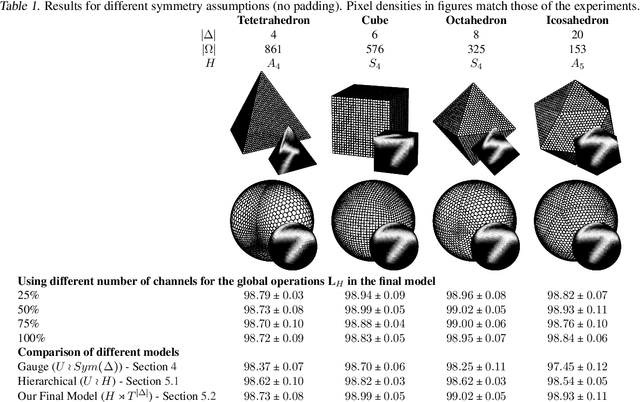
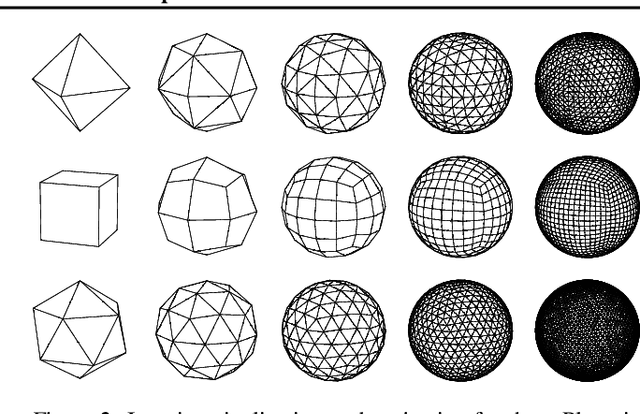
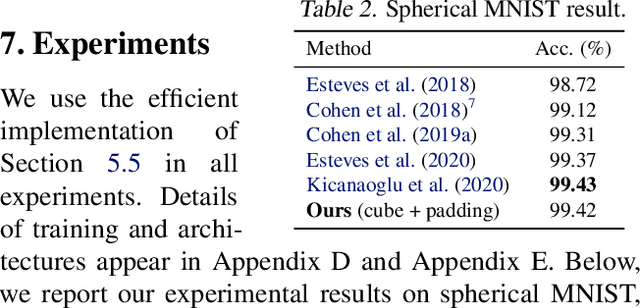
Pixelizations of Platonic solids such as the cube and icosahedron have been widely used to represent spherical data, from climate records to Cosmic Microwave Background maps. Platonic solids have well-known global symmetries. Once we pixelize each face of the solid, each face also possesses its own local symmetries in the form of Euclidean isometries. One way to combine these symmetries is through a hierarchy. However, this approach does not adequately model the interplay between the two levels of symmetry transformations. We show how to model this interplay using ideas from group theory, identify the equivariant linear maps, and introduce equivariant padding that respects these symmetries. Deep networks that use these maps as their building blocks generalize gauge equivariant CNNs on pixelized spheres. These deep networks achieve state-of-the-art results on semantic segmentation for climate data and omnidirectional image processing. Code is available at https://git.io/JGiZA.