Transformation Coding: Simple Objectives for Equivariant Representations
Paper and Code
Feb 19, 2022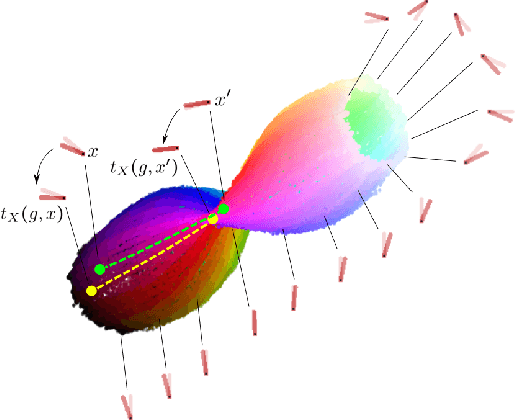

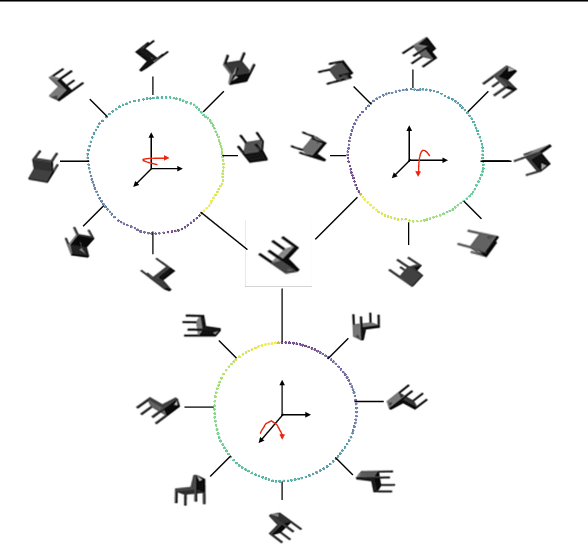

We present a simple non-generative approach to deep representation learning that seeks equivariant deep embedding through simple objectives. In contrast to existing equivariant networks, our transformation coding approach does not constrain the choice of the feed-forward layer or the architecture and allows for an unknown group action on the input space. We introduce several such transformation coding objectives for different Lie groups such as the Euclidean, Orthogonal and the Unitary groups. When using product groups, the representation is decomposed and disentangled. We show that the presence of additional information on different transformations improves disentanglement in transformation coding. We evaluate the representations learnt by transformation coding both qualitatively and quantitatively on downstream tasks, including reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge