Parity Requires Unified Input Dependence and Negative Eigenvalues in SSMs

Recent work has shown that LRNN models such as S4D, Mamba, and DeltaNet lack state-tracking capability due to either time-invariant transition matrices or restricted eigenvalue ranges. To address this, input-dependent transition matrices, particularly those that are complex or non-triangular, have been proposed to enhance SSM performance on such tasks. While existing theorems demonstrate that both input-independent and non-negative SSMs are incapable of solving simple state-tracking tasks, such as parity, regardless of depth, they do not explore whether combining these two types in a multilayer SSM could help. We investigate this question for efficient SSMs with diagonal transition matrices and show that such combinations still fail to solve parity. This implies that a recurrence layer must both be input-dependent and include negative eigenvalues. Our experiments support this conclusion by analyzing an SSM model that combines S4D and Mamba layers.

Diffusion Tree Sampling: Scalable inference-time alignment of diffusion models

Adapting a pretrained diffusion model to new objectives at inference time remains an open problem in generative modeling. Existing steering methods suffer from inaccurate value estimation, especially at high noise levels, which biases guidance. Moreover, information from past runs is not reused to improve sample quality, resulting in inefficient use of compute. Inspired by the success of Monte Carlo Tree Search, we address these limitations by casting inference-time alignment as a search problem that reuses past computations. We introduce a tree-based approach that samples from the reward-aligned target density by propagating terminal rewards back through the diffusion chain and iteratively refining value estimates with each additional generation. Our proposed method, Diffusion Tree Sampling (DTS), produces asymptotically exact samples from the target distribution in the limit of infinite rollouts, and its greedy variant, Diffusion Tree Search (DTS$^\star$), performs a global search for high reward samples. On MNIST and CIFAR-10 class-conditional generation, DTS matches the FID of the best-performing baseline with up to $10\times$ less compute. In text-to-image generation and language completion tasks, DTS$^\star$ effectively searches for high reward samples that match best-of-N with up to $5\times$ less compute. By reusing information from previous generations, we get an anytime algorithm that turns additional compute into steadily better samples, providing a scalable approach for inference-time alignment of diffusion models.

Beyond Scalar Rewards: An Axiomatic Framework for Lexicographic MDPs

Recent work has formalized the reward hypothesis through the lens of expected utility theory, by interpreting reward as utility. Hausner's foundational work showed that dropping the continuity axiom leads to a generalization of expected utility theory where utilities are lexicographically ordered vectors of arbitrary dimension. In this paper, we extend this result by identifying a simple and practical condition under which preferences cannot be represented by scalar rewards, necessitating a 2-dimensional reward function. We provide a full characterization of such reward functions, as well as the general d-dimensional case, in Markov Decision Processes (MDPs) under a memorylessness assumption on preferences. Furthermore, we show that optimal policies in this setting retain many desirable properties of their scalar-reward counterparts, while in the Constrained MDP (CMDP) setting -- another common multiobjective setting -- they do not.

On the Identifiability of Causal Abstractions

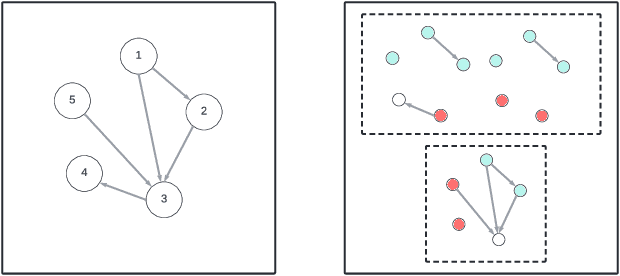
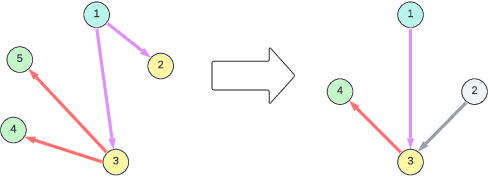
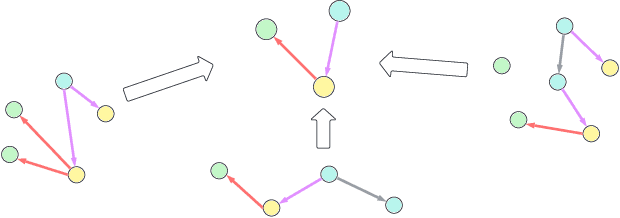
Causal representation learning (CRL) enhances machine learning models' robustness and generalizability by learning structural causal models associated with data-generating processes. We focus on a family of CRL methods that uses contrastive data pairs in the observable space, generated before and after a random, unknown intervention, to identify the latent causal model. (Brehmer et al., 2022) showed that this is indeed possible, given that all latent variables can be intervened on individually. However, this is a highly restrictive assumption in many systems. In this work, we instead assume interventions on arbitrary subsets of latent variables, which is more realistic. We introduce a theoretical framework that calculates the degree to which we can identify a causal model, given a set of possible interventions, up to an abstraction that describes the system at a higher level of granularity.

SymmCD: Symmetry-Preserving Crystal Generation with Diffusion Models

Generating novel crystalline materials has potential to lead to advancements in fields such as electronics, energy storage, and catalysis. The defining characteristic of crystals is their symmetry, which plays a central role in determining their physical properties. However, existing crystal generation methods either fail to generate materials that display the symmetries of real-world crystals, or simply replicate the symmetry information from examples in a database. To address this limitation, we propose SymmCD, a novel diffusion-based generative model that explicitly incorporates crystallographic symmetry into the generative process. We decompose crystals into two components and learn their joint distribution through diffusion: 1) the asymmetric unit, the smallest subset of the crystal which can generate the whole crystal through symmetry transformations, and; 2) the symmetry transformations needed to be applied to each atom in the asymmetric unit. We also use a novel and interpretable representation for these transformations, enabling generalization across different crystallographic symmetry groups. We showcase the competitive performance of SymmCD on a subset of the Materials Project, obtaining diverse and valid crystals with realistic symmetries and predicted properties.

Symmetry-Aware Generative Modeling through Learned Canonicalization

Generative modeling of symmetric densities has a range of applications in AI for science, from drug discovery to physics simulations. The existing generative modeling paradigm for invariant densities combines an invariant prior with an equivariant generative process. However, we observe that this technique is not necessary and has several drawbacks resulting from the limitations of equivariant networks. Instead, we propose to model a learned slice of the density so that only one representative element per orbit is learned. To accomplish this, we learn a group-equivariant canonicalization network that maps training samples to a canonical pose and train a non-equivariant generative model over these canonicalized samples. We implement this idea in the context of diffusion models. Our preliminary experimental results on molecular modeling are promising, demonstrating improved sample quality and faster inference time.

Sampling from Energy-based Policies using Diffusion

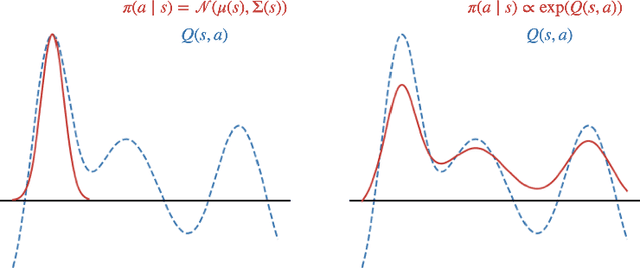
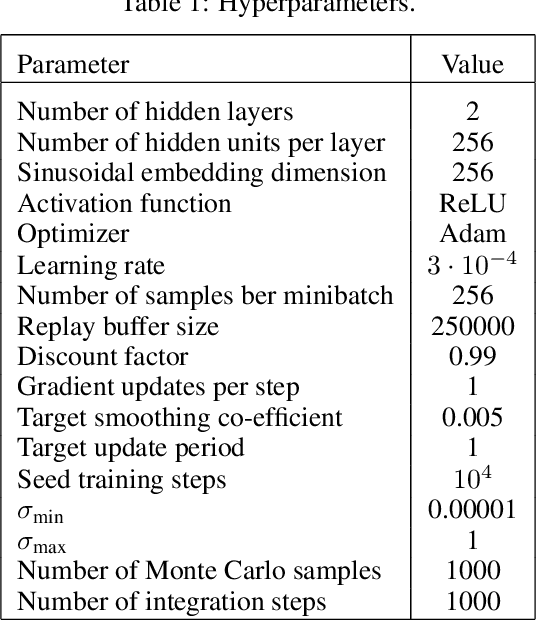
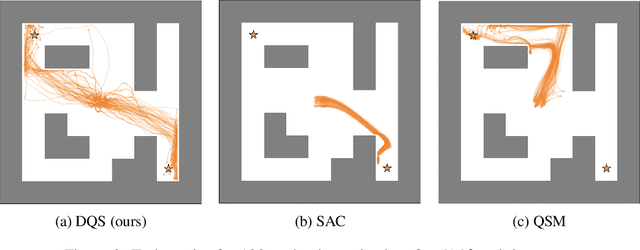
Energy-based policies offer a flexible framework for modeling complex, multimodal behaviors in reinforcement learning (RL). In maximum entropy RL, the optimal policy is a Boltzmann distribution derived from the soft Q-function, but direct sampling from this distribution in continuous action spaces is computationally intractable. As a result, existing methods typically use simpler parametric distributions, like Gaussians, for policy representation - limiting their ability to capture the full complexity of multimodal action distributions. In this paper, we introduce a diffusion-based approach for sampling from energy-based policies, where the negative Q-function defines the energy function. Based on this approach, we propose an actor-critic method called Diffusion Q-Sampling (DQS) that enables more expressive policy representations, allowing stable learning in diverse environments. We show that our approach enhances exploration and captures multimodal behavior in continuous control tasks, addressing key limitations of existing methods.

E(3)-Equivariant Mesh Neural Networks

Triangular meshes are widely used to represent three-dimensional objects. As a result, many recent works have address the need for geometric deep learning on 3D mesh. However, we observe that the complexities in many of these architectures does not translate to practical performance, and simple deep models for geometric graphs are competitive in practice. Motivated by this observation, we minimally extend the update equations of E(n)-Equivariant Graph Neural Networks (EGNNs) (Satorras et al., 2021) to incorporate mesh face information, and further improve it to account for long-range interactions through hierarchy. The resulting architecture, Equivariant Mesh Neural Network (EMNN), outperforms other, more complicated equivariant methods on mesh tasks, with a fast run-time and no expensive pre-processing. Our implementation is available at https://github.com/HySonLab/EquiMesh

Iterated Denoising Energy Matching for Sampling from Boltzmann Densities

Efficiently generating statistically independent samples from an unnormalized probability distribution, such as equilibrium samples of many-body systems, is a foundational problem in science. In this paper, we propose Iterated Denoising Energy Matching (iDEM), an iterative algorithm that uses a novel stochastic score matching objective leveraging solely the energy function and its gradient -- and no data samples -- to train a diffusion-based sampler. Specifically, iDEM alternates between (I) sampling regions of high model density from a diffusion-based sampler and (II) using these samples in our stochastic matching objective to further improve the sampler. iDEM is scalable to high dimensions as the inner matching objective, is simulation-free, and requires no MCMC samples. Moreover, by leveraging the fast mode mixing behavior of diffusion, iDEM smooths out the energy landscape enabling efficient exploration and learning of an amortized sampler. We evaluate iDEM on a suite of tasks ranging from standard synthetic energy functions to invariant $n$-body particle systems. We show that the proposed approach achieves state-of-the-art performance on all metrics and trains $2-5\times$ faster, which allows it to be the first method to train using energy on the challenging $55$-particle Lennard-Jones system.

Symmetry Breaking and Equivariant Neural Networks

Using symmetry as an inductive bias in deep learning has been proven to be a principled approach for sample-efficient model design. However, the relationship between symmetry and the imperative for equivariance in neural networks is not always obvious. Here, we analyze a key limitation that arises in equivariant functions: their incapacity to break symmetry at the level of individual data samples. In response, we introduce a novel notion of 'relaxed equivariance' that circumvents this limitation. We further demonstrate how to incorporate this relaxation into equivariant multilayer perceptrons (E-MLPs), offering an alternative to the noise-injection method. The relevance of symmetry breaking is then discussed in various application domains: physics, graph representation learning, combinatorial optimization and equivariant decoding.