SEMU: Singular Value Decomposition for Efficient Machine Unlearning

While the capabilities of generative foundational models have advanced rapidly in recent years, methods to prevent harmful and unsafe behaviors remain underdeveloped. Among the pressing challenges in AI safety, machine unlearning (MU) has become increasingly critical to meet upcoming safety regulations. Most existing MU approaches focus on altering the most significant parameters of the model. However, these methods often require fine-tuning substantial portions of the model, resulting in high computational costs and training instabilities, which are typically mitigated by access to the original training dataset. In this work, we address these limitations by leveraging Singular Value Decomposition (SVD) to create a compact, low-dimensional projection that enables the selective forgetting of specific data points. We propose Singular Value Decomposition for Efficient Machine Unlearning (SEMU), a novel approach designed to optimize MU in two key aspects. First, SEMU minimizes the number of model parameters that need to be modified, effectively removing unwanted knowledge while making only minimal changes to the model's weights. Second, SEMU eliminates the dependency on the original training dataset, preserving the model's previously acquired knowledge without additional data requirements. Extensive experiments demonstrate that SEMU achieves competitive performance while significantly improving efficiency in terms of both data usage and the number of modified parameters.

Outsourced diffusion sampling: Efficient posterior inference in latent spaces of generative models

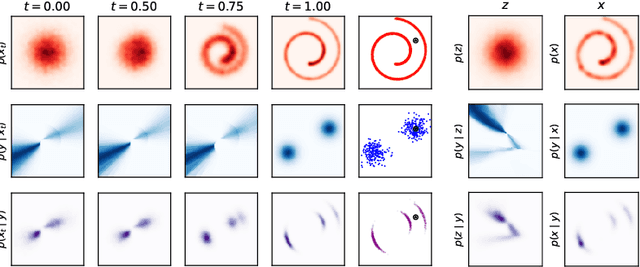
Any well-behaved generative model over a variable $\mathbf{x}$ can be expressed as a deterministic transformation of an exogenous ('outsourced') Gaussian noise variable $\mathbf{z}$: $\mathbf{x}=f_\theta(\mathbf{z})$. In such a model (e.g., a VAE, GAN, or continuous-time flow-based model), sampling of the target variable $\mathbf{x} \sim p_\theta(\mathbf{x})$ is straightforward, but sampling from a posterior distribution of the form $p(\mathbf{x}\mid\mathbf{y}) \propto p_\theta(\mathbf{x})r(\mathbf{x},\mathbf{y})$, where $r$ is a constraint function depending on an auxiliary variable $\mathbf{y}$, is generally intractable. We propose to amortize the cost of sampling from such posterior distributions with diffusion models that sample a distribution in the noise space ($\mathbf{z}$). These diffusion samplers are trained by reinforcement learning algorithms to enforce that the transformed samples $f_\theta(\mathbf{z})$ are distributed according to the posterior in the data space ($\mathbf{x}$). For many models and constraints of interest, the posterior in the noise space is smoother than the posterior in the data space, making it more amenable to such amortized inference. Our method enables conditional sampling under unconditional GAN, (H)VAE, and flow-based priors, comparing favorably both with current amortized and non-amortized inference methods. We demonstrate the proposed outsourced diffusion sampling in several experiments with large pretrained prior models: conditional image generation, reinforcement learning with human feedback, and protein structure generation.

From discrete-time policies to continuous-time diffusion samplers: Asymptotic equivalences and faster training

We study the problem of training neural stochastic differential equations, or diffusion models, to sample from a Boltzmann distribution without access to target samples. Existing methods for training such models enforce time-reversal of the generative and noising processes, using either differentiable simulation or off-policy reinforcement learning (RL). We prove equivalences between families of objectives in the limit of infinitesimal discretization steps, linking entropic RL methods (GFlowNets) with continuous-time objects (partial differential equations and path space measures). We further show that an appropriate choice of coarse time discretization during training allows greatly improved sample efficiency and the use of time-local objectives, achieving competitive performance on standard sampling benchmarks with reduced computational cost.

High-Fidelity Transfer of Functional Priors for Wide Bayesian Neural Networks by Learning Activations

Function-space priors in Bayesian Neural Networks provide a more intuitive approach to embedding beliefs directly into the model's output, thereby enhancing regularization, uncertainty quantification, and risk-aware decision-making. However, imposing function-space priors on BNNs is challenging. We address this task through optimization techniques that explore how trainable activations can accommodate complex priors and match intricate target function distributions. We discuss critical learning challenges, including identifiability, loss construction, and symmetries that arise in this context. Furthermore, we enable evidence maximization to facilitate model selection by conditioning the functional priors on additional hyperparameters. Our empirical findings demonstrate that even BNNs with a single wide hidden layer, when equipped with these adaptive trainable activations and conditioning strategies, can effectively achieve high-fidelity function-space priors, providing a robust and flexible framework for enhancing Bayesian neural network performance.

AutoLoRA: AutoGuidance Meets Low-Rank Adaptation for Diffusion Models

Low-rank adaptation (LoRA) is a fine-tuning technique that can be applied to conditional generative diffusion models. LoRA utilizes a small number of context examples to adapt the model to a specific domain, character, style, or concept. However, due to the limited data utilized during training, the fine-tuned model performance is often characterized by strong context bias and a low degree of variability in the generated images. To solve this issue, we introduce AutoLoRA, a novel guidance technique for diffusion models fine-tuned with the LoRA approach. Inspired by other guidance techniques, AutoLoRA searches for a trade-off between consistency in the domain represented by LoRA weights and sample diversity from the base conditional diffusion model. Moreover, we show that incorporating classifier-free guidance for both LoRA fine-tuned and base models leads to generating samples with higher diversity and better quality. The experimental results for several fine-tuned LoRA domains show superiority over existing guidance techniques on selected metrics.

Amortizing intractable inference in diffusion models for vision, language, and control

Diffusion models have emerged as effective distribution estimators in vision, language, and reinforcement learning, but their use as priors in downstream tasks poses an intractable posterior inference problem. This paper studies amortized sampling of the posterior over data, $\mathbf{x}\sim p^{\rm post}(\mathbf{x})\propto p(\mathbf{x})r(\mathbf{x})$, in a model that consists of a diffusion generative model prior $p(\mathbf{x})$ and a black-box constraint or likelihood function $r(\mathbf{x})$. We state and prove the asymptotic correctness of a data-free learning objective, relative trajectory balance, for training a diffusion model that samples from this posterior, a problem that existing methods solve only approximately or in restricted cases. Relative trajectory balance arises from the generative flow network perspective on diffusion models, which allows the use of deep reinforcement learning techniques to improve mode coverage. Experiments illustrate the broad potential of unbiased inference of arbitrary posteriors under diffusion priors: in vision (classifier guidance), language (infilling under a discrete diffusion LLM), and multimodal data (text-to-image generation). Beyond generative modeling, we apply relative trajectory balance to the problem of continuous control with a score-based behavior prior, achieving state-of-the-art results on benchmarks in offline reinforcement learning.

On diffusion models for amortized inference: Benchmarking and improving stochastic control and sampling

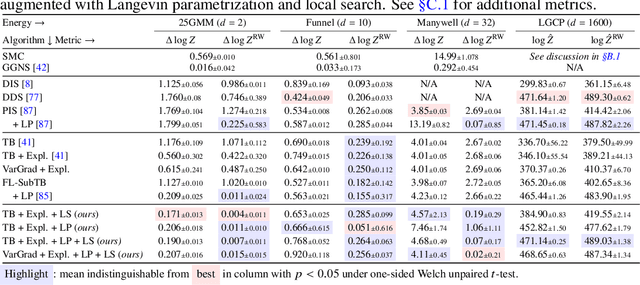
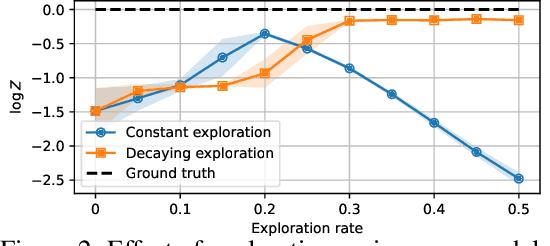
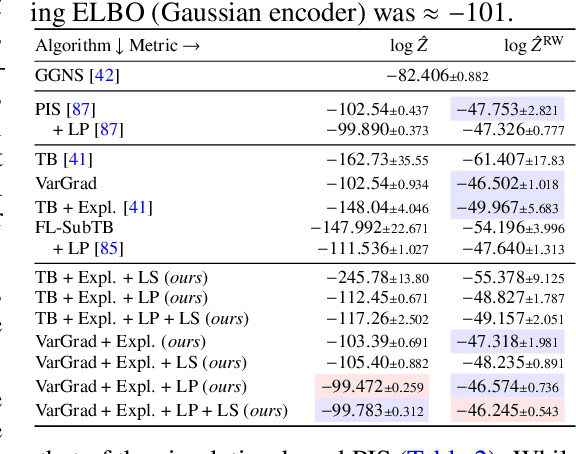
We study the problem of training diffusion models to sample from a distribution with a given unnormalized density or energy function. We benchmark several diffusion-structured inference methods, including simulation-based variational approaches and off-policy methods (continuous generative flow networks). Our results shed light on the relative advantages of existing algorithms while bringing into question some claims from past work. We also propose a novel exploration strategy for off-policy methods, based on local search in the target space with the use of a replay buffer, and show that it improves the quality of samples on a variety of target distributions. Our code for the sampling methods and benchmarks studied is made public at https://github.com/GFNOrg/gfn-diffusion as a base for future work on diffusion models for amortized inference.

Iterated Denoising Energy Matching for Sampling from Boltzmann Densities

Efficiently generating statistically independent samples from an unnormalized probability distribution, such as equilibrium samples of many-body systems, is a foundational problem in science. In this paper, we propose Iterated Denoising Energy Matching (iDEM), an iterative algorithm that uses a novel stochastic score matching objective leveraging solely the energy function and its gradient -- and no data samples -- to train a diffusion-based sampler. Specifically, iDEM alternates between (I) sampling regions of high model density from a diffusion-based sampler and (II) using these samples in our stochastic matching objective to further improve the sampler. iDEM is scalable to high dimensions as the inner matching objective, is simulation-free, and requires no MCMC samples. Moreover, by leveraging the fast mode mixing behavior of diffusion, iDEM smooths out the energy landscape enabling efficient exploration and learning of an amortized sampler. We evaluate iDEM on a suite of tasks ranging from standard synthetic energy functions to invariant $n$-body particle systems. We show that the proposed approach achieves state-of-the-art performance on all metrics and trains $2-5\times$ faster, which allows it to be the first method to train using energy on the challenging $55$-particle Lennard-Jones system.

HyperShot: Few-Shot Learning by Kernel HyperNetworks

Few-shot models aim at making predictions using a minimal number of labeled examples from a given task. The main challenge in this area is the one-shot setting where only one element represents each class. We propose HyperShot - the fusion of kernels and hypernetwork paradigm. Compared to reference approaches that apply a gradient-based adjustment of the parameters, our model aims to switch the classification module parameters depending on the task's embedding. In practice, we utilize a hypernetwork, which takes the aggregated information from support data and returns the classifier's parameters handcrafted for the considered problem. Moreover, we introduce the kernel-based representation of the support examples delivered to hypernetwork to create the parameters of the classification module. Consequently, we rely on relations between embeddings of the support examples instead of direct feature values provided by the backbone models. Thanks to this approach, our model can adapt to highly different tasks.

Non-Gaussian Gaussian Processes for Few-Shot Regression

Gaussian Processes (GPs) have been widely used in machine learning to model distributions over functions, with applications including multi-modal regression, time-series prediction, and few-shot learning. GPs are particularly useful in the last application since they rely on Normal distributions and enable closed-form computation of the posterior probability function. Unfortunately, because the resulting posterior is not flexible enough to capture complex distributions, GPs assume high similarity between subsequent tasks - a requirement rarely met in real-world conditions. In this work, we address this limitation by leveraging the flexibility of Normalizing Flows to modulate the posterior predictive distribution of the GP. This makes the GP posterior locally non-Gaussian, therefore we name our method Non-Gaussian Gaussian Processes (NGGPs). More precisely, we propose an invertible ODE-based mapping that operates on each component of the random variable vectors and shares the parameters across all of them. We empirically tested the flexibility of NGGPs on various few-shot learning regression datasets, showing that the mapping can incorporate context embedding information to model different noise levels for periodic functions. As a result, our method shares the structure of the problem between subsequent tasks, but the contextualization allows for adaptation to dissimilarities. NGGPs outperform the competing state-of-the-art approaches on a diversified set of benchmarks and applications.