Operator Learning Using Weak Supervision from Walk-on-Spheres

Training neural PDE solvers is often bottlenecked by expensive data generation or unstable physics-informed neural network (PINN) involving challenging optimization landscapes due to higher-order derivatives. To tackle this issue, we propose an alternative approach using Monte Carlo approaches to estimate the solution to the PDE as a stochastic process for weak supervision during training. Leveraging the Walk-on-Spheres method, we introduce a learning scheme called \emph{Walk-on-Spheres Neural Operator (WoS-NO)} which uses weak supervision from WoS to train any given neural operator. We propose to amortize the cost of Monte Carlo walks across the distribution of PDE instances using stochastic representations from the WoS algorithm to generate cheap, noisy, estimates of the PDE solution during training. This is formulated into a data-free physics-informed objective where a neural operator is trained to regress against these weak supervisions, allowing the operator to learn a generalized solution map for an entire family of PDEs. This strategy does not require expensive pre-computed datasets, avoids computing higher-order derivatives for loss functions that are memory-intensive and unstable, and demonstrates zero-shot generalization to novel PDE parameters and domains. Experiments show that for the same number of training steps, our method exhibits up to 8.75$\times$ improvement in $L_2$-error compared to standard physics-informed training schemes, up to 6.31$\times$ improvement in training speed, and reductions of up to 2.97$\times$ in GPU memory consumption. We present the code at https://github.com/neuraloperator/WoS-NO

Bridge Matching Sampler: Scalable Sampling via Generalized Fixed-Point Diffusion Matching

Sampling from unnormalized densities using diffusion models has emerged as a powerful paradigm. However, while recent approaches that use least-squares `matching' objectives have improved scalability, they often necessitate significant trade-offs, such as restricting prior distributions or relying on unstable optimization schemes. By generalizing these methods as special forms of fixed-point iterations rooted in Nelson's relation, we develop a new method that addresses these limitations, called Bridge Matching Sampler (BMS). Our approach enables learning a stochastic transport map between arbitrary prior and target distributions with a single, scalable, and stable objective. Furthermore, we introduce a damped variant of this iteration that incorporates a regularization term to mitigate mode collapse and further stabilize training. Empirically, we demonstrate that our method enables sampling at unprecedented scales while preserving mode diversity, achieving state-of-the-art results on complex synthetic densities and high-dimensional molecular benchmarks.

Mode Seeking meets Mean Seeking for Fast Long Video Generation

Scaling video generation from seconds to minutes faces a critical bottleneck: while short-video data is abundant and high-fidelity, coherent long-form data is scarce and limited to narrow domains. To address this, we propose a training paradigm where Mode Seeking meets Mean Seeking, decoupling local fidelity from long-term coherence based on a unified representation via a Decoupled Diffusion Transformer. Our approach utilizes a global Flow Matching head trained via supervised learning on long videos to capture narrative structure, while simultaneously employing a local Distribution Matching head that aligns sliding windows to a frozen short-video teacher via a mode-seeking reverse-KL divergence. This strategy enables the synthesis of minute-scale videos that learns long-range coherence and motions from limited long videos via supervised flow matching, while inheriting local realism by aligning every sliding-window segment of the student to a frozen short-video teacher, resulting in a few-step fast long video generator. Evaluations show that our method effectively closes the fidelity-horizon gap by jointly improving local sharpness, motion and long-range consistency. Project website: https://primecai.github.io/mmm/.

Self-Supervised Learning via Flow-Guided Neural Operator on Time-Series Data

Self-supervised learning (SSL) is a powerful paradigm for learning from unlabeled time-series data. However, popular methods such as masked autoencoders (MAEs) rely on reconstructing inputs from a fixed, predetermined masking ratio. Instead of this static design, we propose treating the corruption level as a new degree of freedom for representation learning, enhancing flexibility and performance. To achieve this, we introduce the Flow-Guided Neural Operator (FGNO), a novel framework combining operator learning with flow matching for SSL training. FGNO learns mappings in functional spaces by using Short-Time Fourier Transform to unify different time resolutions. We extract a rich hierarchy of features by tapping into different network layers and flow times that apply varying strengths of noise to the input data. This enables the extraction of versatile representations, from low-level patterns to high-level global features, using a single model adaptable to specific tasks. Unlike prior generative SSL methods that use noisy inputs during inference, we propose using clean inputs for representation extraction while learning representations with noise; this eliminates randomness and boosts accuracy. We evaluate FGNO across three biomedical domains, where it consistently outperforms established baselines. Our method yields up to 35% AUROC gains in neural signal decoding (BrainTreeBank), 16% RMSE reductions in skin temperature prediction (DREAMT), and over 20% improvement in accuracy and macro-F1 on SleepEDF under low-data regimes. These results highlight FGNO's robustness to data scarcity and its superior capacity to learn expressive representations for diverse time series.

Decoupled Diffusion Sampling for Inverse Problems on Function Spaces

We propose a data-efficient, physics-aware generative framework in function space for inverse PDE problems. Existing plug-and-play diffusion posterior samplers represent physics implicitly through joint coefficient-solution modeling, requiring substantial paired supervision. In contrast, our Decoupled Diffusion Inverse Solver (DDIS) employs a decoupled design: an unconditional diffusion learns the coefficient prior, while a neural operator explicitly models the forward PDE for guidance. This decoupling enables superior data efficiency and effective physics-informed learning, while naturally supporting Decoupled Annealing Posterior Sampling (DAPS) to avoid over-smoothing in Diffusion Posterior Sampling (DPS). Theoretically, we prove that DDIS avoids the guidance attenuation failure of joint models when training data is scarce. Empirically, DDIS achieves state-of-the-art performance under sparse observation, improving $l_2$ error by 11% and spectral error by 54% on average; when data is limited to 1%, DDIS maintains accuracy with 40% advantage in $l_2$ error compared to joint models.

Transition Matching Distillation for Fast Video Generation

Large video diffusion and flow models have achieved remarkable success in high-quality video generation, but their use in real-time interactive applications remains limited due to their inefficient multi-step sampling process. In this work, we present Transition Matching Distillation (TMD), a novel framework for distilling video diffusion models into efficient few-step generators. The central idea of TMD is to match the multi-step denoising trajectory of a diffusion model with a few-step probability transition process, where each transition is modeled as a lightweight conditional flow. To enable efficient distillation, we decompose the original diffusion backbone into two components: (1) a main backbone, comprising the majority of early layers, that extracts semantic representations at each outer transition step; and (2) a flow head, consisting of the last few layers, that leverages these representations to perform multiple inner flow updates. Given a pretrained video diffusion model, we first introduce a flow head to the model, and adapt it into a conditional flow map. We then apply distribution matching distillation to the student model with flow head rollout in each transition step. Extensive experiments on distilling Wan2.1 1.3B and 14B text-to-video models demonstrate that TMD provides a flexible and strong trade-off between generation speed and visual quality. In particular, TMD outperforms existing distilled models under comparable inference costs in terms of visual fidelity and prompt adherence. Project page: https://research.nvidia.com/labs/genair/tmd

Advancing End-to-End Pixel Space Generative Modeling via Self-supervised Pre-training

Pixel-space generative models are often more difficult to train and generally underperform compared to their latent-space counterparts, leaving a persistent performance and efficiency gap. In this paper, we introduce a novel two-stage training framework that closes this gap for pixel-space diffusion and consistency models. In the first stage, we pre-train encoders to capture meaningful semantics from clean images while aligning them with points along the same deterministic sampling trajectory, which evolves points from the prior to the data distribution. In the second stage, we integrate the encoder with a randomly initialized decoder and fine-tune the complete model end-to-end for both diffusion and consistency models. Our training framework demonstrates strong empirical performance on ImageNet dataset. Specifically, our diffusion model reaches an FID of 2.04 on ImageNet-256 and 2.35 on ImageNet-512 with 75 number of function evaluations (NFE), surpassing prior pixel-space methods by a large margin in both generation quality and efficiency while rivaling leading VAE-based models at comparable training cost. Furthermore, on ImageNet-256, our consistency model achieves an impressive FID of 8.82 in a single sampling step, significantly surpassing its latent-space counterpart. To the best of our knowledge, this marks the first successful training of a consistency model directly on high-resolution images without relying on pre-trained VAEs or diffusion models.

Trust Region Constrained Measure Transport in Path Space for Stochastic Optimal Control and Inference

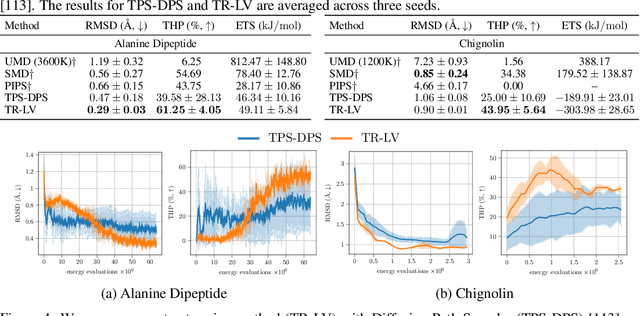
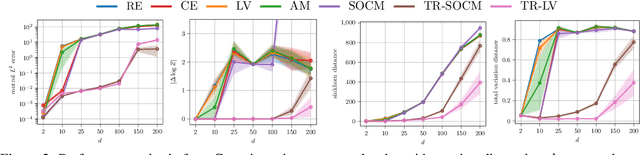
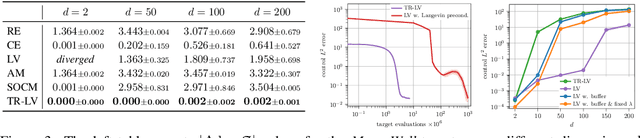
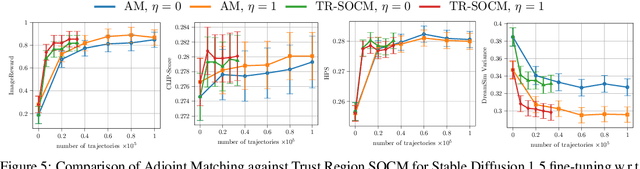
Solving stochastic optimal control problems with quadratic control costs can be viewed as approximating a target path space measure, e.g. via gradient-based optimization. In practice, however, this optimization is challenging in particular if the target measure differs substantially from the prior. In this work, we therefore approach the problem by iteratively solving constrained problems incorporating trust regions that aim for approaching the target measure gradually in a systematic way. It turns out that this trust region based strategy can be understood as a geometric annealing from the prior to the target measure, where, however, the incorporated trust regions lead to a principled and educated way of choosing the time steps in the annealing path. We demonstrate in multiple optimal control applications that our novel method can improve performance significantly, including tasks in diffusion-based sampling, transition path sampling, and fine-tuning of diffusion models.

Principled Approaches for Extending Neural Architectures to Function Spaces for Operator Learning

A wide range of scientific problems, such as those described by continuous-time dynamical systems and partial differential equations (PDEs), are naturally formulated on function spaces. While function spaces are typically infinite-dimensional, deep learning has predominantly advanced through applications in computer vision and natural language processing that focus on mappings between finite-dimensional spaces. Such fundamental disparities in the nature of the data have limited neural networks from achieving a comparable level of success in scientific applications as seen in other fields. Neural operators are a principled way to generalize neural networks to mappings between function spaces, offering a pathway to replicate deep learning's transformative impact on scientific problems. For instance, neural operators can learn solution operators for entire classes of PDEs, e.g., physical systems with different boundary conditions, coefficient functions, and geometries. A key factor in deep learning's success has been the careful engineering of neural architectures through extensive empirical testing. Translating these neural architectures into neural operators allows operator learning to enjoy these same empirical optimizations. However, prior neural operator architectures have often been introduced as standalone models, not directly derived as extensions of existing neural network architectures. In this paper, we identify and distill the key principles for constructing practical implementations of mappings between infinite-dimensional function spaces. Using these principles, we propose a recipe for converting several popular neural architectures into neural operators with minimal modifications. This paper aims to guide practitioners through this process and details the steps to make neural operators work in practice. Our code can be found at https://github.com/neuraloperator/NNs-to-NOs

Guided Diffusion Sampling on Function Spaces with Applications to PDEs

We propose a general framework for conditional sampling in PDE-based inverse problems, targeting the recovery of whole solutions from extremely sparse or noisy measurements. This is accomplished by a function-space diffusion model and plug-and-play guidance for conditioning. Our method first trains an unconditional discretization-agnostic denoising model using neural operator architectures. At inference, we refine the samples to satisfy sparse observation data via a gradient-based guidance mechanism. Through rigorous mathematical analysis, we extend Tweedie's formula to infinite-dimensional Hilbert spaces, providing the theoretical foundation for our posterior sampling approach. Our method (FunDPS) accurately captures posterior distributions in function spaces under minimal supervision and severe data scarcity. Across five PDE tasks with only 3% observation, our method achieves an average 32% accuracy improvement over state-of-the-art fixed-resolution diffusion baselines while reducing sampling steps by 4x. Furthermore, multi-resolution fine-tuning ensures strong cross-resolution generalizability. To the best of our knowledge, this is the first diffusion-based framework to operate independently of discretization, offering a practical and flexible solution for forward and inverse problems in the context of PDEs. Code is available at https://github.com/neuraloperator/FunDPS