Fourier Neural Operators for Learning Dynamics in Quantum Spin Systems

Fourier Neural Operators (FNOs) excel on tasks using functional data, such as those originating from partial differential equations. Such characteristics render them an effective approach for simulating the time evolution of quantum wavefunctions, which is a computationally challenging, yet coveted task for understanding quantum systems. In this manuscript, we use FNOs to model the evolution of random quantum spin systems, so chosen due to their representative quantum dynamics and minimal symmetry. We explore two distinct FNO architectures and examine their performance for learning and predicting time evolution using both random and low-energy input states. Additionally, we apply FNOs to a compact set of Hamiltonian observables ($\sim\text{poly}(n)$) instead of the entire $2^n$ quantum wavefunction, which greatly reduces the size of our inputs and outputs and, consequently, the requisite dimensions of the resulting FNOs. Moreover, this Hamiltonian observable-based method demonstrates that FNOs can effectively distill information from high-dimensional spaces into lower-dimensional spaces. The extrapolation of Hamiltonian observables to times later than those used in training is of particular interest, as this stands to fundamentally increase the simulatability of quantum systems past both the coherence times of contemporary quantum architectures and the circuit-depths of tractable tensor networks.

A Neural Network Solves and Generates Mathematics Problems by Program Synthesis: Calculus, Differential Equations, Linear Algebra, and More

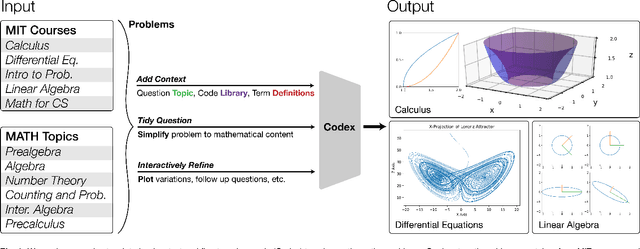
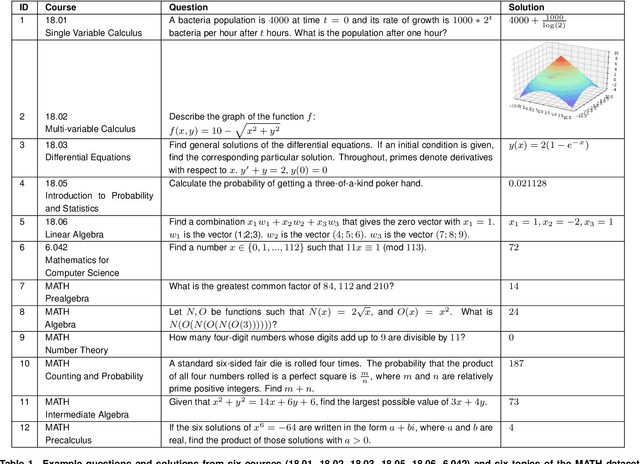
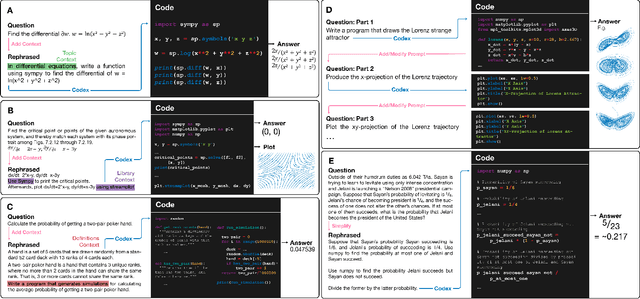
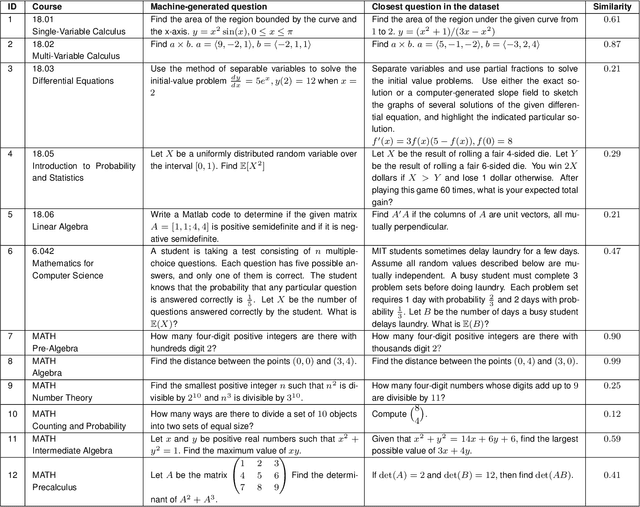
We demonstrate that a neural network pre-trained on text and fine-tuned on code solves Mathematics problems by program synthesis. We turn questions into programming tasks, automatically generate programs, and then execute them, perfectly solving university-level problems from MIT's large Mathematics courses (Single Variable Calculus 18.01, Multivariable Calculus 18.02, Differential Equations 18.03, Introduction to Probability and Statistics 18.05, Linear Algebra 18.06, and Mathematics for Computer Science 6.042), Columbia University's COMS3251 Computational Linear Algebra course, as well as questions from a MATH dataset (on Prealgebra, Algebra, Counting and Probability, Number Theory, and Precalculus), the latest benchmark of advanced mathematics problems specifically designed to assess mathematical reasoning. We explore prompt generation methods that enable Transformers to generate question solving programs for these subjects, including solutions with plots. We generate correct answers for a random sample of questions in each topic. We quantify the gap between the original and transformed questions and perform a survey to evaluate the quality and difficulty of generated questions. This is the first work to automatically solve, grade, and generate university-level Mathematics course questions at scale. This represents a milestone for higher education.